Revisiting Incremental Stochastic Majorization-Minimization Algorithms with Applications to Mixture of Experts

Processing high-volume, streaming data is increasingly common in modern statistics and machine learning, where batch-mode algorithms are often impractical because they require repeated passes over the full dataset. This has motivated incremental stochastic estimation methods, including the incremental stochastic Expectation-Maximization (EM) algorithm formulated via stochastic approximation. In this work, we revisit and analyze an incremental stochastic variant of the Majorization-Minimization (MM) algorithm, which generalizes incremental stochastic EM as a special case. Our approach relaxes key EM requirements, such as explicit latent-variable representations, enabling broader applicability and greater algorithmic flexibility. We establish theoretical guarantees for the incremental stochastic MM algorithm, proving consistency in the sense that the iterates converge to a stationary point characterized by a vanishing gradient of the objective. We demonstrate these advantages on a softmax-gated mixture of experts (MoE) regression problem, for which no stochastic EM algorithm is available. Empirically, our method consistently outperforms widely used stochastic optimizers, including stochastic gradient descent, root mean square propagation, adaptive moment estimation, and second-order clipped stochastic optimization. These results support the development of new incremental stochastic algorithms, given the central role of softmax-gated MoE architectures in contemporary deep neural networks for heterogeneous data modeling. Beyond synthetic experiments, we also validate practical effectiveness on two real-world datasets, including a bioinformatics study of dent maize genotypes under drought stress that integrates high-dimensional proteomics with ecophysiological traits, where incremental stochastic MM yields stable gains in predictive performance.

MMP-A*: Multimodal Perception Enhanced Incremental Heuristic Search on Path Planning

Autonomous path planning requires a synergy between global reasoning and geometric precision, especially in complex or cluttered environments. While classical A* is valued for its optimality, it incurs prohibitive computational and memory costs in large-scale scenarios. Recent attempts to mitigate these limitations by using Large Language Models for waypoint guidance remain insufficient, as they rely only on text-based reasoning without spatial grounding. As a result, such models often produce incorrect waypoints in topologically complex environments with dead ends, and lack the perceptual capacity to interpret ambiguous physical boundaries. These inconsistencies lead to costly corrective expansions and undermine the intended computational efficiency. We introduce MMP-A*, a multimodal framework that integrates the spatial grounding capabilities of vision-language models with a novel adaptive decay mechanism. By anchoring high-level reasoning in physical geometry, the framework produces coherent waypoint guidance that addresses the limitations of text-only planners. The adaptive decay mechanism dynamically regulates the influence of uncertain waypoints within the heuristic, ensuring geometric validity while substantially reducing memory overhead. To evaluate robustness, we test the framework in challenging environments characterized by severe clutter and topological complexity. Experimental results show that MMP-A* achieves near-optimal trajectories with significantly reduced operational costs, demonstrating its potential as a perception-grounded and computationally efficient paradigm for autonomous navigation.

Kernel Clustering with Sigmoid-based Regularization for Efficient Segmentation of Sequential Data

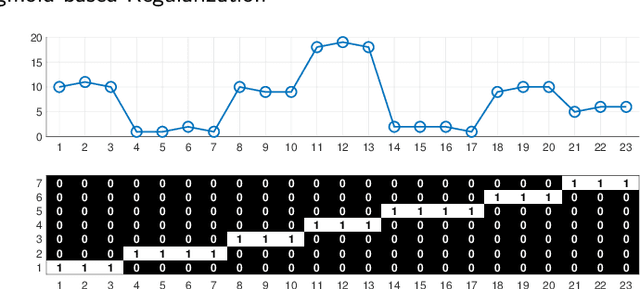
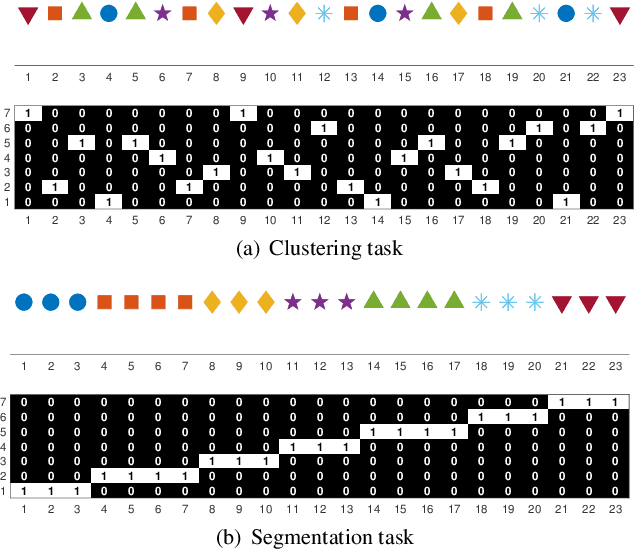
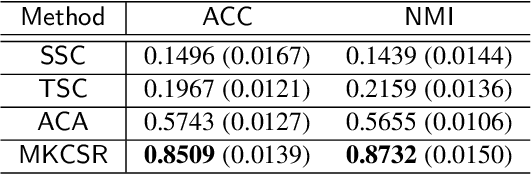
Kernel segmentation aims at partitioning a data sequence into several non-overlapping segments that may have nonlinear and complex structures. In general, it is formulated as a discrete optimization problem with combinatorial constraints. A popular algorithm for optimally solving this problem is dynamic programming (DP), which has quadratic computation and memory requirements. Given that sequences in practice are too long, this algorithm is not a practical approach. Although many heuristic algorithms have been proposed to approximate the optimal segmentation, they have no guarantee on the quality of their solutions. In this paper, we take a differentiable approach to alleviate the aforementioned issues. First, we introduce a novel sigmoid-based regularization to smoothly approximate the combinatorial constraints. Combining it with objective of the balanced kernel clustering, we formulate a differentiable model termed Kernel clustering with sigmoid-based regularization (KCSR), where the gradient-based algorithm can be exploited to obtain the optimal segmentation. Second, we develop a stochastic variant of the proposed model. By using the stochastic gradient descent algorithm, which has much lower time and space complexities, for optimization, the second model can perform segmentation on overlong data sequences. Finally, for simultaneously segmenting multiple data sequences, we slightly modify the sigmoid-based regularization to further introduce an extended variant of the proposed model. Through extensive experiments on various types of data sequences performances of our models are evaluated and compared with those of the existing methods. The experimental results validate advantages of the proposed models. Our Matlab source code is available on github.

Guaranteed inference in topic models

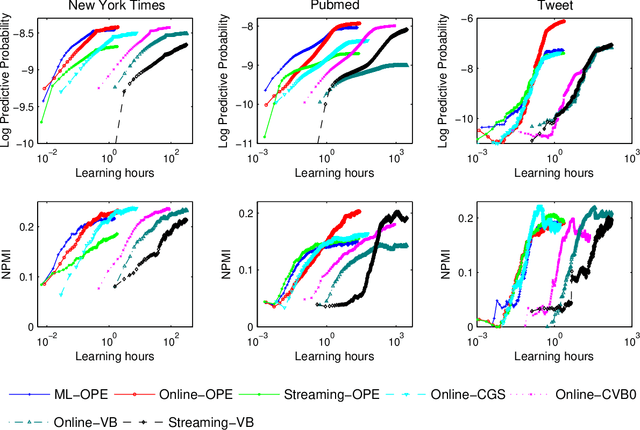
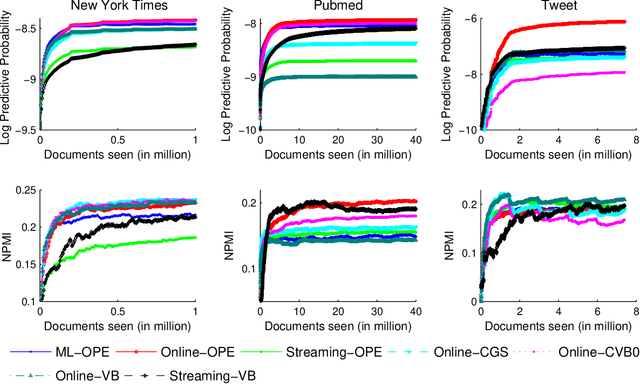
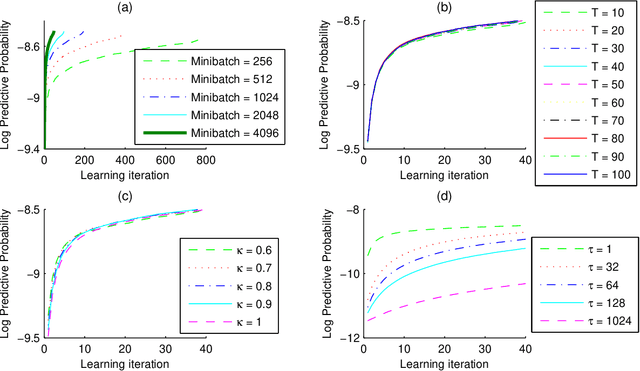
One of the core problems in statistical models is the estimation of a posterior distribution. For topic models, the problem of posterior inference for individual texts is particularly important, especially when dealing with data streams, but is often intractable in the worst case. As a consequence, existing methods for posterior inference are approximate and do not have any guarantee on neither quality nor convergence rate. In this paper, we introduce a provably fast algorithm, namely Online Maximum a Posteriori Estimation (OPE), for posterior inference in topic models. OPE has more attractive properties than existing inference approaches, including theoretical guarantees on quality and fast rate of convergence to a local maximal/stationary point of the inference problem. The discussions about OPE are very general and hence can be easily employed in a wide range of contexts. Finally, we employ OPE to design three methods for learning Latent Dirichlet Allocation from text streams or large corpora. Extensive experiments demonstrate some superior behaviors of OPE and of our new learning methods.