Soft-Bayes: Prod for Mixtures of Experts with Log-Loss

We consider prediction with expert advice under the log-loss with the goal of deriving efficient and robust algorithms. We argue that existing algorithms such as exponentiated gradient, online gradient descent and online Newton step do not adequately satisfy both requirements. Our main contribution is an analysis of the Prod algorithm that is robust to any data sequence and runs in linear time relative to the number of experts in each round. Despite the unbounded nature of the log-loss, we derive a bound that is independent of the largest loss and of the largest gradient, and depends only on the number of experts and the time horizon. Furthermore we give a Bayesian interpretation of Prod and adapt the algorithm to derive a tracking regret.

Single-Agent Policy Tree Search With Guarantees

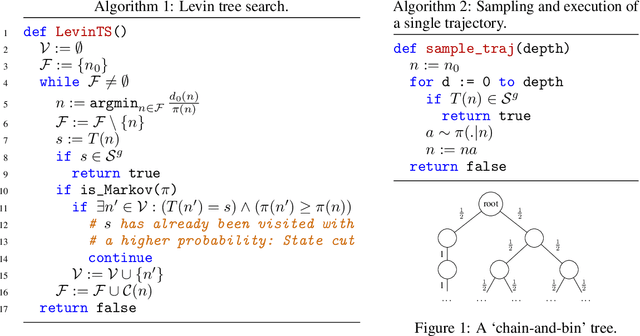
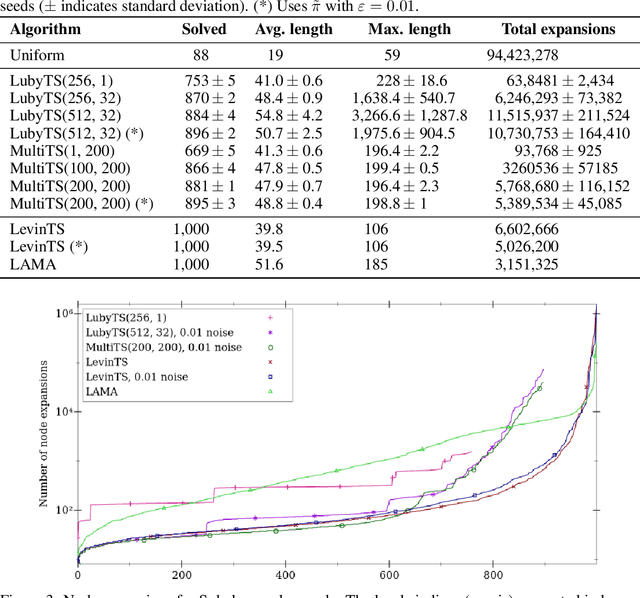
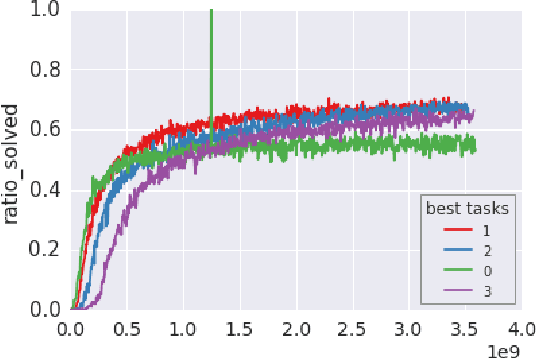
We introduce two novel tree search algorithms that use a policy to guide search. The first algorithm is a best-first enumeration that uses a cost function that allows us to prove an upper bound on the number of nodes to be expanded before reaching a goal state. We show that this best-first algorithm is particularly well suited for `needle-in-a-haystack' problems. The second algorithm is based on sampling and we prove an upper bound on the expected number of nodes it expands before reaching a set of goal states. We show that this algorithm is better suited for problems where many paths lead to a goal. We validate these tree search algorithms on 1,000 computer-generated levels of Sokoban, where the policy used to guide the search comes from a neural network trained using A3C. Our results show that the policy tree search algorithms we introduce are competitive with a state-of-the-art domain-independent planner that uses heuristic search.

Garbage In, Reward Out: Bootstrapping Exploration in Multi-Armed Bandits

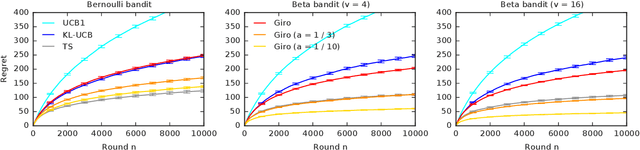
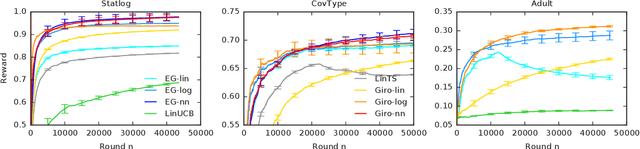
We propose a multi-armed bandit algorithm that explores based on randomizing its history. The key idea is to estimate the value of the arm from the bootstrap sample of its history, where we add pseudo observations after each pull of the arm. The pseudo observations seem to be harmful. But on the contrary, they guarantee that the bootstrap sample is optimistic with a high probability. Because of this, we call our algorithm Giro, which is an abbreviation for garbage in, reward out. We analyze Giro in a $K$-armed Bernoulli bandit and prove a $O(K \Delta^{-1} \log n)$ bound on its $n$-round regret, where $\Delta$ denotes the difference in the expected rewards of the optimal and best suboptimal arms. The main advantage of our exploration strategy is that it can be applied to any reward function generalization, such as neural networks. We evaluate Giro and its contextual variant on multiple synthetic and real-world problems, and observe that Giro is comparable to or better than state-of-the-art algorithms.

BubbleRank: Safe Online Learning to Rerank

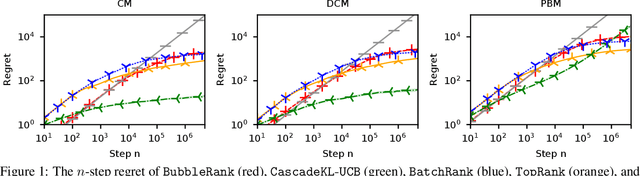
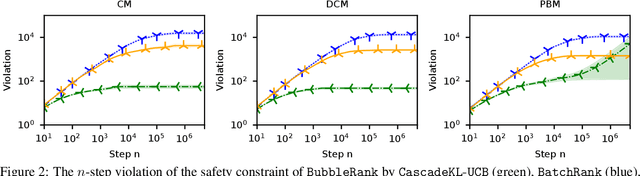
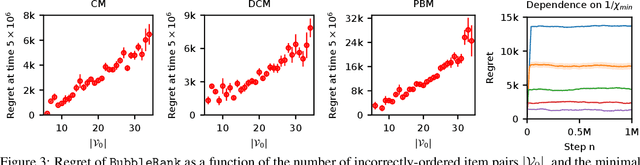
We study the problem of online learning to re-rank, where users provide feedback to improve the quality of displayed lists. Learning to rank has been traditionally studied in two settings. In the offline setting, rankers are typically learned from relevance labels of judges. These approaches have become the industry standard. However, they lack exploration, and thus are limited by the information content of offline data. In the online setting, an algorithm can propose a list and learn from the feedback on it in a sequential fashion. Bandit algorithms developed for this setting actively experiment, and in this way overcome the biases of offline data. But they also tend to ignore offline data, which results in a high initial cost of exploration. We propose BubbleRank, a bandit algorithm for re-ranking that combines the strengths of both settings. The algorithm starts with an initial base list and improves it gradually by swapping higher-ranked less attractive items for lower-ranked more attractive items. We prove an upper bound on the n-step regret of BubbleRank that degrades gracefully with the quality of the initial base list. Our theoretical findings are supported by extensive numerical experiments on a large real-world click dataset.

TopRank: A practical algorithm for online stochastic ranking

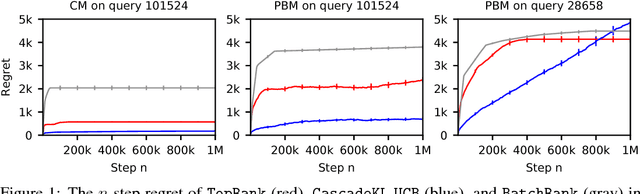
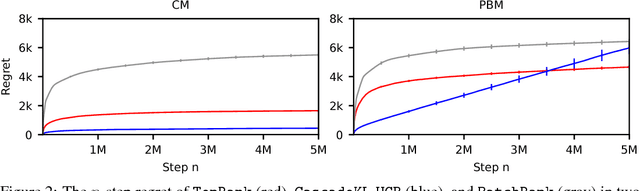
Online learning to rank is a sequential decision-making problem where in each round the learning agent chooses a list of items and receives feedback in the form of clicks from the user. Many sample-efficient algorithms have been proposed for this problem that assume a specific click model connecting rankings and user behavior. We propose a generalized click model that encompasses many existing models, including the position-based and cascade models. Our generalization motivates a novel online learning algorithm based on topological sort, which we call TopRank. TopRank is (a) more natural than existing algorithms, (b) has stronger regret guarantees than existing algorithms with comparable generality, (c) has a more insightful proof that leaves the door open to many generalizations, (d) outperforms existing algorithms empirically.

Cleaning up the neighborhood: A full classification for adversarial partial monitoring

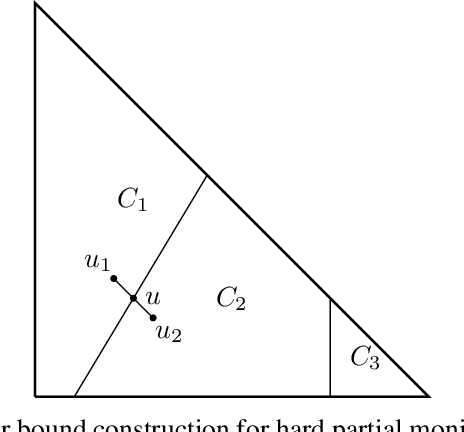
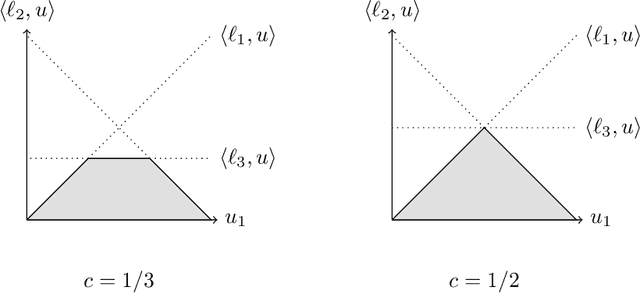
Partial monitoring is a generalization of the well-known multi-armed bandit framework where the loss is not directly observed by the learner. We complete the classification of finite adversarial partial monitoring to include all games, solving an open problem posed by Bartok et al. [2014]. Along the way we simplify and improve existing algorithms and correct errors in previous analyses. Our second contribution is a new algorithm for the class of games studied by Bartok [2013] where we prove upper and lower regret bounds that shed more light on the dependence of the regret on the game structure.

Unifying PAC and Regret: Uniform PAC Bounds for Episodic Reinforcement Learning

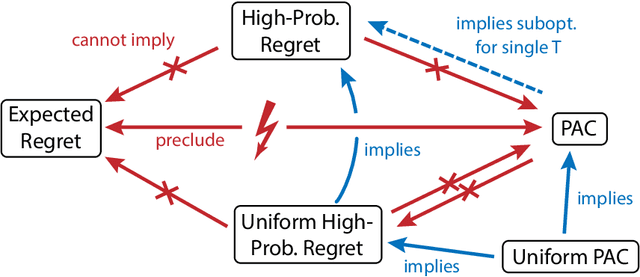
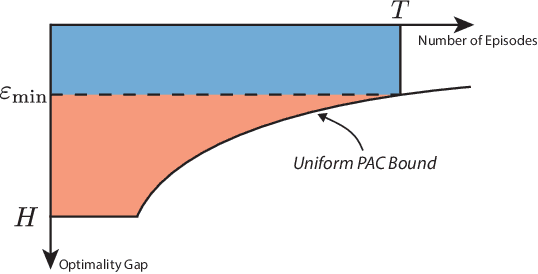
Statistical performance bounds for reinforcement learning (RL) algorithms can be critical for high-stakes applications like healthcare. This paper introduces a new framework for theoretically measuring the performance of such algorithms called Uniform-PAC, which is a strengthening of the classical Probably Approximately Correct (PAC) framework. In contrast to the PAC framework, the uniform version may be used to derive high probability regret guarantees and so forms a bridge between the two setups that has been missing in the literature. We demonstrate the benefits of the new framework for finite-state episodic MDPs with a new algorithm that is Uniform-PAC and simultaneously achieves optimal regret and PAC guarantees except for a factor of the horizon.

Online Learning with Gated Linear Networks

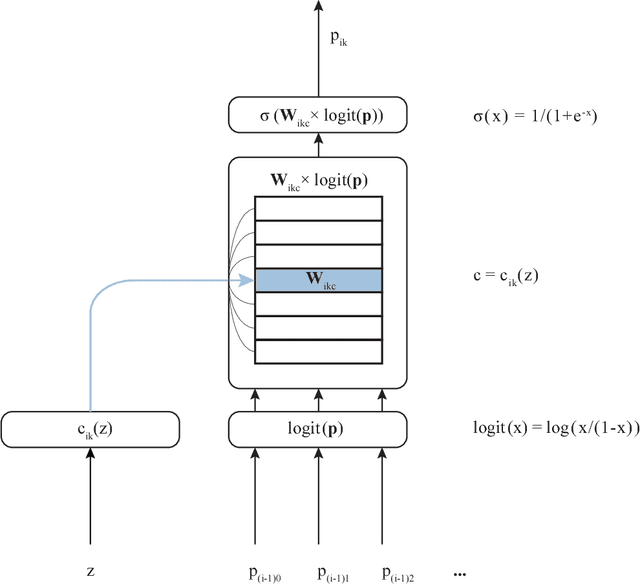
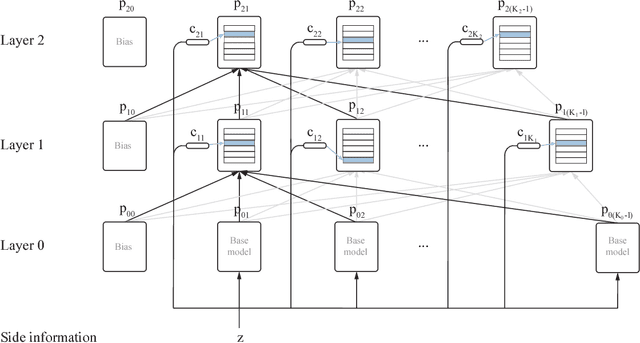
This paper describes a family of probabilistic architectures designed for online learning under the logarithmic loss. Rather than relying on non-linear transfer functions, our method gains representational power by the use of data conditioning. We state under general conditions a learnable capacity theorem that shows this approach can in principle learn any bounded Borel-measurable function on a compact subset of euclidean space; the result is stronger than many universality results for connectionist architectures because we provide both the model and the learning procedure for which convergence is guaranteed.

A Scale Free Algorithm for Stochastic Bandits with Bounded Kurtosis

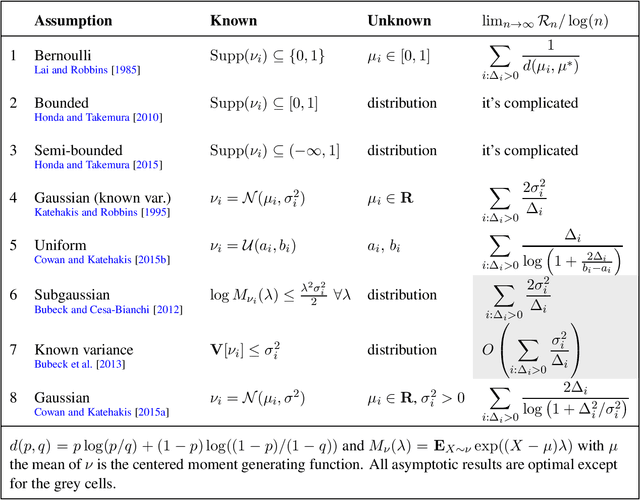
Existing strategies for finite-armed stochastic bandits mostly depend on a parameter of scale that must be known in advance. Sometimes this is in the form of a bound on the payoffs, or the knowledge of a variance or subgaussian parameter. The notable exceptions are the analysis of Gaussian bandits with unknown mean and variance by Cowan and Katehakis [2015] and of uniform distributions with unknown support [Cowan and Katehakis, 2015]. The results derived in these specialised cases are generalised here to the non-parametric setup, where the learner knows only a bound on the kurtosis of the noise, which is a scale free measure of the extremity of outliers.

Refined Lower Bounds for Adversarial Bandits

We provide new lower bounds on the regret that must be suffered by adversarial bandit algorithms. The new results show that recent upper bounds that either (a) hold with high-probability or (b) depend on the total lossof the best arm or (c) depend on the quadratic variation of the losses, are close to tight. Besides this we prove two impossibility results. First, the existence of a single arm that is optimal in every round cannot improve the regret in the worst case. Second, the regret cannot scale with the effective range of the losses. In contrast, both results are possible in the full-information setting.