MCMC Variational Inference via Uncorrected Hamiltonian Annealing

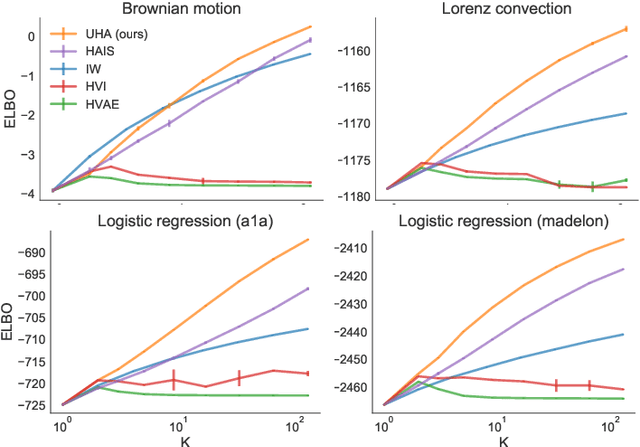
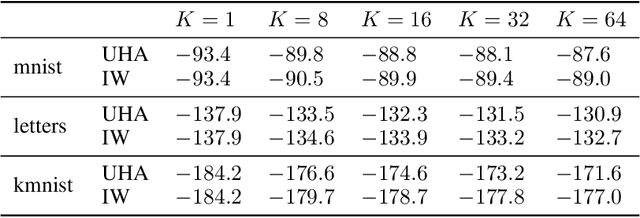
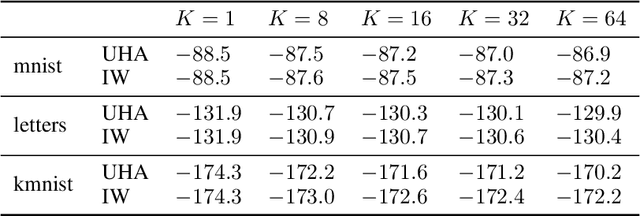
Given an unnormalized target distribution we want to obtain approximate samples from it and a tight lower bound on its (log) normalization constant log Z. Annealed Importance Sampling (AIS) with Hamiltonian MCMC is a powerful method that can be used to do this. Its main drawback is that it uses non-differentiable transition kernels, which makes tuning its many parameters hard. We propose a framework to use an AIS-like procedure with Uncorrected Hamiltonian MCMC, called Uncorrected Hamiltonian Annealing. Our method leads to tight and differentiable lower bounds on log Z. We show empirically that our method yields better performances than other competing approaches, and that the ability to tune its parameters using reparameterization gradients may lead to large performance improvements.

Empirical Evaluation of Biased Methods for Alpha Divergence Minimization

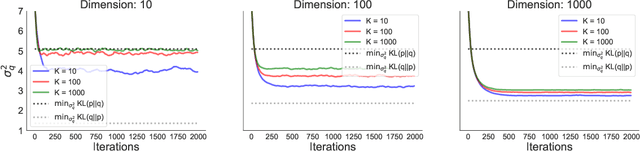
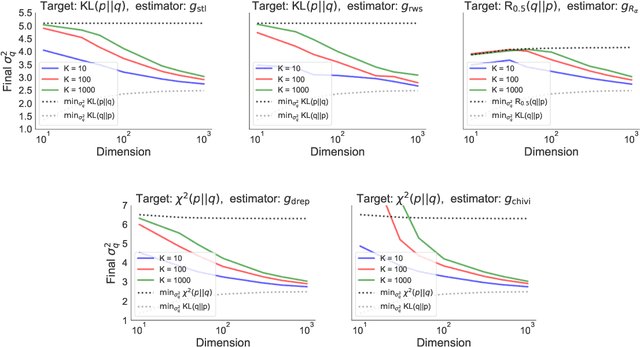
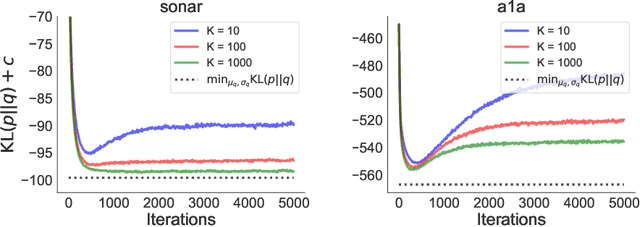
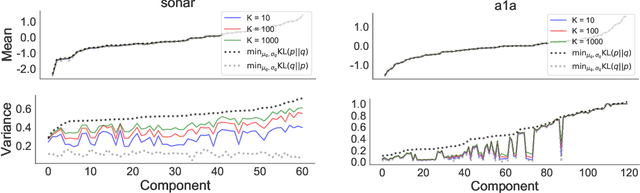
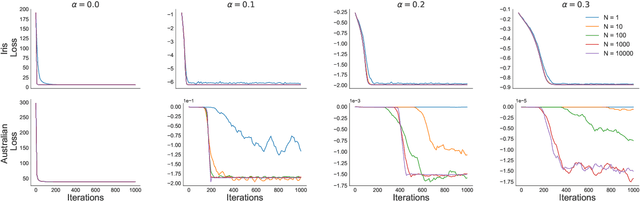
In this paper we empirically evaluate biased methods for alpha-divergence minimization. In particular, we focus on how the bias affects the final solutions found, and how this depends on the dimensionality of the problem. We find that (i) solutions returned by these methods appear to be strongly biased towards minimizers of the traditional "exclusive" KL-divergence, KL(q||p), and (ii) in high dimensions, an impractically large amount of computation is needed to mitigate this bias and obtain solutions that actually minimize the alpha-divergence of interest.

On the Difficulty of Unbiased Alpha Divergence Minimization

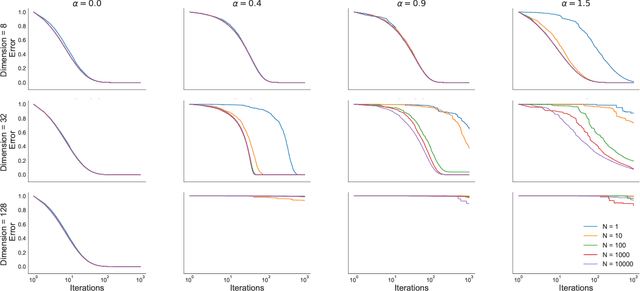
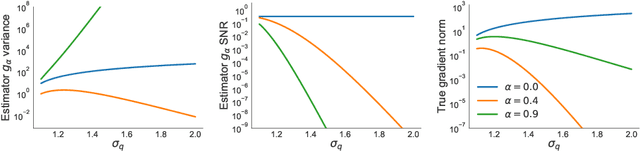
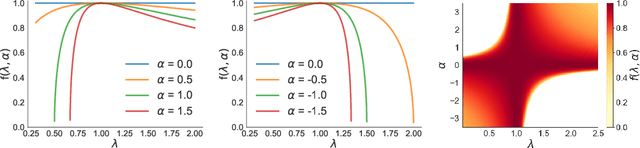
Several approximate inference algorithms have been proposed to minimize an alpha-divergence between an approximating distribution and a target distribution. Many of these algorithms introduce bias, the magnitude of which is poorly understood. Other algorithms are unbiased. These often seem to suffer from high variance, but again, little is rigorously known. In this work we study unbiased methods for alpha-divergence minimization through the Signal-to-Noise Ratio (SNR) of the gradient estimator. We study several representative scenarios where strong analytical results are possible, such as fully-factorized or Gaussian distributions. We find that when alpha is not zero, the SNR worsens exponentially in the dimensionality of the problem. This casts doubt on the practicality of these methods. We empirically confirm these theoretical results.

Approximation Based Variance Reduction for Reparameterization Gradients

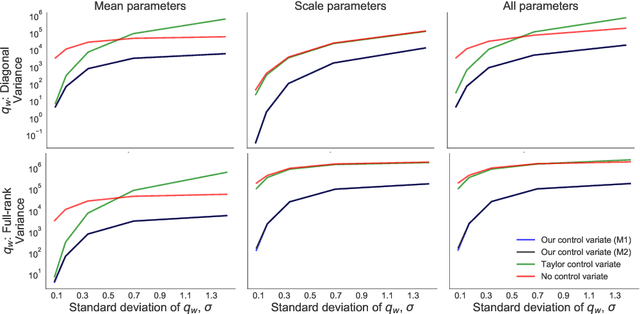
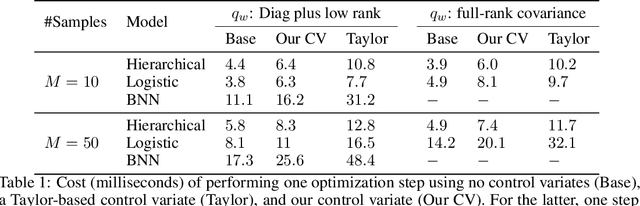
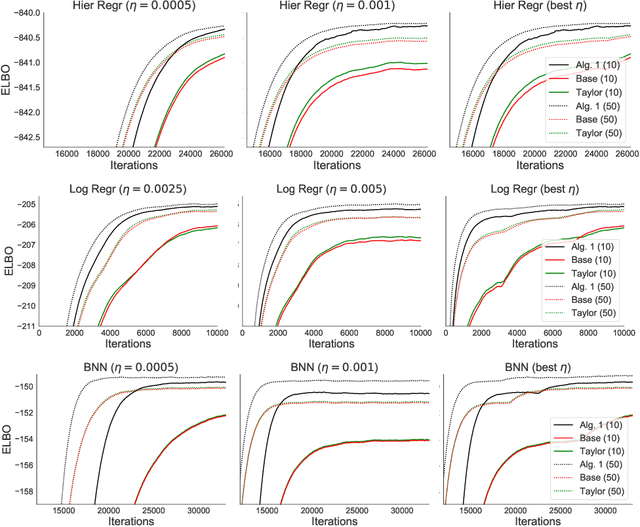
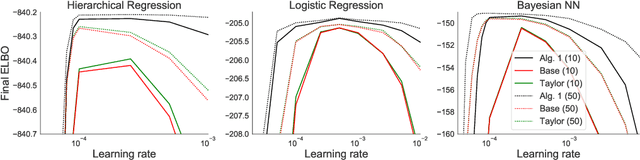
Flexible variational distributions improve variational inference but are harder to optimize. In this work we present a control variate that is applicable for any reparameterizable distribution with known mean and covariance matrix, e.g. Gaussians with any covariance structure. The control variate is based on a quadratic approximation of the model, and its parameters are set using a double-descent scheme by minimizing the gradient estimator's variance. We empirically show that this control variate leads to large improvements in gradient variance and optimization convergence for inference with non-factorized variational distributions.

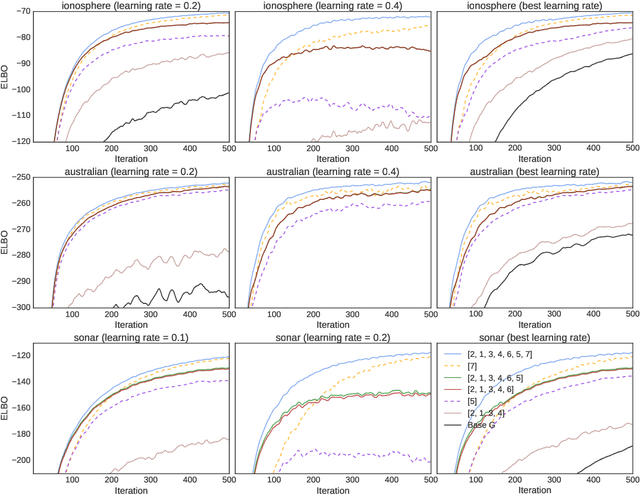
A Rule for Gradient Estimator Selection, with an Application to Variational Inference

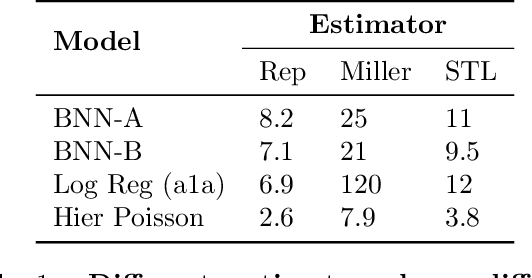
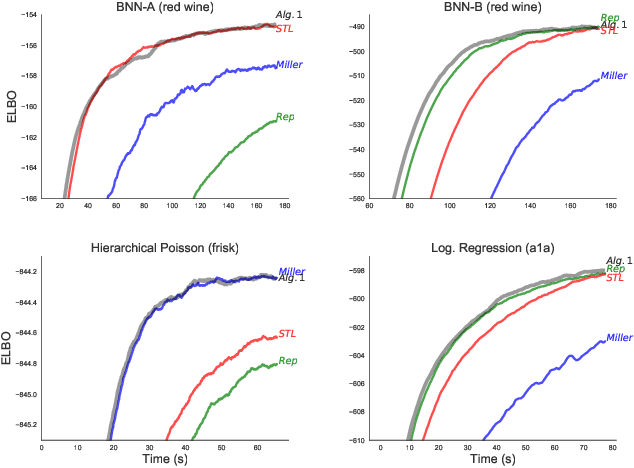
Stochastic gradient descent (SGD) is the workhorse of modern machine learning. Sometimes, there are many different potential gradient estimators that can be used. When so, choosing the one with the best tradeoff between cost and variance is important. This paper analyzes the convergence rates of SGD as a function of time, rather than iterations. This results in a simple rule to select the estimator that leads to the best optimization convergence guarantee. This choice is the same for different variants of SGD, and with different assumptions about the objective (e.g. convexity or smoothness). Inspired by this principle, we propose a technique to automatically select an estimator when a finite pool of estimators is given. Then, we extend to infinite pools of estimators, where each one is indexed by control variate weights. This is enabled by a reduction to a mixed-integer quadratic program. Empirically, automatically choosing an estimator performs comparably to the best estimator chosen with hindsight.

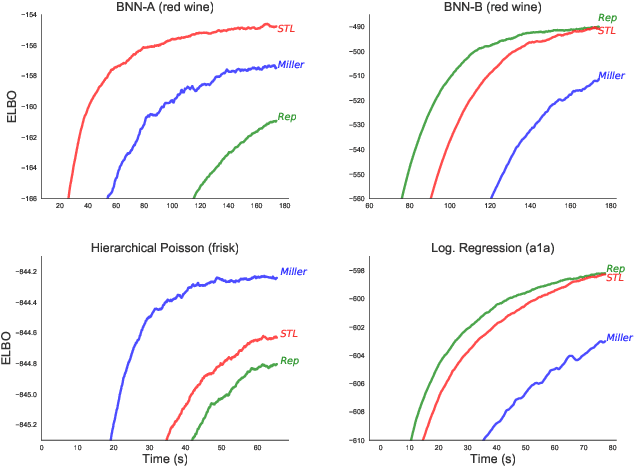
Using Large Ensembles of Control Variates for Variational Inference

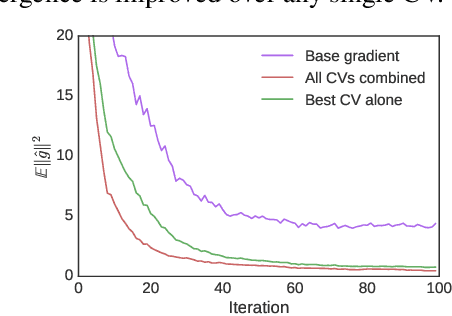
Variational inference is increasingly being addressed with stochastic optimization. In this setting, the gradient's variance plays a crucial role in the optimization procedure, since high variance gradients lead to poor convergence. A popular approach used to reduce gradient's variance involves the use of control variates. Despite the good results obtained, control variates developed for variational inference are typically looked at in isolation. In this paper we clarify the large number of control variates that are available by giving a systematic view of how they are derived. We also present a Bayesian risk minimization framework in which the quality of a procedure for combining control variates is quantified by its effect on optimization convergence rates, which leads to a very simple combination rule. Results show that combining a large number of control variates this way significantly improves the convergence of inference over using the typical gradient estimators or a reduced number of control variates.

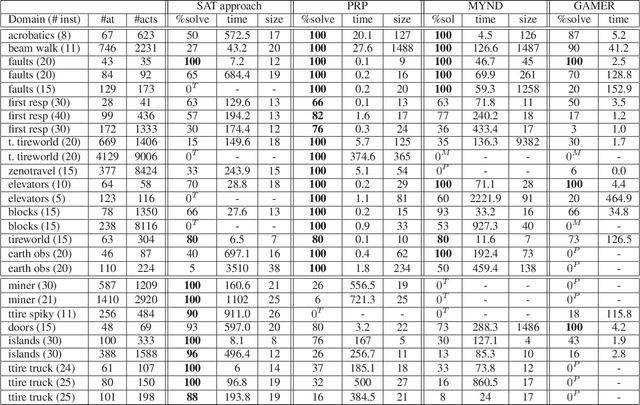
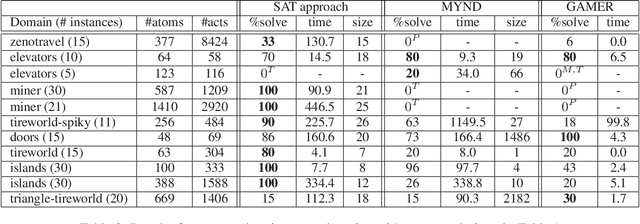
Compact Policies for Fully-Observable Non-Deterministic Planning as SAT

Fully observable non-deterministic (FOND) planning is becoming increasingly important as an approach for computing proper policies in probabilistic planning, extended temporal plans in LTL planning, and general plans in generalized planning. In this work, we introduce a SAT encoding for FOND planning that is compact and can produce compact strong cyclic policies. Simple variations of the encodings are also introduced for strong planning and for what we call, dual FOND planning, where some non-deterministic actions are assumed to be fair (e.g., probabilistic) and others unfair (e.g., adversarial). The resulting FOND planners are compared empirically with existing planners over existing and new benchmarks. The notion of "probabilistic interesting problems" is also revisited to yield a more comprehensive picture of the strengths and limitations of current FOND planners and the proposed SAT approach.