Learning vertical coordinates via automatic differentiation of a dynamical core

Terrain-following coordinates in atmospheric models often imprint their grid structure onto the solution, particularly over steep topography, where distorted coordinate layers can generate spurious horizontal and vertical motion. Standard formulations, such as hybrid or SLEVE coordinates, mitigate these errors by using analytic decay functions controlled by heuristic scale parameters that are typically tuned by hand and fixed a priori. In this work, we propose a framework to define a parametric vertical coordinate system as a learnable component within a differentiable dynamical core. We develop an end-to-end differentiable numerical solver for the two-dimensional non-hydrostatic Euler equations on an Arakawa C-grid, and introduce a NEUral Vertical Enhancement (NEUVE) terrain-following coordinate based on an integral transformed neural network that guarantees monotonicity. A key feature of our approach is the use of automatic differentiation to compute exact geometric metric terms, thereby eliminating truncation errors associated with finite-difference coordinate derivatives. By coupling simulation errors through the time integration to the parameterization, our formulation finds a grid structure optimized for both the underlying physics and numerics. Using several standard tests, we demonstrate that these learned coordinates reduce the mean squared error by a factor of 1.4 to 2 in non-linear statistical benchmarks, and eliminate spurious vertical velocity striations over steep topography.

Pushing the Limits of Extreme Weather: Constructing Extreme Heatwave Storylines with Differentiable Climate Models

Understanding the plausible upper bounds of extreme weather events is essential for risk assessment in a warming climate. Existing methods, based on large ensembles of physics-based models, are often computationally expensive or lack the fidelity needed to simulate rare, high-impact extremes. Here, we present a novel framework that leverages a differentiable hybrid climate model, NeuralGCM, to optimize initial conditions and generate physically consistent worst-case heatwave trajectories. Applied to the 2021 Pacific Northwest heatwave, our method produces temperature anomalies up to 3.7 $^\circ$C above the most extreme member of a 75-member ensemble. These trajectories feature intensified atmospheric blocking and amplified Rossby wave patterns--hallmarks of severe heat events. Our results demonstrate that differentiable climate models can efficiently explore the upper tails of event likelihoods, providing a powerful new approach for constructing targeted storylines of extreme weather under climate change.

Turbulence Scaling from Deep Learning Diffusion Generative Models

Complex spatial and temporal structures are inherent characteristics of turbulent fluid flows and comprehending them poses a major challenge. This comprehesion necessitates an understanding of the space of turbulent fluid flow configurations. We employ a diffusion-based generative model to learn the distribution of turbulent vorticity profiles and generate snapshots of turbulent solutions to the incompressible Navier-Stokes equations. We consider the inverse cascade in two spatial dimensions and generate diverse turbulent solutions that differ from those in the training dataset. We analyze the statistical scaling properties of the new turbulent profiles, calculate their structure functions, energy power spectrum, velocity probability distribution function and moments of local energy dissipation. All the learnt scaling exponents are consistent with the expected Kolmogorov scaling and have lower errors than the training ones. This agreement with established turbulence characteristics provides strong evidence of the model's capability to capture essential features of real-world turbulence.

Neural Network Complexity of Chaos and Turbulence

We study the complexity of chaos and turbulence as viewed by deep neural networks by considering network classification tasks of distinguishing turbulent from chaotic fluid flows, noise and real world images of cats or dogs. We analyze the relative difficulty of these classification tasks and quantify the complexity of the computation at the intermediate and final stages. We analyze incompressible as well as weakly compressible fluid flows and provide evidence for the feature identified by the neural network to distinguish turbulence from chaos.

Using machine learning to parametrize postmerger signals from binary neutron stars

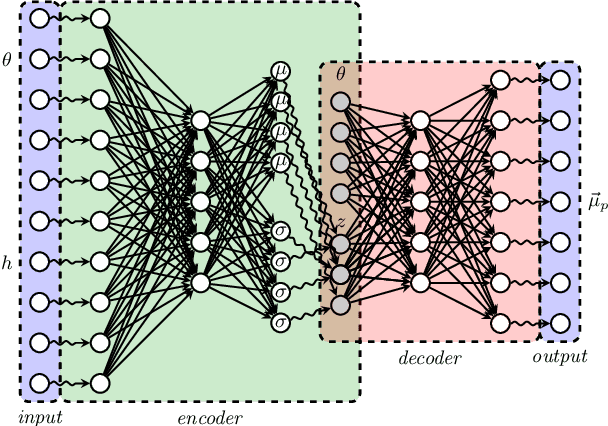
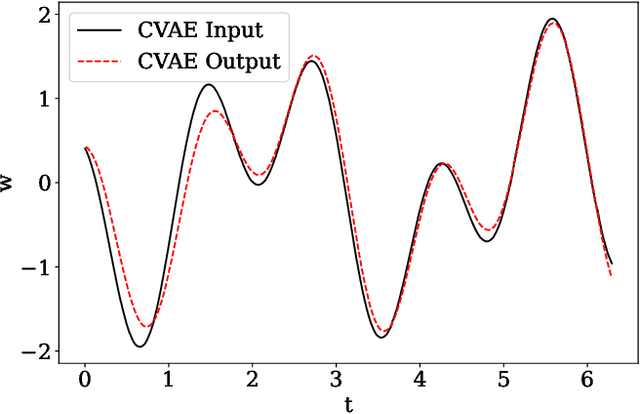
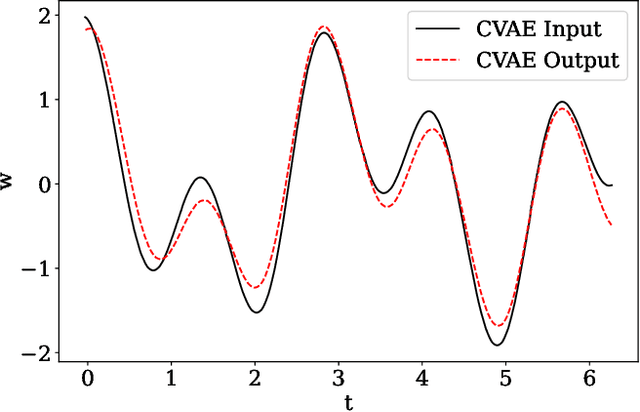
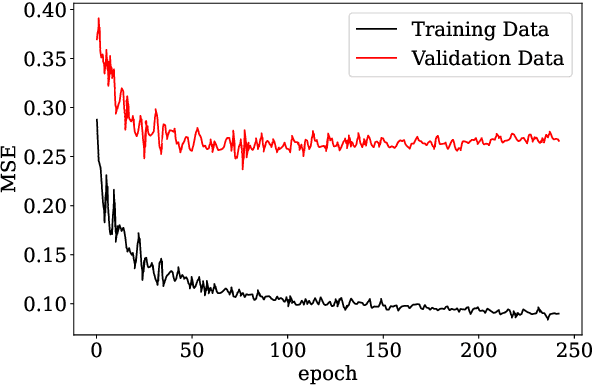
There is growing interest in the detection and characterization of gravitational waves from postmerger oscillations of binary neutron stars. These signals contain information about the nature of the remnant and the high-density and out-of-equilibrium physics of the postmerger processes, which would complement any electromagnetic signal. However, the construction of binary neutron star postmerger waveforms is much more complicated than for binary black holes: (i) there are theoretical uncertainties in the neutron-star equation of state and other aspects of the high-density physics, (ii) numerical simulations are expensive and available ones only cover a small fraction of the parameter space with limited numerical accuracy, and (iii) it is unclear how to parametrize the theoretical uncertainties and interpolate across parameter space. In this work, we describe the use of a machine-learning method called a conditional variational autoencoder (CVAE) to construct postmerger models for hyper/massive neutron star remnant signals based on numerical-relativity simulations. The CVAE provides a probabilistic model, which encodes uncertainties in the training data within a set of latent parameters. We estimate that training such a model will ultimately require $\sim 10^4$ waveforms. However, using synthetic training waveforms as a proof-of-principle, we show that the CVAE can be used as an accurate generative model and that it encodes the equation of state in a useful latent representation.