Permutation Inference for Canonical Correlation Analysis

Canonical correlation analysis (CCA) has become a key tool for population neuroimaging, allowing investigation of associations between many imaging and non-imaging measurements. As age, sex and other variables are often a source of variability not of direct interest, previous work has used CCA on residuals from a model that removes these effects, then proceeded directly to permutation inference. We show that a simple permutation test, as typically used to identify significant modes of shared variation on such data adjusted for nuisance variables, produces inflated error rates. The reason is that residualisation introduces dependencies among the observations that violate the exchangeability assumption. Even in the absence of nuisance variables, however, a simple permutation test for CCA also leads to excess error rates for all canonical correlations other than the first. The reason is that a simple permutation scheme does not ignore the variability already explained by previous canonical variables. Here we propose solutions for both problems: in the case of nuisance variables, we show that transforming the residuals to a lower dimensional basis where exchangeability holds results in a valid permutation test; for more general cases, with or without nuisance variables, we propose estimating the canonical correlations in a stepwise manner, removing at each iteration the variance already explained, while dealing with different number of variables in both sides. We also discuss how to address the multiplicity of tests, proposing an admissible test that is not conservative, and provide a complete algorithm for permutation inference for CCA.

Accelerating Permutation Testing in Voxel-wise Analysis through Subspace Tracking: A new plugin for SnPM

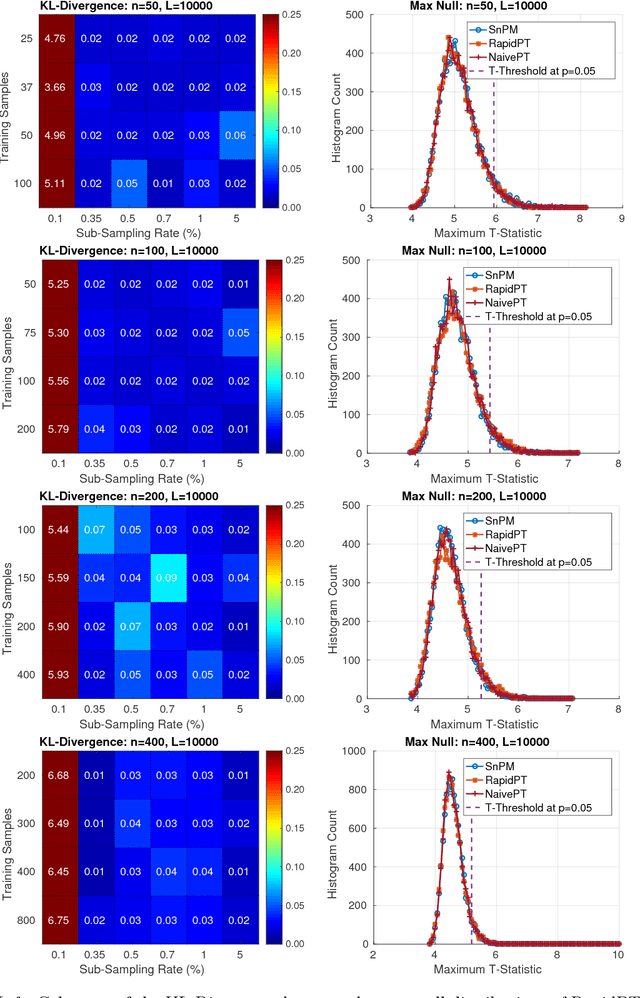
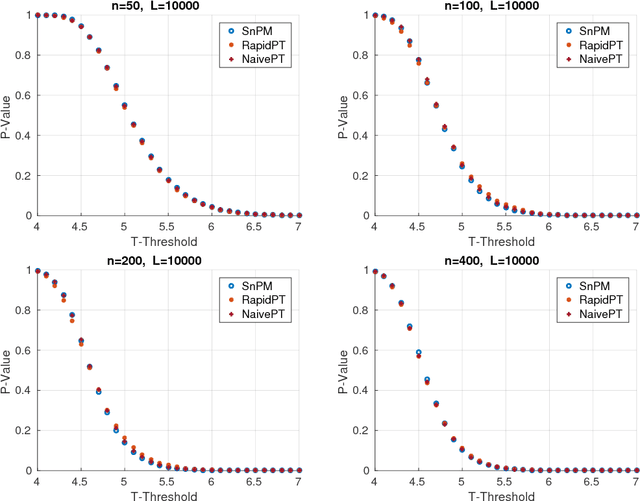
Permutation testing is a non-parametric method for obtaining the max null distribution used to compute corrected $p$-values that provide strong control of false positives. In neuroimaging, however, the computational burden of running such an algorithm can be significant. We find that by viewing the permutation testing procedure as the construction of a very large permutation testing matrix, $T$, one can exploit structural properties derived from the data and the test statistics to reduce the runtime under certain conditions. In particular, we see that $T$ is low-rank plus a low-variance residual. This makes $T$ a good candidate for low-rank matrix completion, where only a very small number of entries of $T$ ($\sim0.35\%$ of all entries in our experiments) have to be computed to obtain a good estimate. Based on this observation, we present RapidPT, an algorithm that efficiently recovers the max null distribution commonly obtained through regular permutation testing in voxel-wise analysis. We present an extensive validation on a synthetic dataset and four varying sized datasets against two baselines: Statistical NonParametric Mapping (SnPM13) and a standard permutation testing implementation (referred as NaivePT). We find that RapidPT achieves its best runtime performance on medium sized datasets ($50 \leq n \leq 200$), with speedups of 1.5x - 38x (vs. SnPM13) and 20x-1000x (vs. NaivePT). For larger datasets ($n \geq 200$) RapidPT outperforms NaivePT (6x - 200x) on all datasets, and provides large speedups over SnPM13 when more than 10000 permutations (2x - 15x) are needed. The implementation is a standalone toolbox and also integrated within SnPM13, able to leverage multi-core architectures when available.