Accelerating Permutation Testing in Voxel-wise Analysis through Subspace Tracking: A new plugin for SnPM

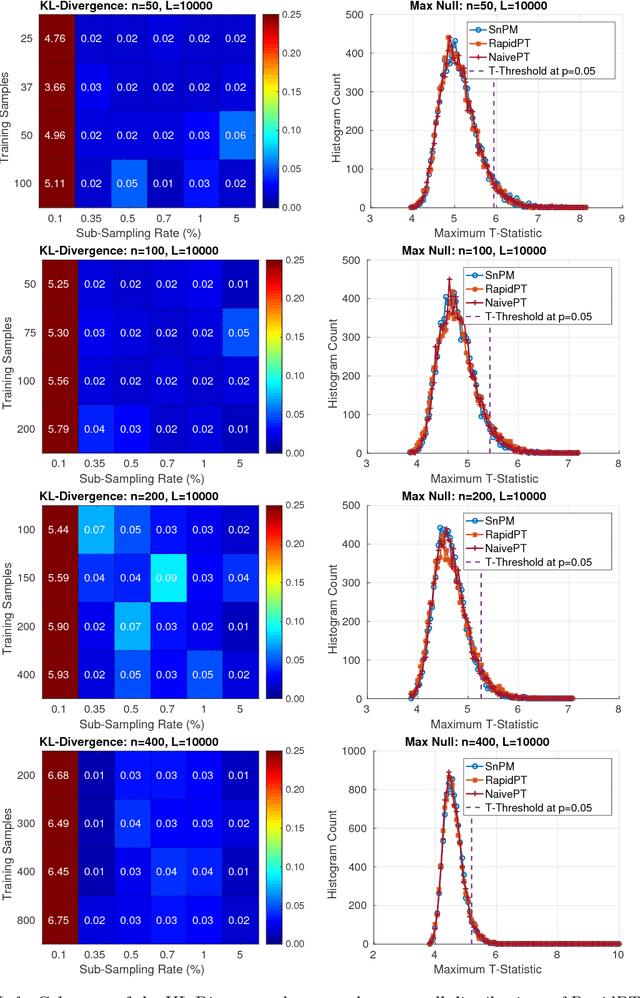
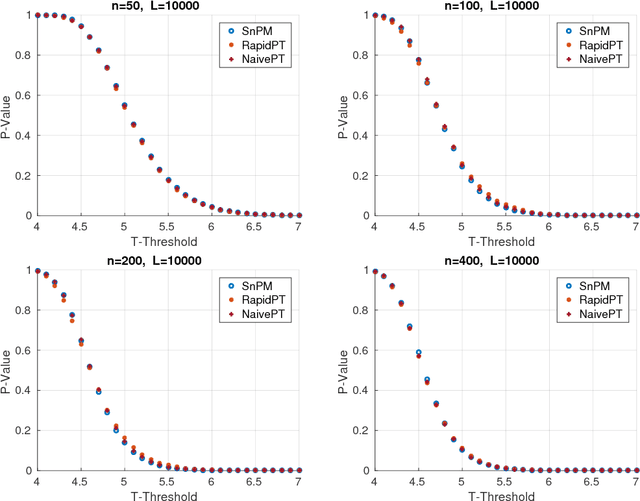
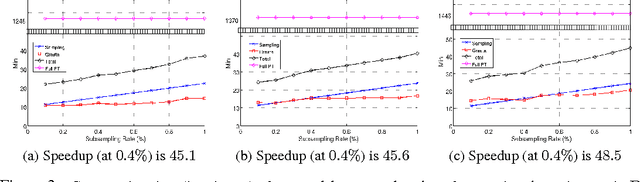
Permutation testing is a non-parametric method for obtaining the max null distribution used to compute corrected $p$-values that provide strong control of false positives. In neuroimaging, however, the computational burden of running such an algorithm can be significant. We find that by viewing the permutation testing procedure as the construction of a very large permutation testing matrix, $T$, one can exploit structural properties derived from the data and the test statistics to reduce the runtime under certain conditions. In particular, we see that $T$ is low-rank plus a low-variance residual. This makes $T$ a good candidate for low-rank matrix completion, where only a very small number of entries of $T$ ($\sim0.35\%$ of all entries in our experiments) have to be computed to obtain a good estimate. Based on this observation, we present RapidPT, an algorithm that efficiently recovers the max null distribution commonly obtained through regular permutation testing in voxel-wise analysis. We present an extensive validation on a synthetic dataset and four varying sized datasets against two baselines: Statistical NonParametric Mapping (SnPM13) and a standard permutation testing implementation (referred as NaivePT). We find that RapidPT achieves its best runtime performance on medium sized datasets ($50 \leq n \leq 200$), with speedups of 1.5x - 38x (vs. SnPM13) and 20x-1000x (vs. NaivePT). For larger datasets ($n \geq 200$) RapidPT outperforms NaivePT (6x - 200x) on all datasets, and provides large speedups over SnPM13 when more than 10000 permutations (2x - 15x) are needed. The implementation is a standalone toolbox and also integrated within SnPM13, able to leverage multi-core architectures when available.

Speeding up Permutation Testing in Neuroimaging

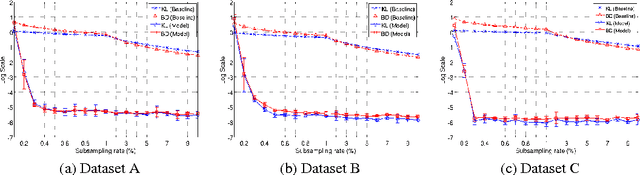
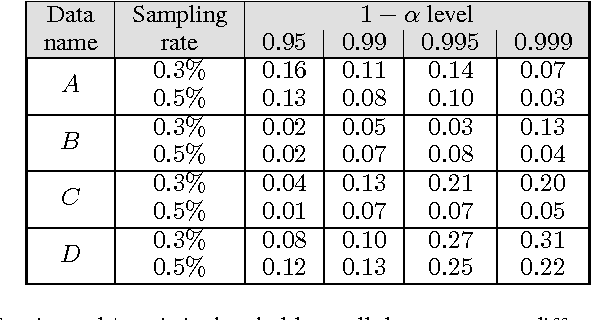
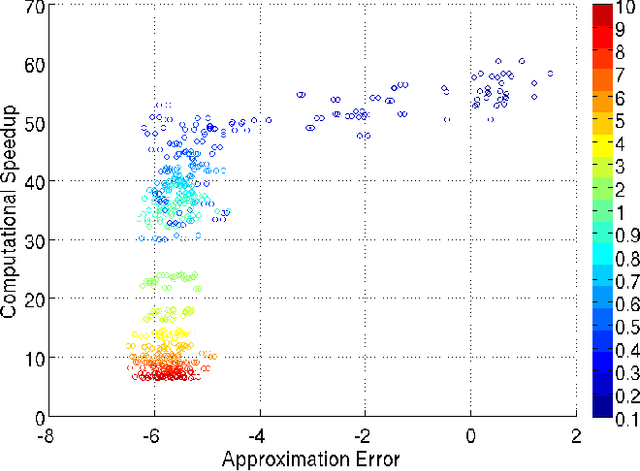
Multiple hypothesis testing is a significant problem in nearly all neuroimaging studies. In order to correct for this phenomena, we require a reliable estimate of the Family-Wise Error Rate (FWER). The well known Bonferroni correction method, while simple to implement, is quite conservative, and can substantially under-power a study because it ignores dependencies between test statistics. Permutation testing, on the other hand, is an exact, non-parametric method of estimating the FWER for a given $\alpha$-threshold, but for acceptably low thresholds the computational burden can be prohibitive. In this paper, we show that permutation testing in fact amounts to populating the columns of a very large matrix ${\bf P}$. By analyzing the spectrum of this matrix, under certain conditions, we see that ${\bf P}$ has a low-rank plus a low-variance residual decomposition which makes it suitable for highly sub--sampled --- on the order of $0.5\%$ --- matrix completion methods. Based on this observation, we propose a novel permutation testing methodology which offers a large speedup, without sacrificing the fidelity of the estimated FWER. Our evaluations on four different neuroimaging datasets show that a computational speedup factor of roughly $50\times$ can be achieved while recovering the FWER distribution up to very high accuracy. Further, we show that the estimated $\alpha$-threshold is also recovered faithfully, and is stable.