Simulating normalising constants with referenced thermodynamic integration: application to COVID-19 model selection

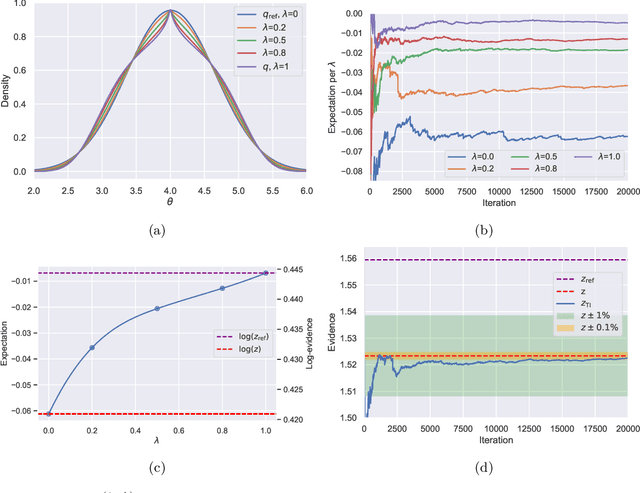
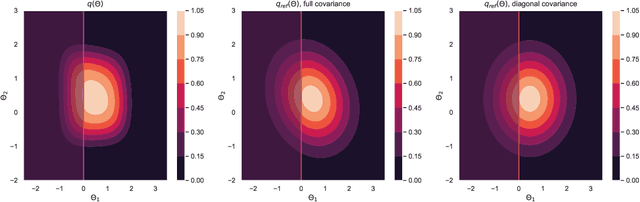
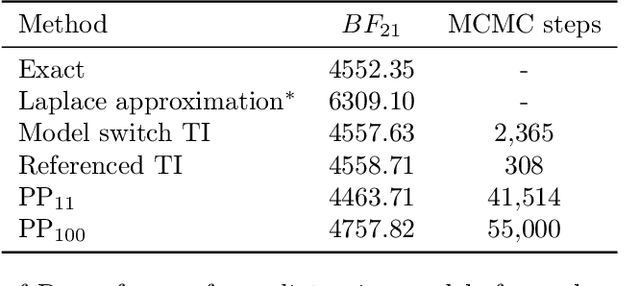
Model selection is a fundamental part of Bayesian statistical inference; a widely used tool in the field of epidemiology. Simple methods such as Akaike Information Criterion are commonly used but they do not incorporate the uncertainty of the model's parameters, which can give misleading choices when comparing models with similar fit to the data. One approach to model selection in a more rigorous way that uses the full posterior distributions of the models is to compute the ratio of the normalising constants (or model evidence), known as Bayes factors. These normalising constants integrate the posterior distribution over all parameters and balance over and under fitting. However, normalising constants often come in the form of intractable, high-dimensional integrals, therefore special probabilistic techniques need to be applied to correctly estimate the Bayes factors. One such method is thermodynamic integration (TI), which can be used to estimate the ratio of two models' evidence by integrating over a continuous path between the two un-normalised densities. In this paper we introduce a variation of the TI method, here referred to as referenced TI, which computes a single model's evidence in an efficient way by using a reference density such as a multivariate normal - where the normalising constant is known. We show that referenced TI, an asymptotically exact Monte Carlo method of calculating the normalising constant of a single model, in practice converges to the correct result much faster than other competing approaches such as the method of power posteriors. We illustrate the implementation of the algorithm on informative 1- and 2-dimensional examples, and apply it to a popular linear regression problem, and use it to select parameters for a model of the COVID-19 epidemic in South Korea.

A unified machine learning approach to time series forecasting applied to demand at emergency departments

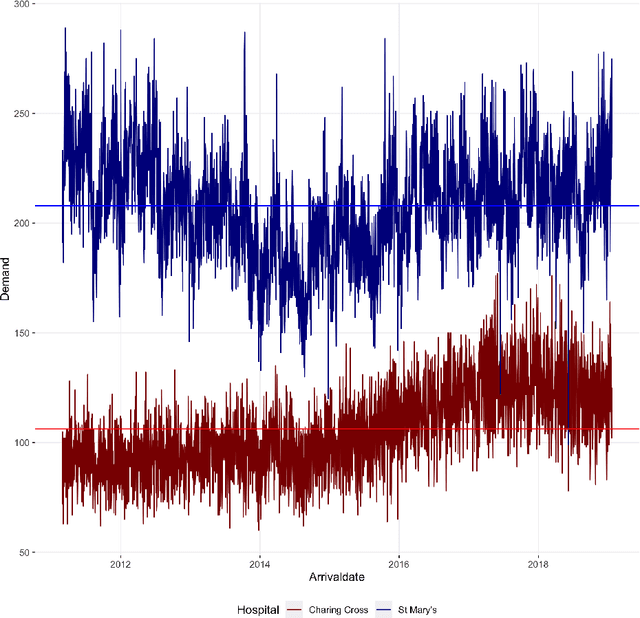
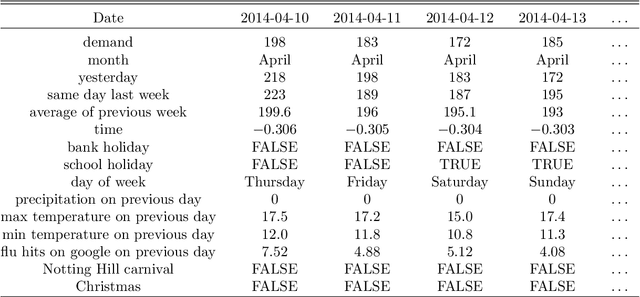
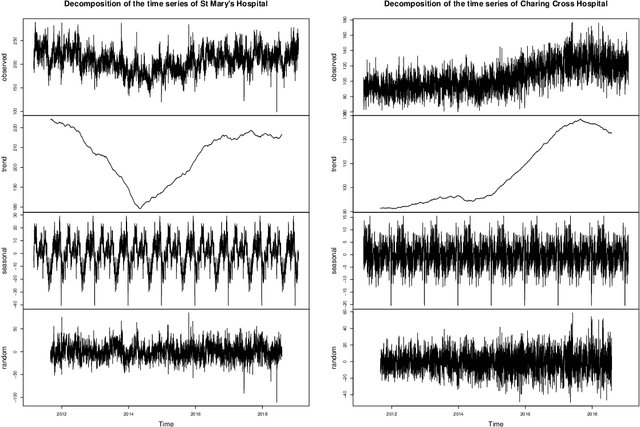
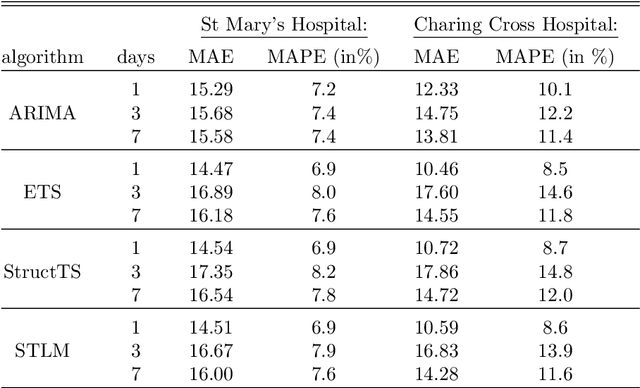
There were 25.6 million attendances at Emergency Departments (EDs) in England in 2019 corresponding to an increase of 12 million attendances over the past ten years. The steadily rising demand at EDs creates a constant challenge to provide adequate quality of care while maintaining standards and productivity. Managing hospital demand effectively requires an adequate knowledge of the future rate of admission. Using 8 years of electronic admissions data from two major acute care hospitals in London, we develop a novel ensemble methodology that combines the outcomes of the best performing time series and machine learning approaches in order to make highly accurate forecasts of demand, 1, 3 and 7 days in the future. Both hospitals face an average daily demand of 208 and 106 attendances respectively and experience considerable volatility around this mean. However, our approach is able to predict attendances at these emergency departments one day in advance up to a mean absolute error of +/- 14 and +/- 10 patients corresponding to a mean absolute percentage error of 6.8% and 8.6% respectively. Our analysis compares machine learning algorithms to more traditional linear models. We find that linear models often outperform machine learning methods and that the quality of our predictions for any of the forecasting horizons of 1, 3 or 7 days are comparable as measured in MAE. In addition to comparing and combining state-of-the-art forecasting methods to predict hospital demand, we consider two different hyperparameter tuning methods, enabling a faster deployment of our models without compromising performance. We believe our framework can readily be used to forecast a wide range of policy relevant indicators.