Gaussian Process Nowcasting: Application to COVID-19 Mortality Reporting

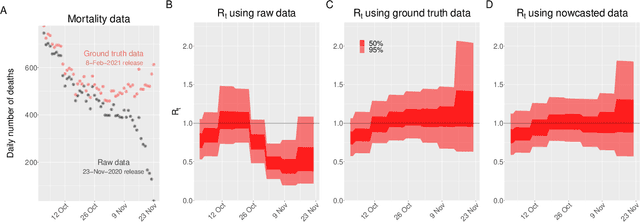
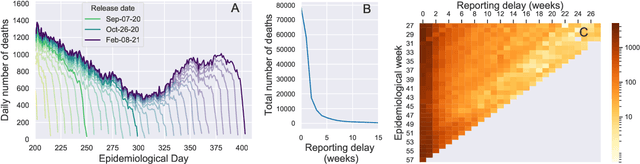
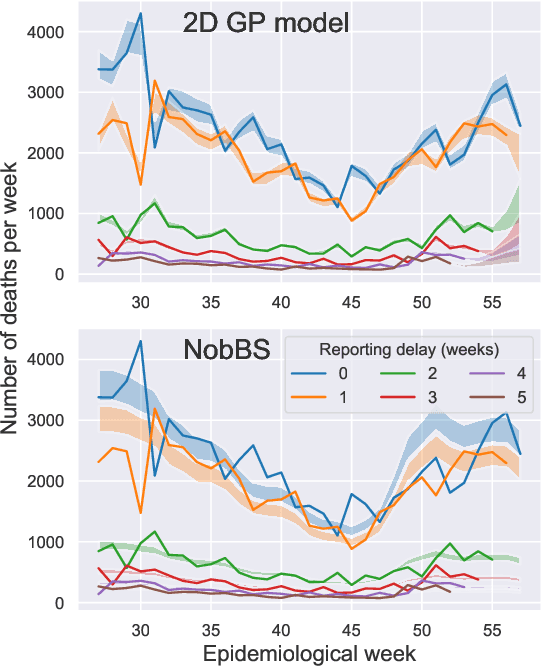
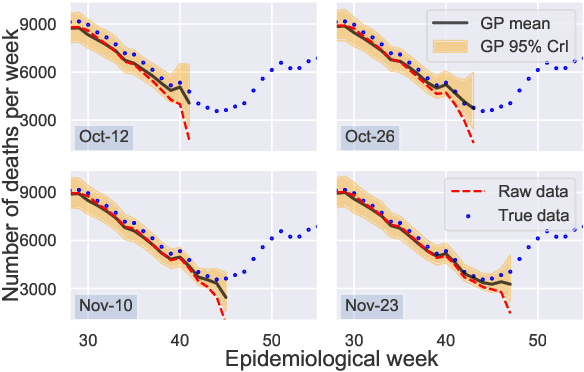
Updating observations of a signal due to the delays in the measurement process is a common problem in signal processing, with prominent examples in a wide range of fields. An important example of this problem is the nowcasting of COVID-19 mortality: given a stream of reported counts of daily deaths, can we correct for the delays in reporting to paint an accurate picture of the present, with uncertainty? Without this correction, raw data will often mislead by suggesting an improving situation. We present a flexible approach using a latent Gaussian process that is capable of describing the changing auto-correlation structure present in the reporting time-delay surface. This approach also yields robust estimates of uncertainty for the estimated nowcasted numbers of deaths. We test assumptions in model specification such as the choice of kernel or hyper priors, and evaluate model performance on a challenging real dataset from Brazil. Our experiments show that Gaussian process nowcasting performs favourably against both comparable methods, and a small sample of expert human predictions. Our approach has substantial practical utility in disease modelling -- by applying our approach to COVID-19 mortality data from Brazil, where reporting delays are large, we can make informative predictions on important epidemiological quantities such as the current effective reproduction number.

Simulating normalising constants with referenced thermodynamic integration: application to COVID-19 model selection

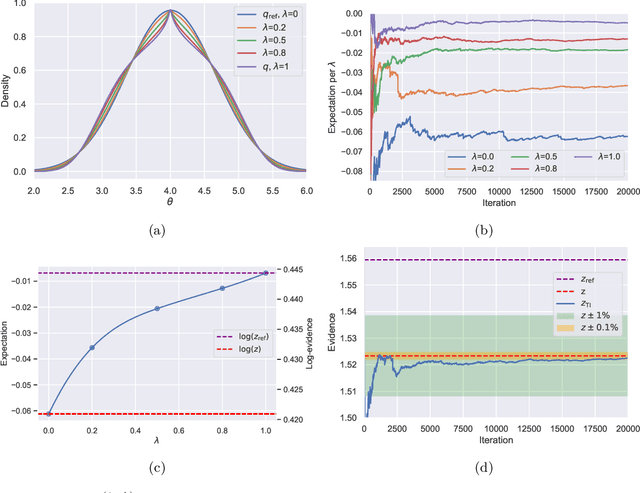
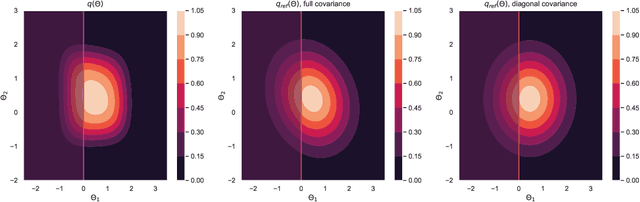
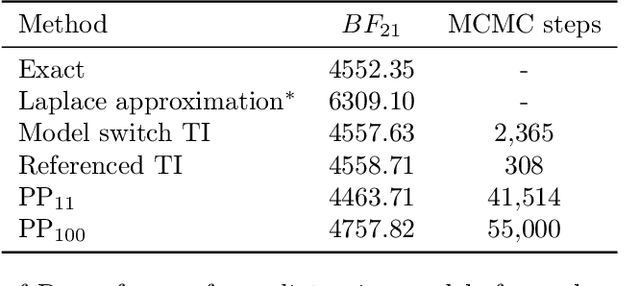
Model selection is a fundamental part of Bayesian statistical inference; a widely used tool in the field of epidemiology. Simple methods such as Akaike Information Criterion are commonly used but they do not incorporate the uncertainty of the model's parameters, which can give misleading choices when comparing models with similar fit to the data. One approach to model selection in a more rigorous way that uses the full posterior distributions of the models is to compute the ratio of the normalising constants (or model evidence), known as Bayes factors. These normalising constants integrate the posterior distribution over all parameters and balance over and under fitting. However, normalising constants often come in the form of intractable, high-dimensional integrals, therefore special probabilistic techniques need to be applied to correctly estimate the Bayes factors. One such method is thermodynamic integration (TI), which can be used to estimate the ratio of two models' evidence by integrating over a continuous path between the two un-normalised densities. In this paper we introduce a variation of the TI method, here referred to as referenced TI, which computes a single model's evidence in an efficient way by using a reference density such as a multivariate normal - where the normalising constant is known. We show that referenced TI, an asymptotically exact Monte Carlo method of calculating the normalising constant of a single model, in practice converges to the correct result much faster than other competing approaches such as the method of power posteriors. We illustrate the implementation of the algorithm on informative 1- and 2-dimensional examples, and apply it to a popular linear regression problem, and use it to select parameters for a model of the COVID-19 epidemic in South Korea.