Simulating normalising constants with referenced thermodynamic integration: application to COVID-19 model selection

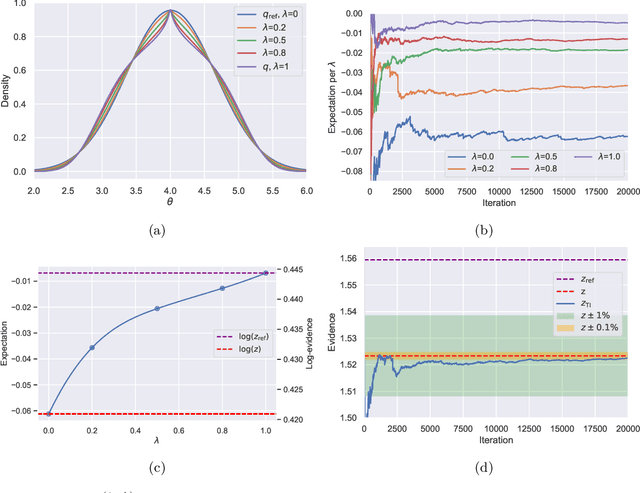
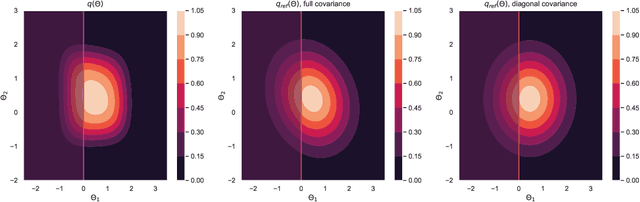
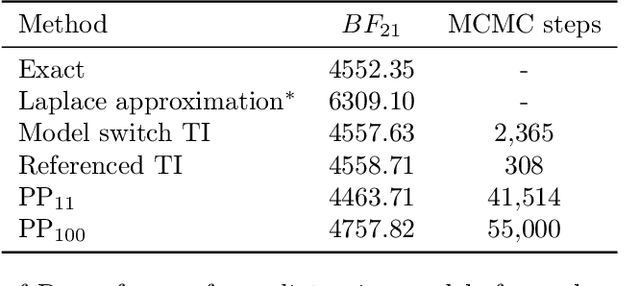
Model selection is a fundamental part of Bayesian statistical inference; a widely used tool in the field of epidemiology. Simple methods such as Akaike Information Criterion are commonly used but they do not incorporate the uncertainty of the model's parameters, which can give misleading choices when comparing models with similar fit to the data. One approach to model selection in a more rigorous way that uses the full posterior distributions of the models is to compute the ratio of the normalising constants (or model evidence), known as Bayes factors. These normalising constants integrate the posterior distribution over all parameters and balance over and under fitting. However, normalising constants often come in the form of intractable, high-dimensional integrals, therefore special probabilistic techniques need to be applied to correctly estimate the Bayes factors. One such method is thermodynamic integration (TI), which can be used to estimate the ratio of two models' evidence by integrating over a continuous path between the two un-normalised densities. In this paper we introduce a variation of the TI method, here referred to as referenced TI, which computes a single model's evidence in an efficient way by using a reference density such as a multivariate normal - where the normalising constant is known. We show that referenced TI, an asymptotically exact Monte Carlo method of calculating the normalising constant of a single model, in practice converges to the correct result much faster than other competing approaches such as the method of power posteriors. We illustrate the implementation of the algorithm on informative 1- and 2-dimensional examples, and apply it to a popular linear regression problem, and use it to select parameters for a model of the COVID-19 epidemic in South Korea.