Blind Ultrasound Image Enhancement via Self-Supervised Physics-Guided Degradation Modeling

Ultrasound (US) interpretation is hampered by multiplicative speckle, acquisition blur from the point-spread function (PSF), and scanner- and operator-dependent artifacts. Supervised enhancement methods assume access to clean targets or known degradations; conditions rarely met in practice. We present a blind, self-supervised enhancement framework that jointly deconvolves and denoises B-mode images using a Swin Convolutional U-Net trained with a \emph{physics-guided} degradation model. From each training frame, we extract rotated/cropped patches and synthesize inputs by (i) convolving with a Gaussian PSF surrogate and (ii) injecting noise via either spatial additive Gaussian noise or complex Fourier-domain perturbations that emulate phase/magnitude distortions. For US scans, clean-like targets are obtained via non-local low-rank (NLLR) denoising, removing the need for ground truth; for natural images, the originals serve as targets. Trained and validated on UDIAT~B, JNU-IFM, and XPIE Set-P, and evaluated additionally on a 700-image PSFHS test set, the method achieves the highest PSNR/SSIM across Gaussian and speckle noise levels, with margins that widen under stronger corruption. Relative to MSANN, Restormer, and DnCNN, it typically preserves an extra $\sim$1--4\,dB PSNR and 0.05--0.15 SSIM in heavy Gaussian noise, and $\sim$2--5\,dB PSNR and 0.05--0.20 SSIM under severe speckle. Controlled PSF studies show reduced FWHM and higher peak gradients, evidence of resolution recovery without edge erosion. Used as a plug-and-play preprocessor, it consistently boosts Dice for fetal head and pubic symphysis segmentation. Overall, the approach offers a practical, assumption-light path to robust US enhancement that generalizes across datasets, scanners, and degradation types.

Multi-Kernel Fusion for RBF Neural Networks

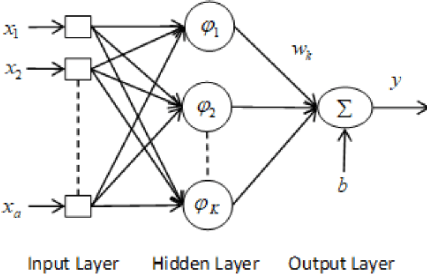
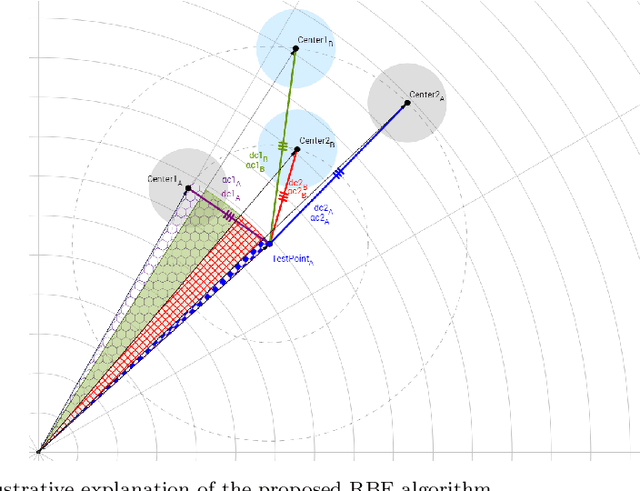
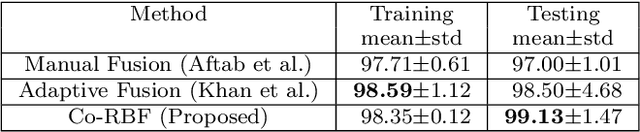
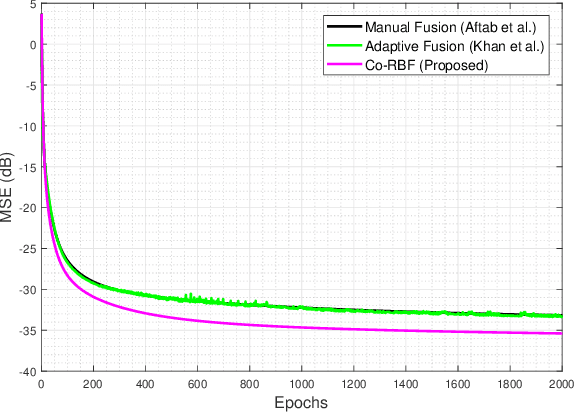
A simple yet effective architectural design of radial basis function neural networks (RBFNN) makes them amongst the most popular conventional neural networks. The current generation of radial basis function neural network is equipped with multiple kernels which provide significant performance benefits compared to the previous generation using only a single kernel. In existing multi-kernel RBF algorithms, multi-kernel is formed by the convex combination of the base/primary kernels. In this paper, we propose a novel multi-kernel RBFNN in which every base kernel has its own (local) weight. This novel flexibility in the network provides better performance such as faster convergence rate, better local minima and resilience against stucking in poor local minima. These performance gains are achieved at a competitive computational complexity compared to the contemporary multi-kernel RBF algorithms. The proposed algorithm is thoroughly analysed for performance gain using mathematical and graphical illustrations and also evaluated on three different types of problems namely: (i) pattern classification, (ii) system identification and (iii) function approximation. Empirical results clearly show the superiority of the proposed algorithm compared to the existing state-of-the-art multi-kernel approaches.