Discovering Symbolic Laws Directly from Trajectories with Hamiltonian Graph Neural Networks

The time evolution of physical systems is described by differential equations, which depend on abstract quantities like energy and force. Traditionally, these quantities are derived as functionals based on observables such as positions and velocities. Discovering these governing symbolic laws is the key to comprehending the interactions in nature. Here, we present a Hamiltonian graph neural network (HGNN), a physics-enforced GNN that learns the dynamics of systems directly from their trajectory. We demonstrate the performance of HGNN on n-springs, n-pendulums, gravitational systems, and binary Lennard Jones systems; HGNN learns the dynamics in excellent agreement with the ground truth from small amounts of data. We also evaluate the ability of HGNN to generalize to larger system sizes, and to hybrid spring-pendulum system that is a combination of two original systems (spring and pendulum) on which the models are trained independently. Finally, employing symbolic regression on the learned HGNN, we infer the underlying equations relating the energy functionals, even for complex systems such as the binary Lennard-Jones liquid. Our framework facilitates the interpretable discovery of interaction laws directly from physical system trajectories. Furthermore, this approach can be extended to other systems with topology-dependent dynamics, such as cells, polydisperse gels, or deformable bodies.

Graph Neural Stochastic Differential Equations for Learning Brownian Dynamics

Neural networks (NNs) that exploit strong inductive biases based on physical laws and symmetries have shown remarkable success in learning the dynamics of physical systems directly from their trajectory. However, these works focus only on the systems that follow deterministic dynamics, for instance, Newtonian or Hamiltonian dynamics. Here, we propose a framework, namely Brownian graph neural networks (BROGNET), combining stochastic differential equations (SDEs) and GNNs to learn Brownian dynamics directly from the trajectory. We theoretically show that BROGNET conserves the linear momentum of the system, which in turn, provides superior performance on learning dynamics as revealed empirically. We demonstrate this approach on several systems, namely, linear spring, linear spring with binary particle types, and non-linear spring systems, all following Brownian dynamics at finite temperatures. We show that BROGNET significantly outperforms proposed baselines across all the benchmarked Brownian systems. In addition, we demonstrate zero-shot generalizability of BROGNET to simulate unseen system sizes that are two orders of magnitude larger and to different temperatures than those used during training. Altogether, our study contributes to advancing the understanding of the intricate dynamics of Brownian motion and demonstrates the effectiveness of graph neural networks in modeling such complex systems.

Unravelling the Performance of Physics-informed Graph Neural Networks for Dynamical Systems

Recently, graph neural networks have been gaining a lot of attention to simulate dynamical systems due to their inductive nature leading to zero-shot generalizability. Similarly, physics-informed inductive biases in deep-learning frameworks have been shown to give superior performance in learning the dynamics of physical systems. There is a growing volume of literature that attempts to combine these two approaches. Here, we evaluate the performance of thirteen different graph neural networks, namely, Hamiltonian and Lagrangian graph neural networks, graph neural ODE, and their variants with explicit constraints and different architectures. We briefly explain the theoretical formulation highlighting the similarities and differences in the inductive biases and graph architecture of these systems. We evaluate these models on spring, pendulum, gravitational, and 3D deformable solid systems to compare the performance in terms of rollout error, conserved quantities such as energy and momentum, and generalizability to unseen system sizes. Our study demonstrates that GNNs with additional inductive biases, such as explicit constraints and decoupling of kinetic and potential energies, exhibit significantly enhanced performance. Further, all the physics-informed GNNs exhibit zero-shot generalizability to system sizes an order of magnitude larger than the training system, thus providing a promising route to simulate large-scale realistic systems.

Predicting Oxide Glass Properties with Low Complexity Neural Network and Physical and Chemical Descriptors

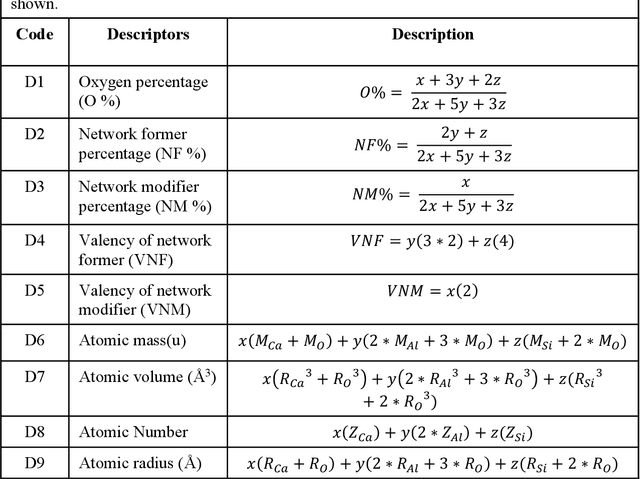
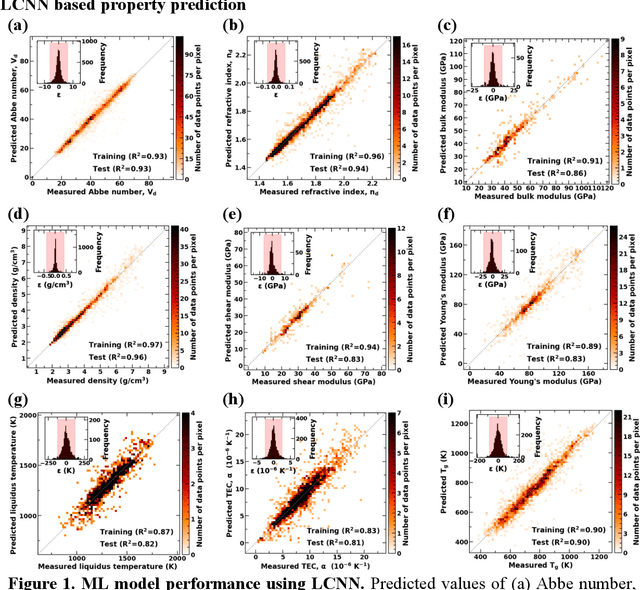
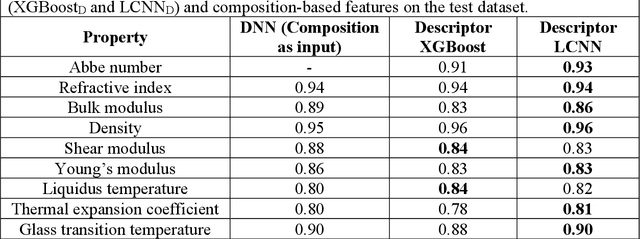
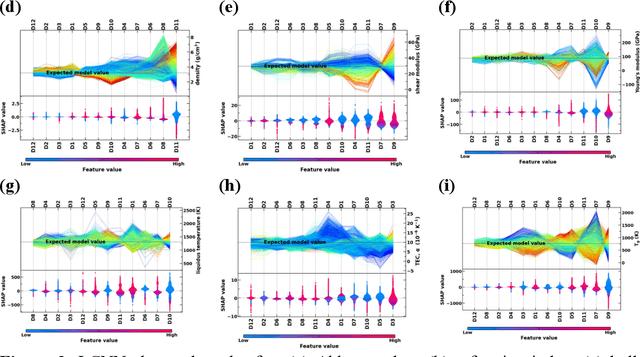
Due to their disordered structure, glasses present a unique challenge in predicting the composition-property relationships. Recently, several attempts have been made to predict the glass properties using machine learning techniques. However, these techniques have the limitations, namely, (i) predictions are limited to the components that are present in the original dataset, and (ii) predictions towards the extreme values of the properties, important regions for new materials discovery, are not very reliable due to the sparse datapoints in this region. To address these challenges, here we present a low complexity neural network (LCNN) that provides improved performance in predicting the properties of oxide glasses. In addition, we combine the LCNN with physical and chemical descriptors that allow the development of universal models that can provide predictions for components beyond the training set. By training on a large dataset (~50000) of glass components, we show the LCNN outperforms state-of-the-art algorithms such as XGBoost. In addition, we interpret the LCNN models using Shapely additive explanations to gain insights into the role played by the descriptors in governing the property. Finally, we demonstrate the universality of the LCNN models by predicting the properties for glasses with new components that were not present in the original training set. Altogether, the present approach provides a promising direction towards accelerated discovery of novel glass compositions.

Enhancing the Inductive Biases of Graph Neural ODE for Modeling Dynamical Systems

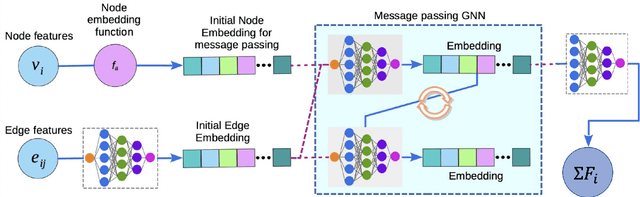
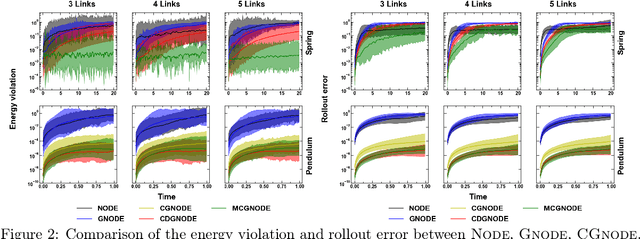
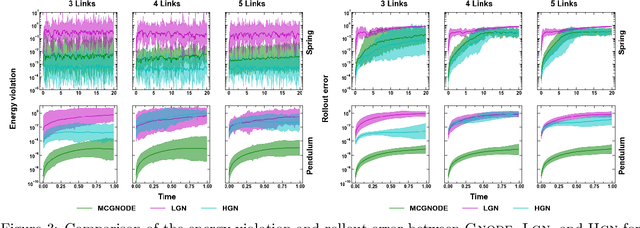
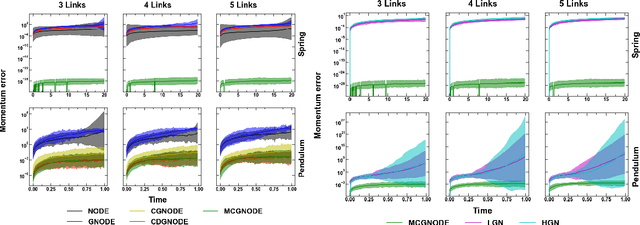
Neural networks with physics based inductive biases such as Lagrangian neural networks (LNN), and Hamiltonian neural networks (HNN) learn the dynamics of physical systems by encoding strong inductive biases. Alternatively, Neural ODEs with appropriate inductive biases have also been shown to give similar performances. However, these models, when applied to particle based systems, are transductive in nature and hence, do not generalize to large system sizes. In this paper, we present a graph based neural ODE, GNODE, to learn the time evolution of dynamical systems. Further, we carefully analyse the role of different inductive biases on the performance of GNODE. We show that, similar to LNN and HNN, encoding the constraints explicitly can significantly improve the training efficiency and performance of GNODE significantly. Our experiments also assess the value of additional inductive biases, such as Newtons third law, on the final performance of the model. We demonstrate that inducing these biases can enhance the performance of model by orders of magnitude in terms of both energy violation and rollout error. Interestingly, we observe that the GNODE trained with the most effective inductive biases, namely MCGNODE, outperforms the graph versions of LNN and HNN, namely, Lagrangian graph networks (LGN) and Hamiltonian graph networks (HGN) in terms of energy violation error by approx 4 orders of magnitude for a pendulum system, and approx 2 orders of magnitude for spring systems. These results suggest that competitive performances with energy conserving neural networks can be obtained for NODE based systems by inducing appropriate inductive biases.