Discovering Symbolic Laws Directly from Trajectories with Hamiltonian Graph Neural Networks

The time evolution of physical systems is described by differential equations, which depend on abstract quantities like energy and force. Traditionally, these quantities are derived as functionals based on observables such as positions and velocities. Discovering these governing symbolic laws is the key to comprehending the interactions in nature. Here, we present a Hamiltonian graph neural network (HGNN), a physics-enforced GNN that learns the dynamics of systems directly from their trajectory. We demonstrate the performance of HGNN on n-springs, n-pendulums, gravitational systems, and binary Lennard Jones systems; HGNN learns the dynamics in excellent agreement with the ground truth from small amounts of data. We also evaluate the ability of HGNN to generalize to larger system sizes, and to hybrid spring-pendulum system that is a combination of two original systems (spring and pendulum) on which the models are trained independently. Finally, employing symbolic regression on the learned HGNN, we infer the underlying equations relating the energy functionals, even for complex systems such as the binary Lennard-Jones liquid. Our framework facilitates the interpretable discovery of interaction laws directly from physical system trajectories. Furthermore, this approach can be extended to other systems with topology-dependent dynamics, such as cells, polydisperse gels, or deformable bodies.

Unravelling the Performance of Physics-informed Graph Neural Networks for Dynamical Systems

Recently, graph neural networks have been gaining a lot of attention to simulate dynamical systems due to their inductive nature leading to zero-shot generalizability. Similarly, physics-informed inductive biases in deep-learning frameworks have been shown to give superior performance in learning the dynamics of physical systems. There is a growing volume of literature that attempts to combine these two approaches. Here, we evaluate the performance of thirteen different graph neural networks, namely, Hamiltonian and Lagrangian graph neural networks, graph neural ODE, and their variants with explicit constraints and different architectures. We briefly explain the theoretical formulation highlighting the similarities and differences in the inductive biases and graph architecture of these systems. We evaluate these models on spring, pendulum, gravitational, and 3D deformable solid systems to compare the performance in terms of rollout error, conserved quantities such as energy and momentum, and generalizability to unseen system sizes. Our study demonstrates that GNNs with additional inductive biases, such as explicit constraints and decoupling of kinetic and potential energies, exhibit significantly enhanced performance. Further, all the physics-informed GNNs exhibit zero-shot generalizability to system sizes an order of magnitude larger than the training system, thus providing a promising route to simulate large-scale realistic systems.

Learning Rigid Body Dynamics with Lagrangian Graph Neural Network

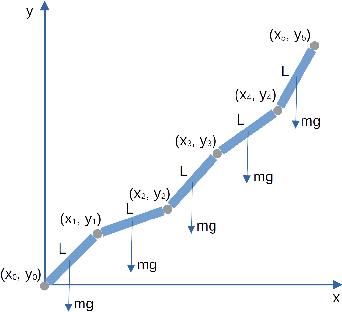
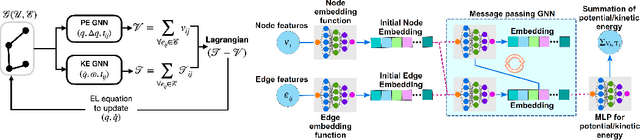
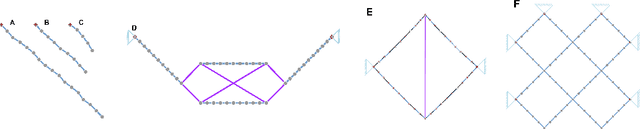
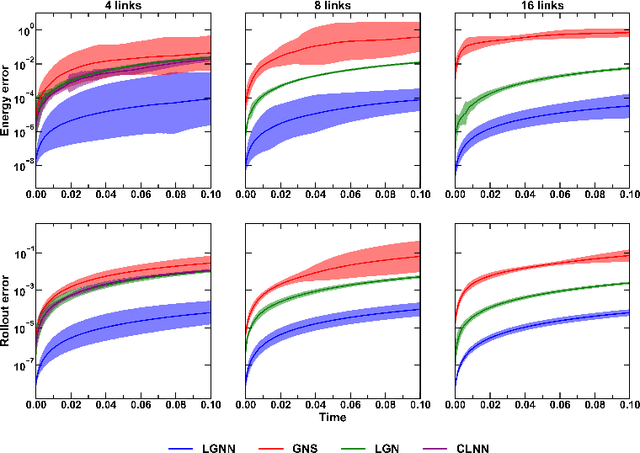
Lagrangian and Hamiltonian neural networks (LNN and HNN respectively) encode strong inductive biases that allow them to outperform other models of physical systems significantly. However, these models have, thus far, mostly been limited to simple systems such as pendulums and springs or a single rigid body such as a gyroscope or a rigid rotor. Here, we present a Lagrangian graph neural network (LGNN) that can learn the dynamics of rigid bodies by exploiting their topology. We demonstrate the performance of LGNN by learning the dynamics of ropes, chains, and trusses with the bars modeled as rigid bodies. LGNN also exhibits generalizability -- LGNN trained on chains with a few segments exhibits generalizability to simulate a chain with large number of links and arbitrary link length. We also show that the LGNN can simulate unseen hybrid systems including bars and chains, on which they have not been trained on. Specifically, we show that the LGNN can be used to model the dynamics of complex real-world structures such as the stability of tensegrity structures. Finally, we discuss the non-diagonal nature of the mass matrix and it's ability to generalize in complex systems.

Enhancing the Inductive Biases of Graph Neural ODE for Modeling Dynamical Systems

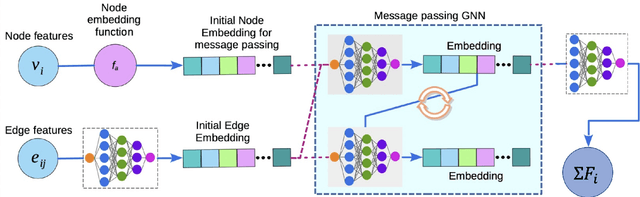
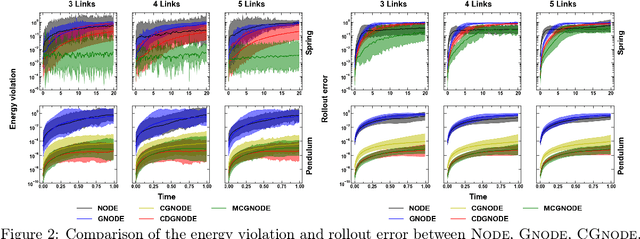
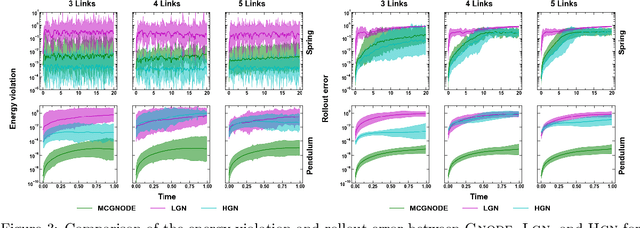
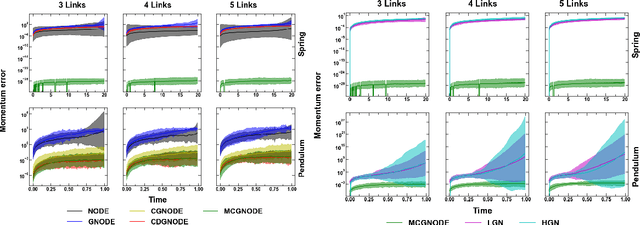
Neural networks with physics based inductive biases such as Lagrangian neural networks (LNN), and Hamiltonian neural networks (HNN) learn the dynamics of physical systems by encoding strong inductive biases. Alternatively, Neural ODEs with appropriate inductive biases have also been shown to give similar performances. However, these models, when applied to particle based systems, are transductive in nature and hence, do not generalize to large system sizes. In this paper, we present a graph based neural ODE, GNODE, to learn the time evolution of dynamical systems. Further, we carefully analyse the role of different inductive biases on the performance of GNODE. We show that, similar to LNN and HNN, encoding the constraints explicitly can significantly improve the training efficiency and performance of GNODE significantly. Our experiments also assess the value of additional inductive biases, such as Newtons third law, on the final performance of the model. We demonstrate that inducing these biases can enhance the performance of model by orders of magnitude in terms of both energy violation and rollout error. Interestingly, we observe that the GNODE trained with the most effective inductive biases, namely MCGNODE, outperforms the graph versions of LNN and HNN, namely, Lagrangian graph networks (LGN) and Hamiltonian graph networks (HGN) in terms of energy violation error by approx 4 orders of magnitude for a pendulum system, and approx 2 orders of magnitude for spring systems. These results suggest that competitive performances with energy conserving neural networks can be obtained for NODE based systems by inducing appropriate inductive biases.

Learning the Dynamics of Particle-based Systems with Lagrangian Graph Neural Networks

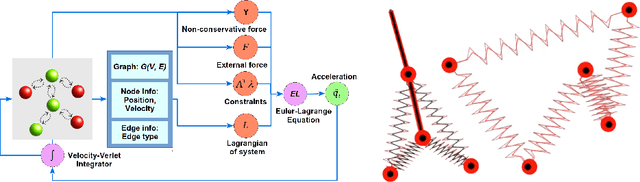
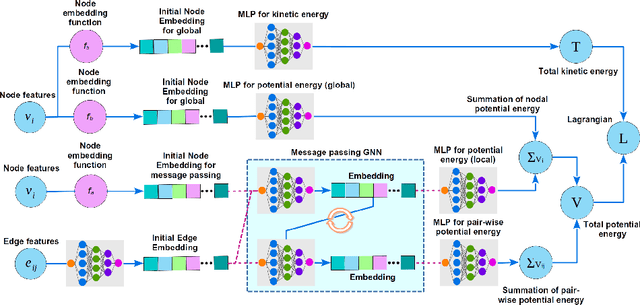
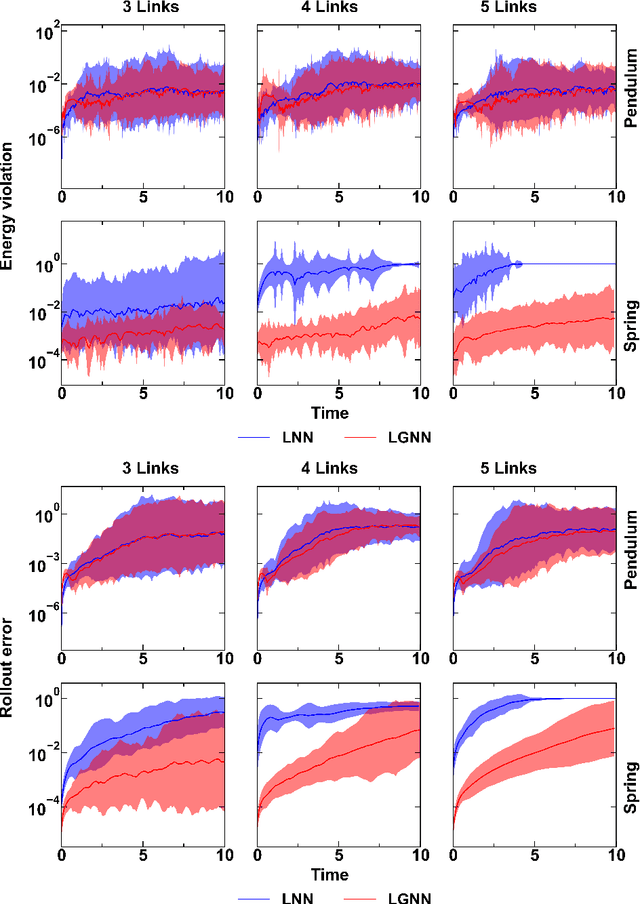
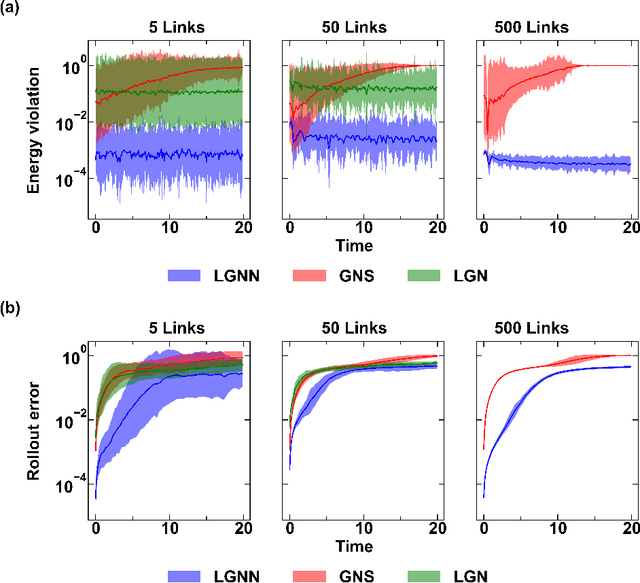
Physical systems are commonly represented as a combination of particles, the individual dynamics of which govern the system dynamics. However, traditional approaches require the knowledge of several abstract quantities such as the energy or force to infer the dynamics of these particles. Here, we present a framework, namely, Lagrangian graph neural network (LGnn), that provides a strong inductive bias to learn the Lagrangian of a particle-based system directly from the trajectory. We test our approach on challenging systems with constraints and drag -- LGnn outperforms baselines such as feed-forward Lagrangian neural network (Lnn) with improved performance. We also show the zero-shot generalizability of the system by simulating systems two orders of magnitude larger than the trained one and also hybrid systems that are unseen by the model, a unique feature. The graph architecture of LGnn significantly simplifies the learning in comparison to Lnn with ~25 times better performance on ~20 times smaller amounts of data. Finally, we show the interpretability of LGnn, which directly provides physical insights on drag and constraint forces learned by the model. LGnn can thus provide a fillip toward understanding the dynamics of physical systems purely from observable quantities.

Lagrangian Neural Network with Differentiable Symmetries and Relational Inductive Bias

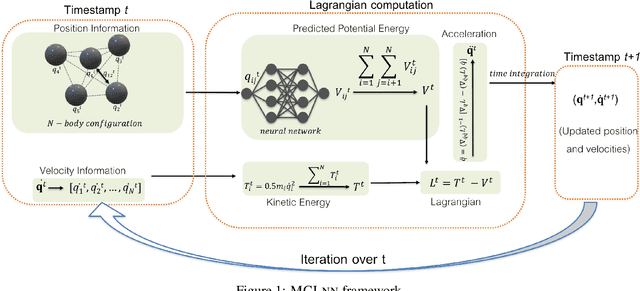
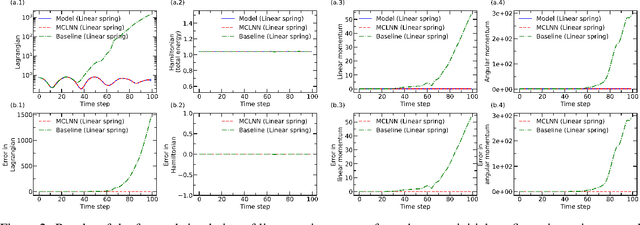
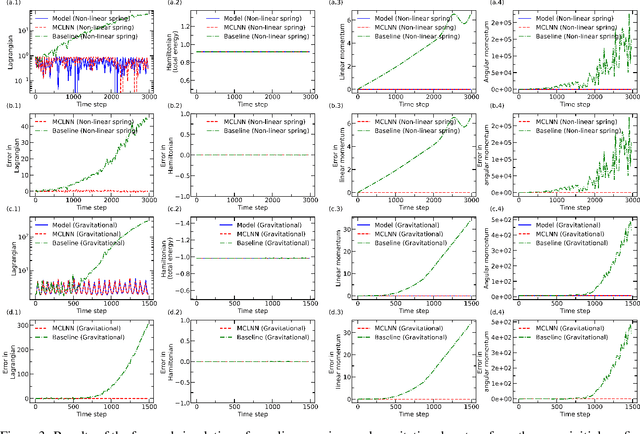
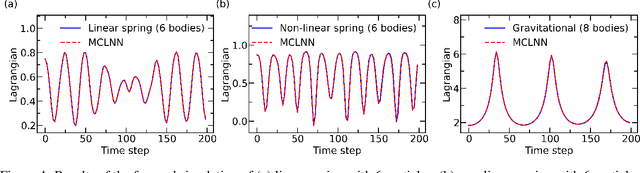
Realistic models of physical world rely on differentiable symmetries that, in turn, correspond to conservation laws. Recent works on Lagrangian and Hamiltonian neural networks show that the underlying symmetries of a system can be easily learned by a neural network when provided with an appropriate inductive bias. However, these models still suffer from issues such as inability to generalize to arbitrary system sizes, poor interpretability, and most importantly, inability to learn translational and rotational symmetries, which lead to the conservation laws of linear and angular momentum, respectively. Here, we present a momentum conserving Lagrangian neural network (MCLNN) that learns the Lagrangian of a system, while also preserving the translational and rotational symmetries. We test our approach on linear and non-linear spring systems, and a gravitational system, demonstrating the energy and momentum conservation. We also show that the model developed can generalize to systems of any arbitrary size. Finally, we discuss the interpretability of the MCLNN, which directly provides physical insights into the interactions of multi-particle systems.