S-SGD: Symmetrical Stochastic Gradient Descent with Weight Noise Injection for Reaching Flat Minima

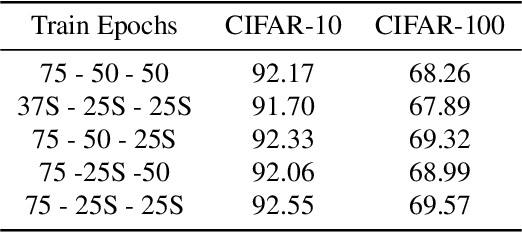
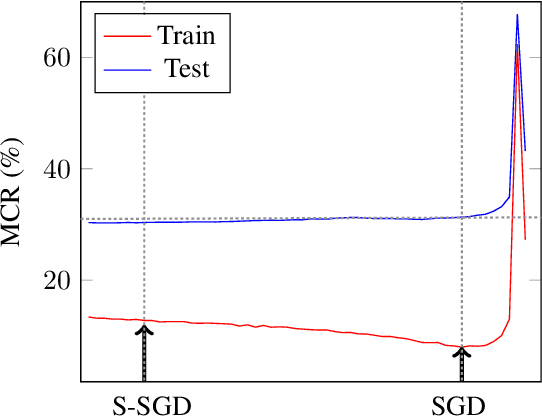
The stochastic gradient descent (SGD) method is most widely used for deep neural network (DNN) training. However, the method does not always converge to a flat minimum of the loss surface that can demonstrate high generalization capability. Weight noise injection has been extensively studied for finding flat minima using the SGD method. We devise a new weight-noise injection-based SGD method that adds symmetrical noises to the DNN weights. The training with symmetrical noise evaluates the loss surface at two adjacent points, by which convergence to sharp minima can be avoided. Fixed-magnitude symmetric noises are added to minimize training instability. The proposed method is compared with the conventional SGD method and previous weight-noise injection algorithms using convolutional neural networks for image classification. Particularly, performance improvements in large batch training are demonstrated. This method shows superior performance compared with conventional SGD and weight-noise injection methods regardless of the batch-size and learning rate scheduling algorithms.

Quantized Neural Networks: Characterization and Holistic Optimization

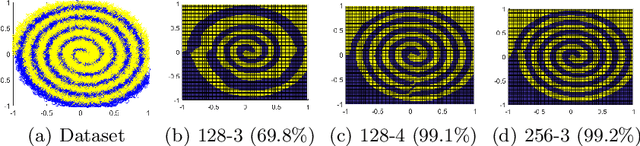
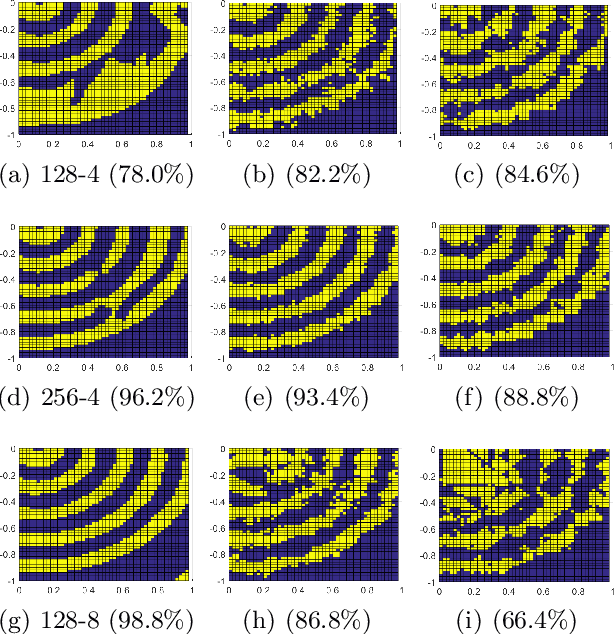
Quantized deep neural networks (QDNNs) are necessary for low-power, high throughput, and embedded applications. Previous studies mostly focused on developing optimization methods for the quantization of given models. However, quantization sensitivity depends on the model architecture. Therefore, the model selection needs to be a part of the QDNN design process. Also, the characteristics of weight and activation quantization are quite different. This study proposes a holistic approach for the optimization of QDNNs, which contains QDNN training methods as well as quantization-friendly architecture design. Synthesized data is used to visualize the effects of weight and activation quantization. The results indicate that deeper models are more prone to activation quantization, while wider models improve the resiliency to both weight and activation quantization. This study can provide insight into better optimization of QDNNs.

Overlapping Schwarz Decomposition for Nonlinear Optimal Control

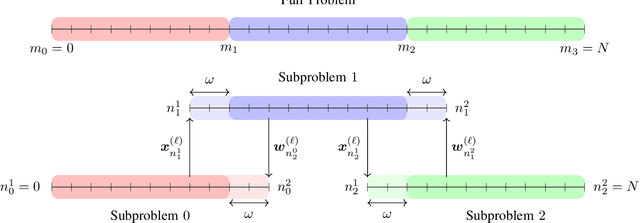
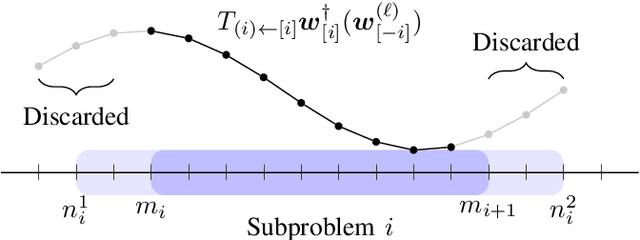
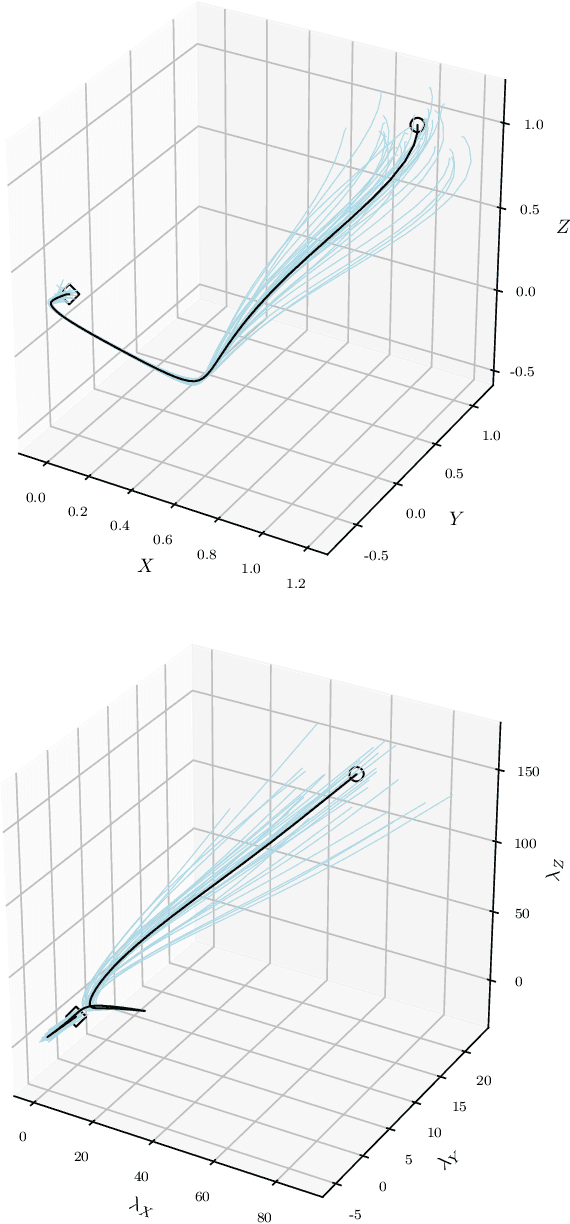
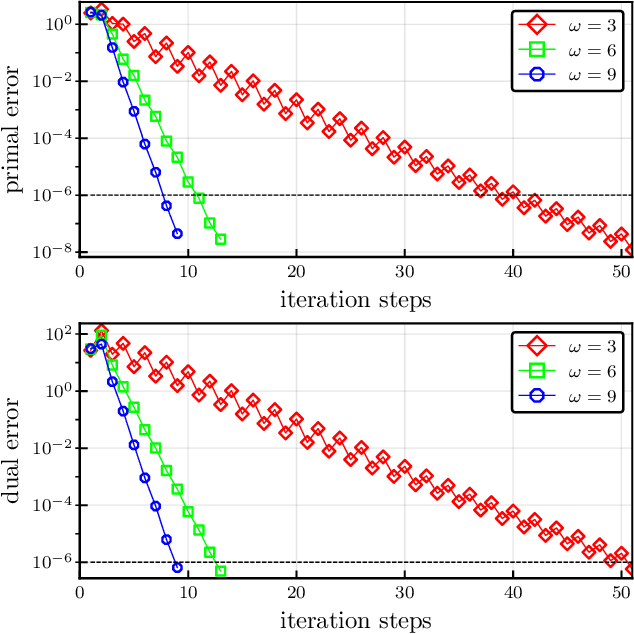
We present an overlapping Schwarz decomposition algorithm for solving nonlinear optimal control problems (OCPs). Our approach decomposes the time domain into a set of overlapping subdomains and solves subproblems defined over such subdomains in parallel. Convergence is attained by updating primal-dual information at the boundaries of the overlapping regions. We show that the algorithm exhibits local convergence and that the convergence rate improves exponentially with the size of the overlap. Our convergence results rely on a sensitivity result for OCPs that we call "asymptotic decay of sensitivity." Intuitively, this result states that impact of parametric perturbations at the boundaries of the time domain (initial and final time) decays exponentially as one moves away from the perturbation points. We show that this condition holds for nonlinear OCPs under a uniform second-order sufficient condition, a controllability condition, and a uniform boundedness condition. The approach is demonstrated by using a highly nonlinear quadrotor motion planning problem.

Unifying Theorems for Subspace Identification and Dynamic Mode Decomposition

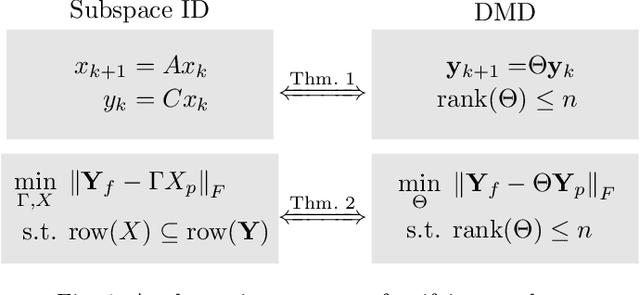
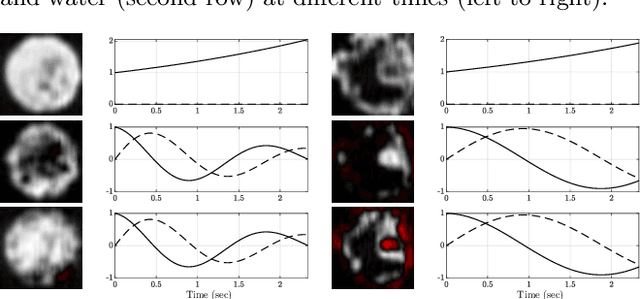
This paper presents unifying results for subspace identification (SID) and dynamic mode decomposition (DMD) for autonomous dynamical systems. We observe that SID seeks to solve an optimization problem to estimate an extended observability matrix and a state sequence that minimizes the prediction error for the state-space model. Moreover, we observe that DMD seeks to solve a rank-constrained matrix regression problem that minimizes the prediction error of an extended autoregressive model. We prove that existence conditions for perfect (error-free) state-space and low-rank extended autoregressive models are equivalent and that the SID and DMD optimization problems are equivalent. We exploit these results to propose a SID-DMD algorithm that delivers a provably optimal model and that is easy to implement. We demonstrate our developments using a case study that aims to build dynamical models directly from video data.

On the Convergence of the Dynamic Inner PCA Algorithm

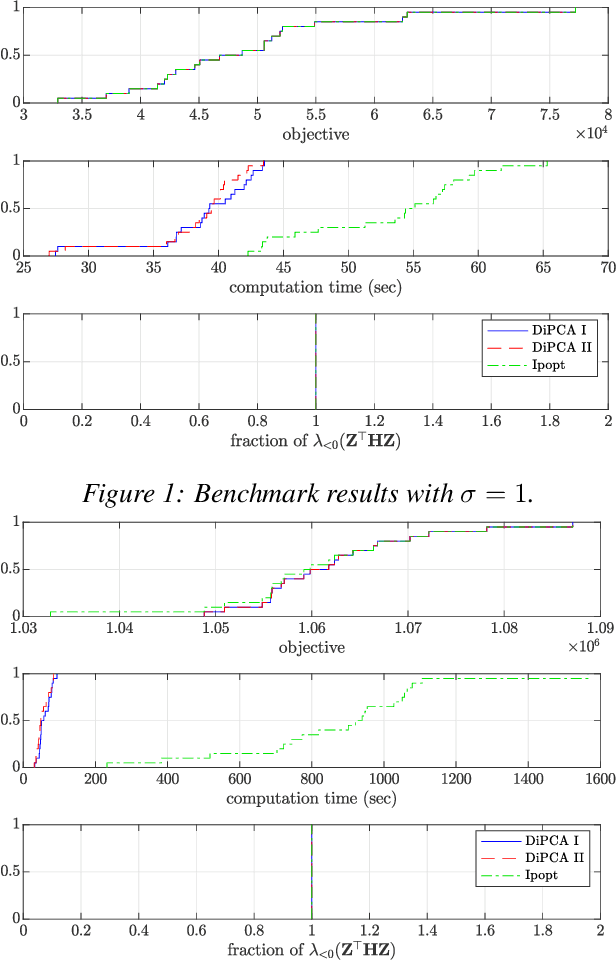
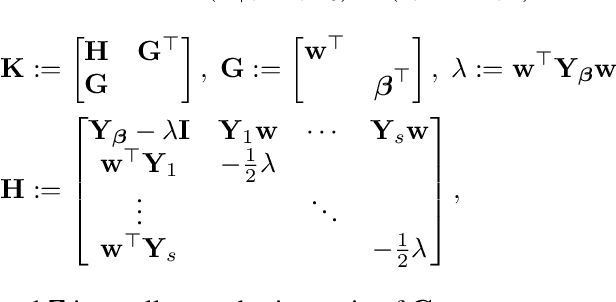
Dynamic inner principal component analysis (DiPCA) is a powerful method for the analysis of time-dependent multivariate data. DiPCA extracts dynamic latent variables that capture the most dominant temporal trends by solving a large-scale, dense, and nonconvex nonlinear program (NLP). A scalable decomposition algorithm has been recently proposed in the literature to solve these challenging NLPs. The decomposition algorithm performs well in practice but its convergence properties are not well understood. In this work, we show that this algorithm is a specialized variant of a coordinate maximization algorithm. This observation allows us to explain why the decomposition algorithm might work (or not) in practice and can guide improvements. We compare the performance of the decomposition strategies with that of the off-the-shelf solver Ipopt. The results show that decomposition is more scalable and, surprisingly, delivers higher quality solutions.

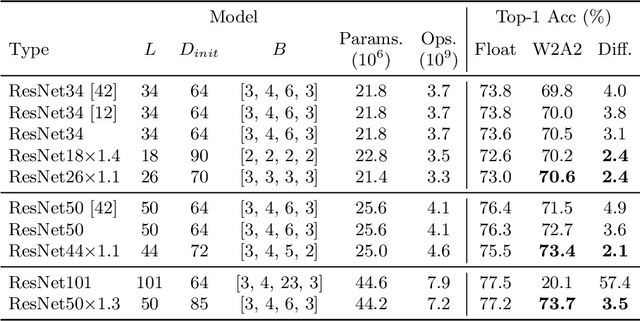
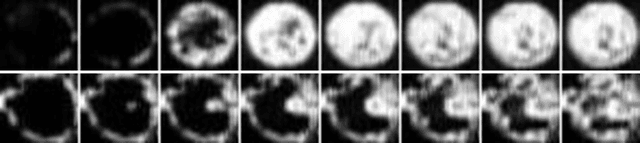
SQWA: Stochastic Quantized Weight Averaging for Improving the Generalization Capability of Low-Precision Deep Neural Networks

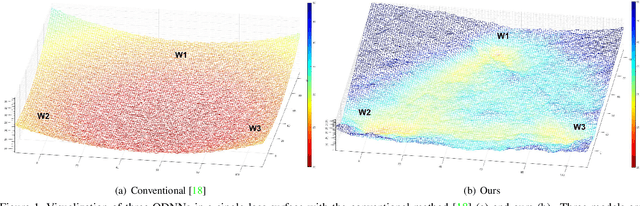
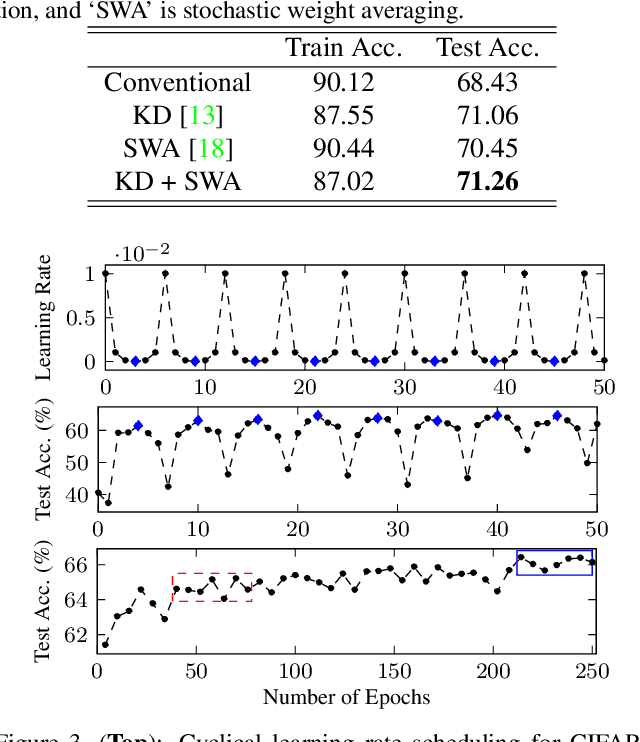
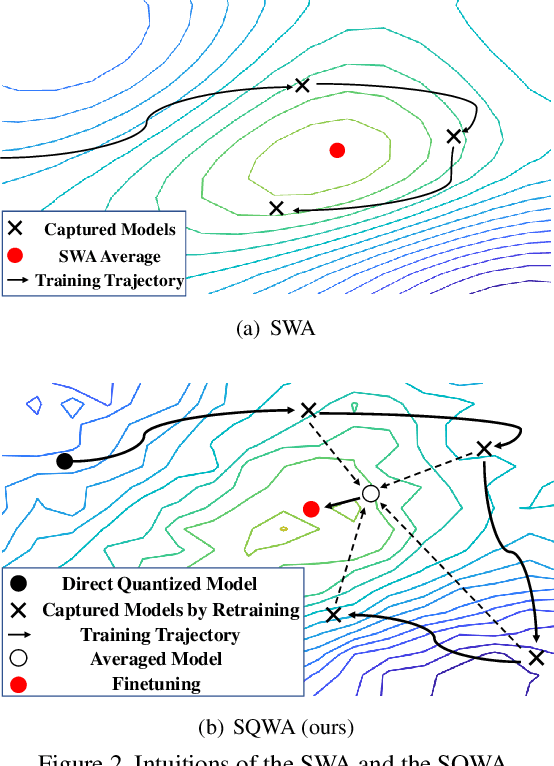
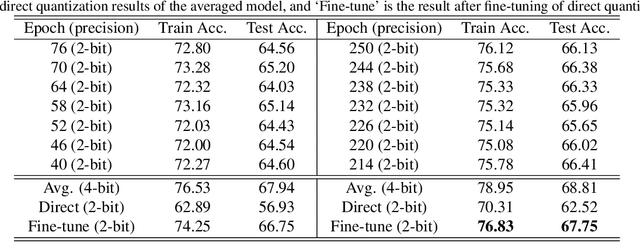
Designing a deep neural network (DNN) with good generalization capability is a complex process especially when the weights are severely quantized. Model averaging is a promising approach for achieving the good generalization capability of DNNs, especially when the loss surface for training contains many sharp minima. We present a new quantized neural network optimization approach, stochastic quantized weight averaging (SQWA), to design low-precision DNNs with good generalization capability using model averaging. The proposed approach includes (1) floating-point model training, (2) direct quantization of weights, (3) capturing multiple low-precision models during retraining with cyclical learning rates, (4) averaging the captured models, and (5) re-quantizing the averaged model and fine-tuning it with low-learning rates. Additionally, we present a loss-visualization technique on the quantized weight domain to clearly elucidate the behavior of the proposed method. Visualization results indicate that a quantized DNN (QDNN) optimized with the proposed approach is located near the center of the flat minimum in the loss surface. With SQWA training, we achieved state-of-the-art results for 2-bit QDNNs on CIFAR-100 and ImageNet datasets. Although we only employed a uniform quantization scheme for the sake of implementation in VLSI or low-precision neural processing units, the performance achieved exceeded those of previous studies employing non-uniform quantization.

Empirical Analysis of Knowledge Distillation Technique for Optimization of Quantized Deep Neural Networks

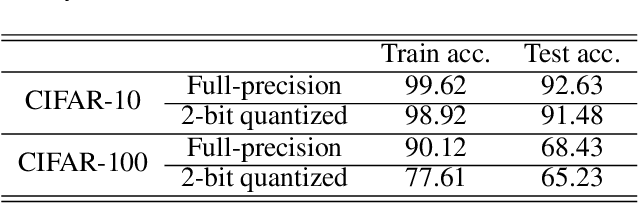
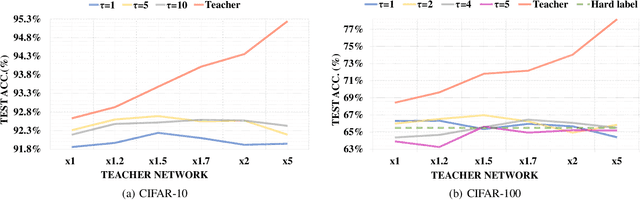
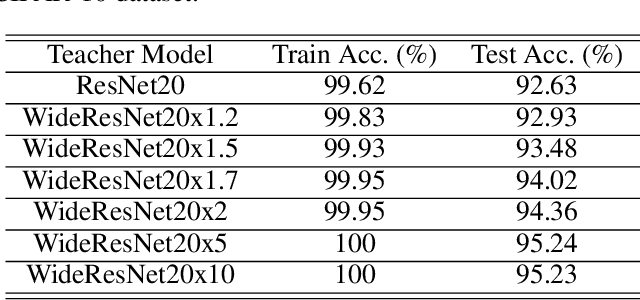
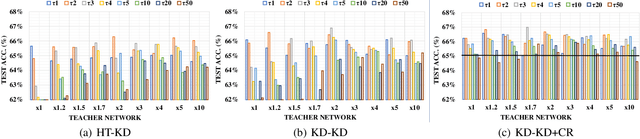
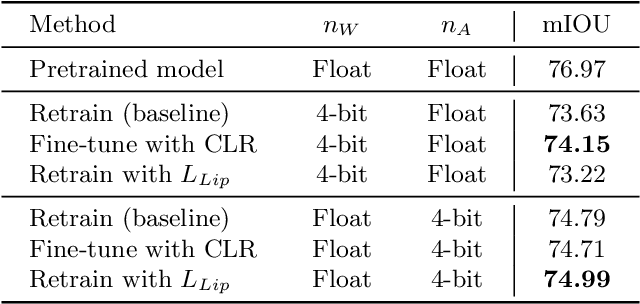
Knowledge distillation (KD) is a very popular method for model size reduction. Recently, the technique is exploited for quantized deep neural networks (QDNNs) training as a way to restore the performance sacrificed by word-length reduction. KD, however, employs additional hyper-parameters, such as temperature, coefficient, and the size of teacher network for QDNN training. We analyze the effect of these hyper-parameters for QDNN optimization with KD. We find that these hyper-parameters are inter-related, and also introduce a simple and effective technique that reduces \textit{coefficient} during training. With KD employing the proposed hyper-parameters, we achieve the test accuracy of 92.7% and 67.0% on Resnet20 with 2-bit ternary weights for CIFAR-10 and CIFAR-100 data sets, respectively.

Generative Knowledge Transfer for Neural Language Models

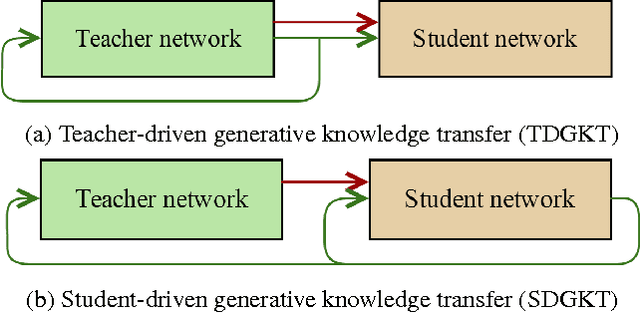
In this paper, we propose a generative knowledge transfer technique that trains an RNN based language model (student network) using text and output probabilities generated from a previously trained RNN (teacher network). The text generation can be conducted by either the teacher or the student network. We can also improve the performance by taking the ensemble of soft labels obtained from multiple teacher networks. This method can be used for privacy conscious language model adaptation because no user data is directly used for training. Especially, when the soft labels of multiple devices are aggregated via a trusted third party, we can expect very strong privacy protection.

Fixed-point optimization of deep neural networks with adaptive step size retraining

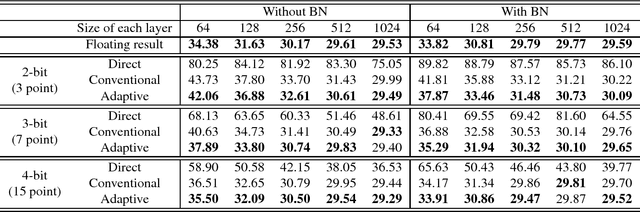
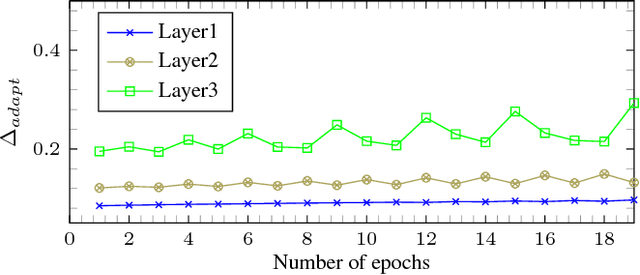
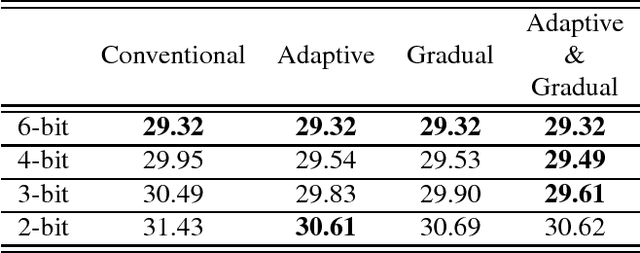
Fixed-point optimization of deep neural networks plays an important role in hardware based design and low-power implementations. Many deep neural networks show fairly good performance even with 2- or 3-bit precision when quantized weights are fine-tuned by retraining. We propose an improved fixedpoint optimization algorithm that estimates the quantization step size dynamically during the retraining. In addition, a gradual quantization scheme is also tested, which sequentially applies fixed-point optimizations from high- to low-precision. The experiments are conducted for feed-forward deep neural networks (FFDNNs), convolutional neural networks (CNNs), and recurrent neural networks (RNNs).

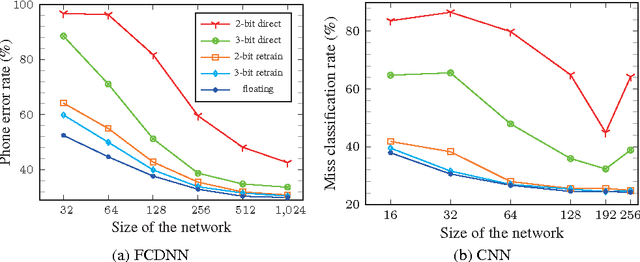
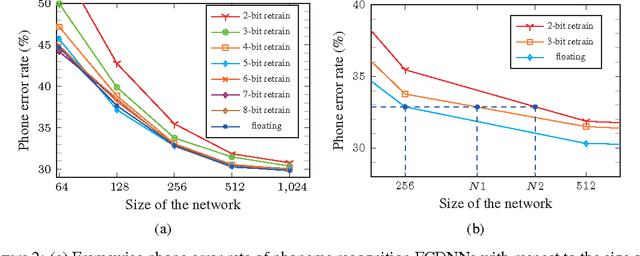
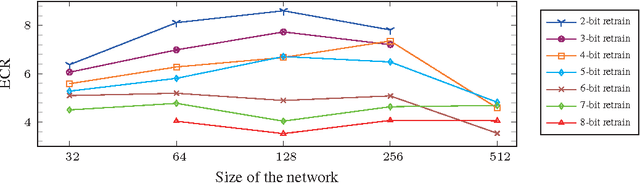
Quantized neural network design under weight capacity constraint

The complexity of deep neural network algorithms for hardware implementation can be lowered either by scaling the number of units or reducing the word-length of weights. Both approaches, however, can accompany the performance degradation although many types of research are conducted to relieve this problem. Thus, it is an important question which one, between the network size scaling and the weight quantization, is more effective for hardware optimization. For this study, the performances of fully-connected deep neural networks (FCDNNs) and convolutional neural networks (CNNs) are evaluated while changing the network complexity and the word-length of weights. Based on these experiments, we present the effective compression ratio (ECR) to guide the trade-off between the network size and the precision of weights when the hardware resource is limited.