Spencer Greenberg
Hypothesis Set Stability and Generalization
Apr 17, 2019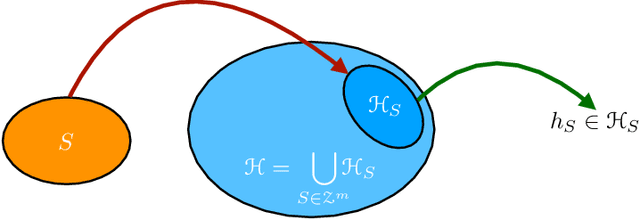
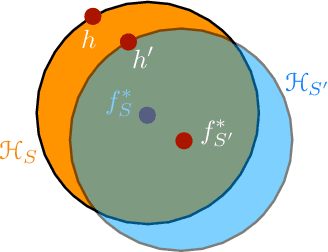
Abstract:We present an extensive study of generalization for data-dependent hypothesis sets. We give a general learning guarantee for data-dependent hypothesis sets based on a notion of transductive Rademacher complexity. Our main results are two generalization bounds for data-dependent hypothesis sets expressed in terms of a notion of hypothesis set stability and a notion of Rademacher complexity for data-dependent hypothesis sets that we introduce. These bounds admit as special cases both standard Rademacher complexity bounds and algorithm-dependent uniform stability bounds. We also illustrate the use of these learning bounds in the analysis of several scenarios.
Relative Deviation Learning Bounds and Generalization with Unbounded Loss Functions
Apr 04, 2016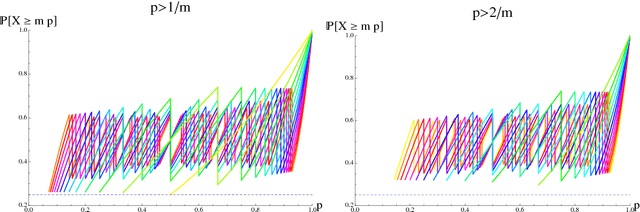
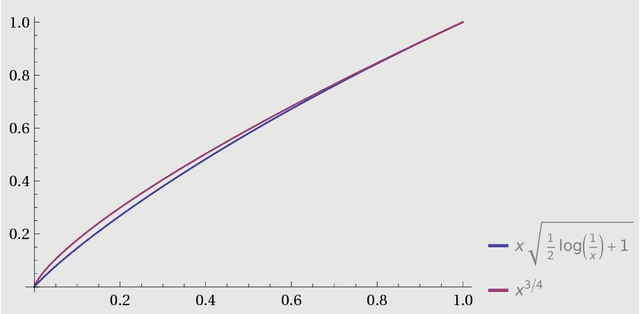
Abstract:We present an extensive analysis of relative deviation bounds, including detailed proofs of two-sided inequalities and their implications. We also give detailed proofs of two-sided generalization bounds that hold in the general case of unbounded loss functions, under the assumption that a moment of the loss is bounded. These bounds are useful in the analysis of importance weighting and other learning tasks such as unbounded regression.
Tight Lower Bound on the Probability of a Binomial Exceeding its Expectation
Nov 11, 2013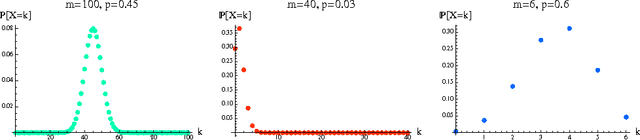
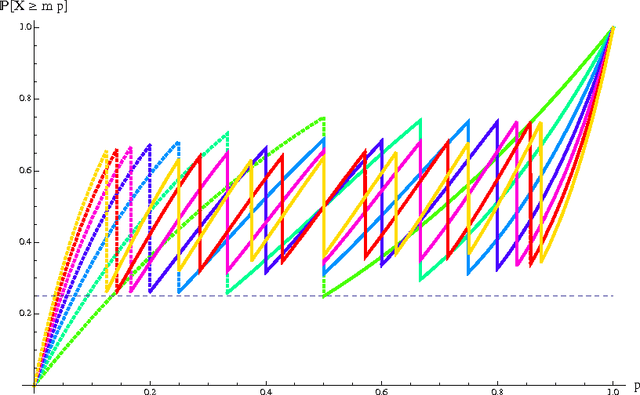
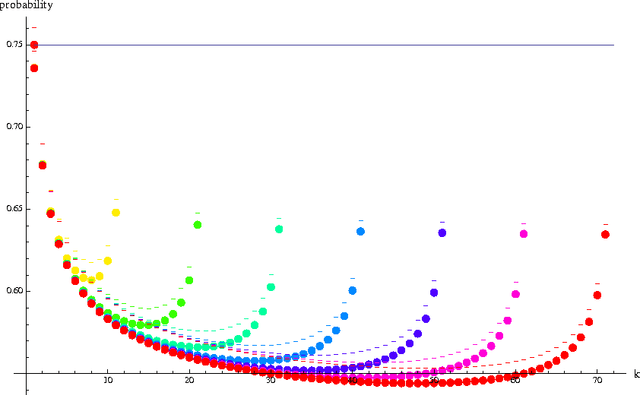
Abstract:We give the proof of a tight lower bound on the probability that a binomial random variable exceeds its expected value. The inequality plays an important role in a variety of contexts, including the analysis of relative deviation bounds in learning theory and generalization bounds for unbounded loss functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge