A Unified Framework for Locality in Scalable MARL

Scalable Multi-Agent Reinforcement Learning (MARL) is fundamentally challenged by the curse of dimensionality. A common solution is to exploit locality, which hinges on an Exponential Decay Property (EDP) of the value function. However, existing conditions that guarantee the EDP are often conservative, as they are based on worst-case, environment-only bounds (e.g., supremums over actions) and fail to capture the regularizing effect of the policy itself. In this work, we establish that locality can also be a \emph{policy-dependent} phenomenon. Our central contribution is a novel decomposition of the policy-induced interdependence matrix, $H^π$, which decouples the environment's sensitivity to state ($E^{\mathrm{s}}$) and action ($E^{\mathrm{a}}$) from the policy's sensitivity to state ($Π(π)$). This decomposition reveals that locality can be induced by a smooth policy (small $Π(π)$) even when the environment is strongly action-coupled, exposing a fundamental locality-optimality tradeoff. We use this framework to derive a general spectral condition $ρ(E^{\mathrm{s}}+E^{\mathrm{a}}Π(π)) < 1$ for exponential decay, which is strictly tighter than prior norm-based conditions. Finally, we leverage this theory to analyze a provably-sound localized block-coordinate policy improvement framework with guarantees tied directly to this spectral radius.

Flickering Multi-Armed Bandits

We introduce Flickering Multi-Armed Bandits (FMAB), a new MAB framework where the set of available arms (or actions) can change at each round, and the available set at any time may depend on the agent's previously selected arm. We model this constrained, evolving availability using random graph processes, where arms are nodes and the agent's movement is restricted to its local neighborhood. We analyze this problem under two random graph models: an i.i.d. Erdős--Rényi (ER) process and an Edge-Markovian process. We propose and analyze a two-phase algorithm that employs a lazy random walk for exploration to efficiently identify the optimal arm, followed by a navigation and commitment phase for exploitation. We establish high-probability and expected sublinear regret bounds for both graph settings. We show that the exploration cost of our algorithm is near-optimal by establishing a matching information-theoretic lower bound for this problem class, highlighting the fundamental cost of exploration under local-move constraints. We complement our theoretical guarantees with numerical simulations, including a scenario of a robotic ground vehicle scouting a disaster-affected region.

Multi-Agent Lipschitz Bandits

We study the decentralized multi-player stochastic bandit problem over a continuous, Lipschitz-structured action space where hard collisions yield zero reward. Our objective is to design a communication-free policy that maximizes collective reward, with coordination costs that are independent of the time horizon $T$. We propose a modular protocol that first solves the multi-agent coordination problem -- identifying and seating players on distinct high-value regions via a novel maxima-directed search -- and then decouples the problem into $N$ independent single-player Lipschitz bandits. We establish a near-optimal regret bound of $\tilde{O}(T^{(d+1)/(d+2)})$ plus a $T$-independent coordination cost, matching the single-player rate. To our knowledge, this is the first framework providing such guarantees, and it extends to general distance-threshold collision models.

Incentivized Lipschitz Bandits

We study incentivized exploration in multi-armed bandit (MAB) settings with infinitely many arms modeled as elements in continuous metric spaces. Unlike classical bandit models, we consider scenarios where the decision-maker (principal) incentivizes myopic agents to explore beyond their greedy choices through compensation, but with the complication of reward drift--biased feedback arising due to the incentives. We propose novel incentivized exploration algorithms that discretize the infinite arm space uniformly and demonstrate that these algorithms simultaneously achieve sublinear cumulative regret and sublinear total compensation. Specifically, we derive regret and compensation bounds of $\Tilde{O}(T^{d+1/d+2})$, with $d$ representing the covering dimension of the metric space. Furthermore, we generalize our results to contextual bandits, achieving comparable performance guarantees. We validate our theoretical findings through numerical simulations.

Characterizing and Optimizing LLM Inference Workloads on CPU-GPU Coupled Architectures

Large language model (LLM)-based inference workloads increasingly dominate data center costs and resource utilization. Therefore, understanding the inference workload characteristics on evolving CPU-GPU coupled architectures is crucial for optimization. This paper presents an in-depth analysis of LLM inference behavior on loosely-coupled (PCIe A100/H100) and closely-coupled (GH200) systems. We analyze performance dynamics using fine-grained operator-to-kernel trace analysis, facilitated by our novel profiler SKIP and metrics like Total Kernel Launch and Queuing Time (TKLQT). Results show that closely-coupled (CC) GH200 significantly outperforms loosely-coupled (LC) systems at large batch sizes, achieving 1.9x-2.7x faster prefill latency for Llama 3.2-1B. However, our analysis also reveals that GH200 remains CPU-bound up to 4x larger batch sizes than LC systems. In this extended CPU-bound region, we identify the performance characteristics of the Grace CPU as a key factor contributing to higher inference latency at low batch sizes on GH200. We demonstrate that TKLQT accurately identifies this CPU/GPU-bound transition point. Based on this analysis, we further show that kernel fusion offers significant potential to mitigate GH200's low-batch latency bottleneck by reducing kernel launch overhead. This detailed kernel-level characterization provides critical insights for optimizing diverse CPU-GPU coupling strategies. This work is an initial effort, and we plan to explore other major AI/DL workloads that demand different degrees of CPU-GPU heterogeneous architectures.

Testing Credibility of Public and Private Surveys through the Lens of Regression

Testing whether a sample survey is a credible representation of the population is an important question to ensure the validity of any downstream research. While this problem, in general, does not have an efficient solution, one might take a task-based approach and aim to understand whether a certain data analysis tool, like linear regression, would yield similar answers both on the population and the sample survey. In this paper, we design an algorithm to test the credibility of a sample survey in terms of linear regression. In other words, we design an algorithm that can certify if a sample survey is good enough to guarantee the correctness of data analysis done using linear regression tools. Nowadays, one is naturally concerned about data privacy in surveys. Thus, we further test the credibility of surveys published in a differentially private manner. Specifically, we focus on Local Differential Privacy (LDP), which is a standard technique to ensure privacy in surveys where the survey participants might not trust the aggregator. We extend our algorithm to work even when the data analysis has been done using surveys with LDP. In the process, we also propose an algorithm that learns with high probability the guarantees a linear regression model on a survey published with LDP. Our algorithm also serves as a mechanism to learn linear regression models from data corrupted with noise coming from any subexponential distribution. We prove that it achieves the optimal estimation error bound for $\ell_1$ linear regression, which might be of broader interest. We prove the theoretical correctness of our algorithms while trying to reduce the sample complexity for both public and private surveys. We also numerically demonstrate the performance of our algorithms on real and synthetic datasets.

Incentivized Exploration of Non-Stationary Stochastic Bandits

We study incentivized exploration for the multi-armed bandit (MAB) problem with non-stationary reward distributions, where players receive compensation for exploring arms other than the greedy choice and may provide biased feedback on the reward. We consider two different non-stationary environments: abruptly-changing and continuously-changing, and propose respective incentivized exploration algorithms. We show that the proposed algorithms achieve sublinear regret and compensation over time, thus effectively incentivizing exploration despite the nonstationarity and the biased or drifted feedback.

On simple expectations and observations of intelligent agents: A complexity study

Public observation logic (POL) reasons about agent expectations and agent observations in various real world situations. The expectations of agents take shape based on certain protocols about the world around and they remove those possible scenarios where their expectations and observations do not match. This in turn influences the epistemic reasoning of these agents. In this work, we study the computational complexity of the satisfaction problems of various fragments of POL. In the process, we also highlight the inevitable link that these fragments have with the well-studied Public announcement logic.

On verifying expectations and observations of intelligent agents

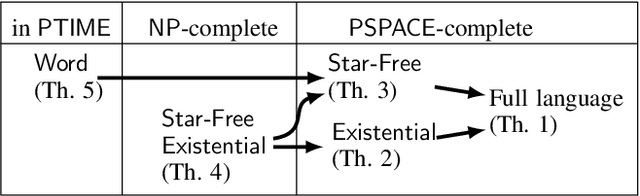
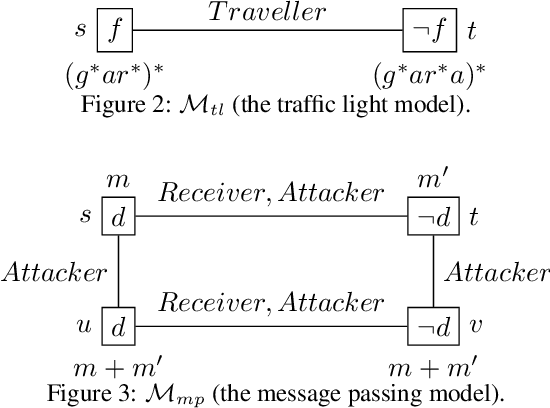
Public observation logic (POL) is a variant of dynamic epistemic logic to reason about agent expectations and agent observations. Agents have certain expectations, regarding the situation at hand, that are actuated by the relevant protocols, and they eliminate possible worlds in which their expectations do not match with their observations. In this work, we investigate the computational complexity of the model checking problem for POL and prove its PSPACE-completeness. We also study various syntactic fragments of POL. We exemplify the applicability of POL model checking in verifying different characteristics and features of an interactive system with respect to the distinct expectations and (matching) observations of the system. Finally, we provide a discussion on the implementation of the model checking algorithms.

Two new results about quantum exact learning

We present two new results about exact learning by quantum computers. First, we show how to exactly learn a $k$-Fourier-sparse $n$-bit Boolean function from $O(k^{1.5}(\log k)^2)$ uniform quantum examples for that function. This improves over the bound of $\widetilde{\Theta}(kn)$ uniformly random \emph{classical} examples (Haviv and Regev, CCC'15). Second, we show that if a concept class $\mathcal{C}$ can be exactly learned using $Q$ quantum membership queries, then it can also be learned using $O\left(\frac{Q^2}{\log Q}\log|\mathcal{C}|\right)$ \emph{classical} membership queries. This improves the previous-best simulation result (Servedio and Gortler, SICOMP'04) by a $\log Q$-factor.