Optimizing Data Distribution and Kernel Performance for Efficient Training of Chemistry Foundation Models: A Case Study with MACE

Chemistry Foundation Models (CFMs) that leverage Graph Neural Networks (GNNs) operating on 3D molecular graph structures are becoming indispensable tools for computational chemists and materials scientists. These models facilitate the understanding of matter and the discovery of new molecules and materials. In contrast to GNNs operating on a large homogeneous graphs, GNNs used by CFMs process a large number of geometric graphs of varying sizes, requiring different optimization strategies than those developed for large homogeneous GNNs. This paper presents optimizations for two critical phases of CFM training: data distribution and model training, targeting MACE - a state-of-the-art CFM. We address the challenge of load balancing in data distribution by formulating it as a multi-objective bin packing problem. We propose an iterative algorithm that provides a highly effective, fast, and practical solution, ensuring efficient data distribution. For the training phase, we identify symmetric tensor contraction as the key computational kernel in MACE and optimize this kernel to improve the overall performance. Our combined approach of balanced data distribution and kernel optimization significantly enhances the training process of MACE. Experimental results demonstrate a substantial speedup, reducing per-epoch execution time for training from 12 to 2 minutes on 740 GPUs with a 2.6M sample dataset.

HydroNet: Benchmark Tasks for Preserving Intermolecular Interactions and Structural Motifs in Predictive and Generative Models for Molecular Data

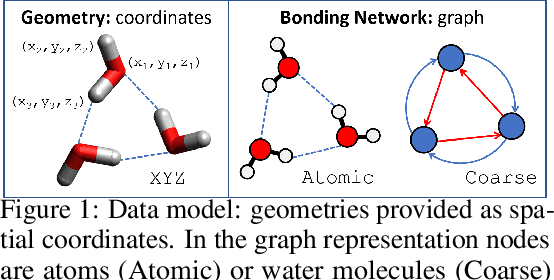
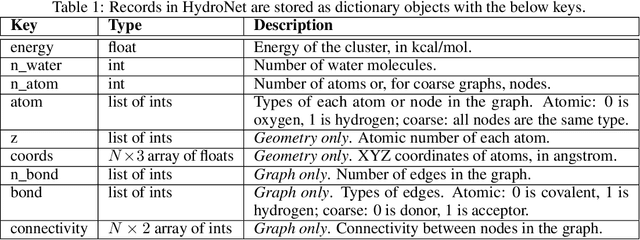
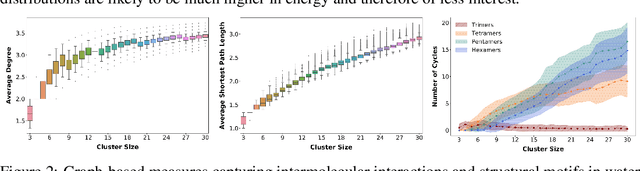
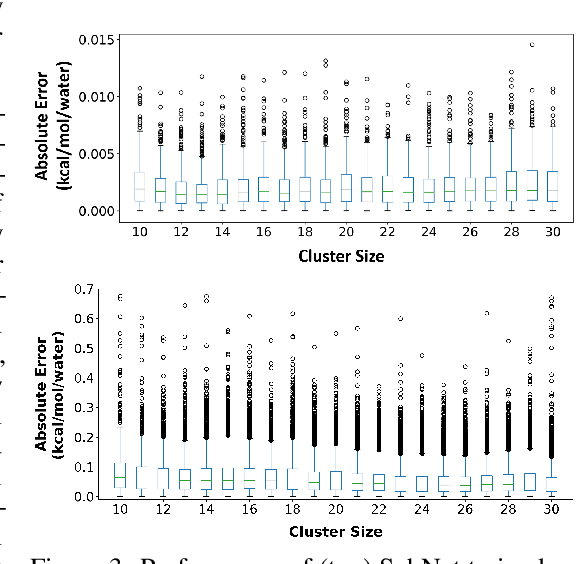
Intermolecular and long-range interactions are central to phenomena as diverse as gene regulation, topological states of quantum materials, electrolyte transport in batteries, and the universal solvation properties of water. We present a set of challenge problems for preserving intermolecular interactions and structural motifs in machine-learning approaches to chemical problems, through the use of a recently published dataset of 4.95 million water clusters held together by hydrogen bonding interactions and resulting in longer range structural patterns. The dataset provides spatial coordinates as well as two types of graph representations, to accommodate a variety of machine-learning practices.