A Comprehensive Review of Latent Space Dynamics Identification Algorithms for Intrusive and Non-Intrusive Reduced-Order-Modeling

Numerical solvers of partial differential equations (PDEs) have been widely employed for simulating physical systems. However, the computational cost remains a major bottleneck in various scientific and engineering applications, which has motivated the development of reduced-order models (ROMs). Recently, machine-learning-based ROMs have gained significant popularity and are promising for addressing some limitations of traditional ROM methods, especially for advection dominated systems. In this chapter, we focus on a particular framework known as Latent Space Dynamics Identification (LaSDI), which transforms the high-fidelity data, governed by a PDE, to simpler and low-dimensional latent-space data, governed by ordinary differential equations (ODEs). These ODEs can be learned and subsequently interpolated to make ROM predictions. Each building block of LaSDI can be easily modulated depending on the application, which makes the LaSDI framework highly flexible. In particular, we present strategies to enforce the laws of thermodynamics into LaSDI models (tLaSDI), enhance robustness in the presence of noise through the weak form (WLaSDI), select high-fidelity training data efficiently through active learning (gLaSDI, GPLaSDI), and quantify the ROM prediction uncertainty through Gaussian processes (GPLaSDI). We demonstrate the performance of different LaSDI approaches on Burgers equation, a non-linear heat conduction problem, and a plasma physics problem, showing that LaSDI algorithms can achieve relative errors of less than a few percent and up to thousands of times speed-ups.

tLaSDI: Thermodynamics-informed latent space dynamics identification

We propose a data-driven latent space dynamics identification method (tLaSDI) that embeds the first and second principles of thermodynamics. The latent variables are learned through an autoencoder as a nonlinear dimension reduction model. The dynamics of the latent variables are constructed by a neural network-based model that preserves certain structures to respect the thermodynamic laws through the GENERIC formalism. An abstract error estimate of the approximation is established, which provides a new loss formulation involving the Jacobian computation of autoencoder. Both the autoencoder and the latent dynamics are trained to minimize the new loss. Numerical examples are presented to demonstrate the performance of tLaSDI, which exhibits robust generalization ability, even in extrapolation. In addition, an intriguing correlation is empirically observed between the entropy production rates in the latent space and the behaviors of the full-state solution.

Deep Multiscale Model Learning

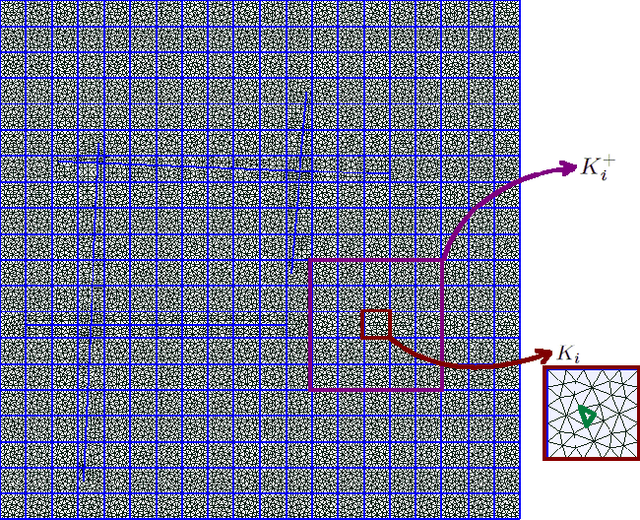
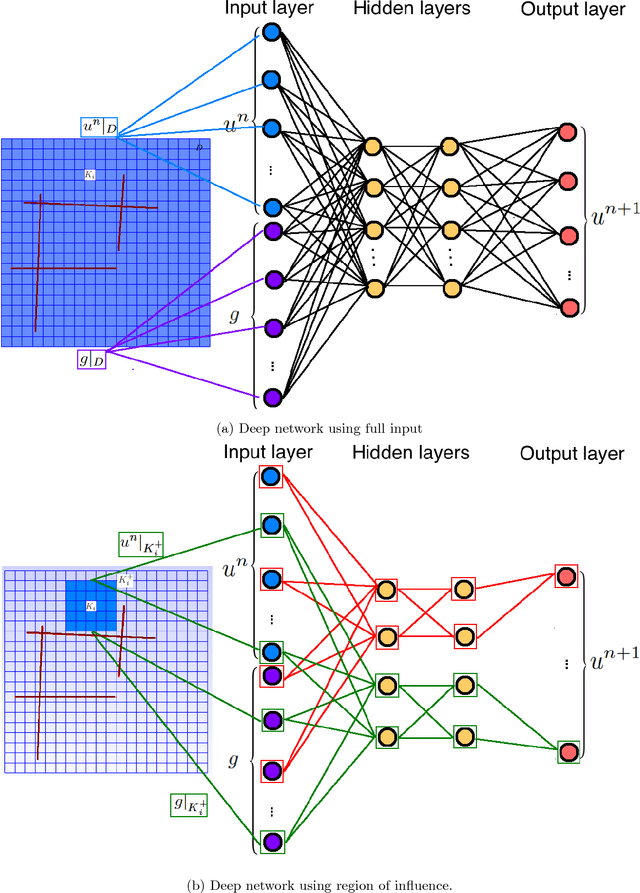
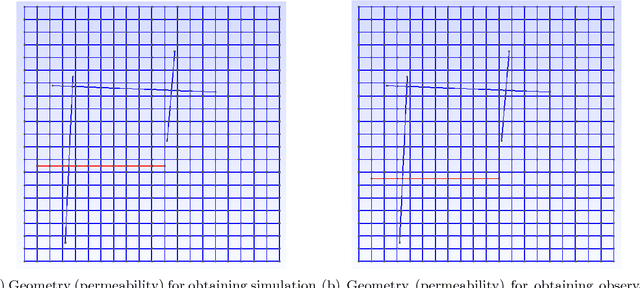
The objective of this paper is to design novel multi-layer neural network architectures for multiscale simulations of flows taking into account the observed data and physical modeling concepts. Our approaches use deep learning concepts combined with local multiscale model reduction methodologies to predict flow dynamics. Using reduced-order model concepts is important for constructing robust deep learning architectures since the reduced-order models provide fewer degrees of freedom. Flow dynamics can be thought of as multi-layer networks. More precisely, the solution (e.g., pressures and saturations) at the time instant $n+1$ depends on the solution at the time instant $n$ and input parameters, such as permeability fields, forcing terms, and initial conditions. One can regard the solution as a multi-layer network, where each layer, in general, is a nonlinear forward map and the number of layers relates to the internal time steps. We will rely on rigorous model reduction concepts to define unknowns and connections for each layer. In each layer, our reduced-order models will provide a forward map, which will be modified ("trained") using available data. It is critical to use reduced-order models for this purpose, which will identify the regions of influence and the appropriate number of variables. Because of the lack of available data, the training will be supplemented with computational data as needed and the interpolation between data-rich and data-deficient models. We will also use deep learning algorithms to train the elements of the reduced model discrete system. We will present main ingredients of our approach and numerical results. Numerical results show that using deep learning and multiscale models, we can improve the forward models, which are conditioned to the available data.