Defining Foundation Models for Computational Science: A Call for Clarity and Rigor

The widespread success of foundation models in natural language processing and computer vision has inspired researchers to extend the concept to scientific machine learning and computational science. However, this position paper argues that as the term "foundation model" is an evolving concept, its application in computational science is increasingly used without a universally accepted definition, potentially creating confusion and diluting its precise scientific meaning. In this paper, we address this gap by proposing a formal definition of foundation models in computational science, grounded in the core values of generality, reusability, and scalability. We articulate a set of essential and desirable characteristics that such models must exhibit, drawing parallels with traditional foundational methods, like the finite element and finite volume methods. Furthermore, we introduce the Data-Driven Finite Element Method (DD-FEM), a framework that fuses the modular structure of classical FEM with the representational power of data-driven learning. We demonstrate how DD-FEM addresses many of the key challenges in realizing foundation models for computational science, including scalability, adaptability, and physics consistency. By bridging traditional numerical methods with modern AI paradigms, this work provides a rigorous foundation for evaluating and developing novel approaches toward future foundation models in computational science.

Efficient nonlinear manifold reduced order model

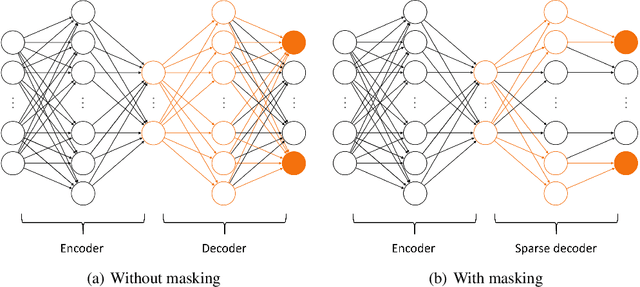
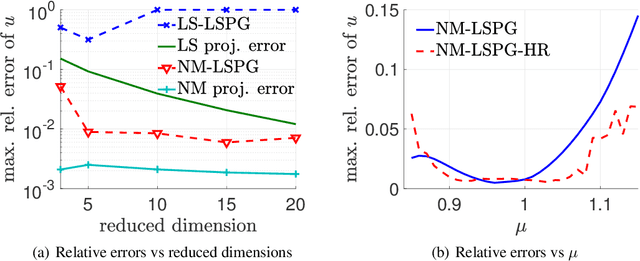
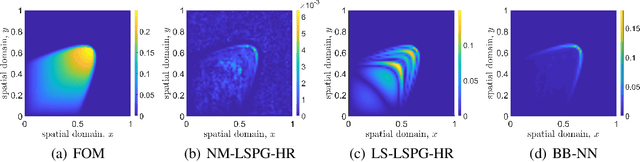
Traditional linear subspace reduced order models (LS-ROMs) are able to accelerate physical simulations, in which the intrinsic solution space falls into a subspace with a small dimension, i.e., the solution space has a small Kolmogorov n-width. However, for physical phenomena not of this type, such as advection-dominated flow phenomena, a low-dimensional linear subspace poorly approximates the solution. To address cases such as these, we have developed an efficient nonlinear manifold ROM (NM-ROM), which can better approximate high-fidelity model solutions with a smaller latent space dimension than the LS-ROMs. Our method takes advantage of the existing numerical methods that are used to solve the corresponding full order models (FOMs). The efficiency is achieved by developing a hyper-reduction technique in the context of the NM-ROM. Numerical results show that neural networks can learn a more efficient latent space representation on advection-dominated data from 2D Burgers' equations with a high Reynolds number. A speed-up of up to 11.7 for 2D Burgers' equations is achieved with an appropriate treatment of the nonlinear terms through a hyper-reduction technique.

A fast and accurate physics-informed neural network reduced order model with shallow masked autoencoder

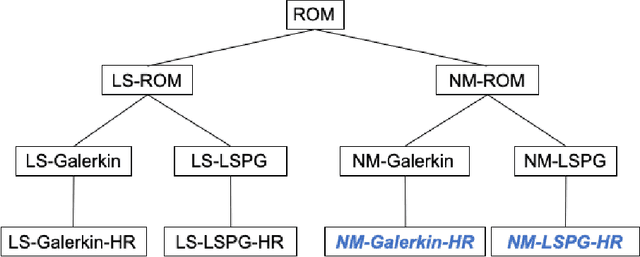
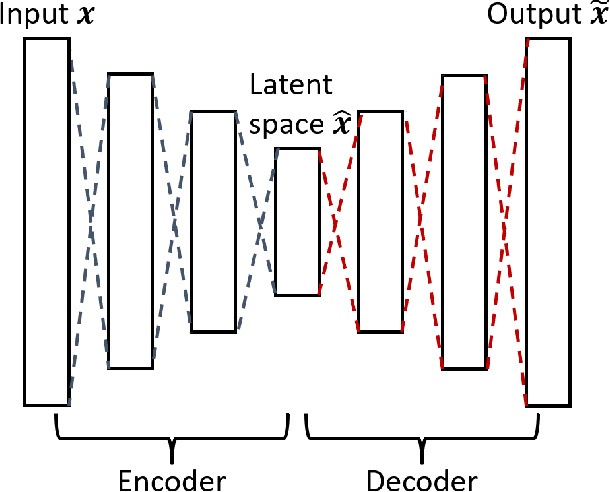
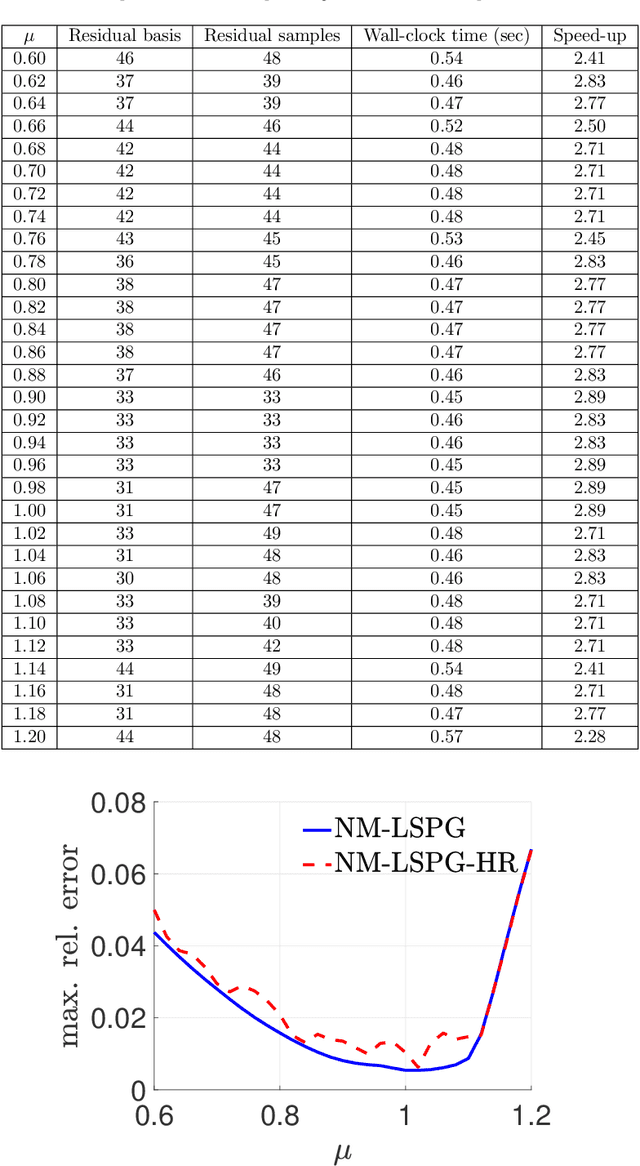
Traditional linear subspace reduced order models (LS-ROMs) are able to accelerate physical simulations, in which the intrinsic solution space falls into a subspace with a small dimension, i.e., the solution space has a small Kolmogorov n-width. However, for physical phenomena not of this type, e.g., any advection-dominated flow phenomena, such as in traffic flow, atmospheric flows, and air flow over vehicles, a low-dimensional linear subspace poorly approximates the solution. To address cases such as these, we have developed a fast and accurate physics-informed neural network ROM, namely nonlinear manifold ROM (NM-ROM), which can better approximate high-fidelity model solutions with a smaller latent space dimension than the LS-ROMs. Our method takes advantage of the existing numerical methods that are used to solve the corresponding full order models. The efficiency is achieved by developing a hyper-reduction technique in the context of the NM-ROM. Numerical results show that neural networks can learn a more efficient latent space representation on advection-dominated data from 1D and 2D Burgers' equations. A speedup of up to 2.6 for 1D Burgers' and a speedup of 11.7 for 2D Burgers' equations are achieved with an appropriate treatment of the nonlinear terms through a hyper-reduction technique. Finally, a posteriori error bounds for the NM-ROMs are derived that take account of the hyper-reduced operators.