Joint Cryo-ET Alignment and Reconstruction with Neural Deformation Fields

We propose a framework to jointly determine the deformation parameters and reconstruct the unknown volume in electron cryotomography (CryoET). CryoET aims to reconstruct three-dimensional biological samples from two-dimensional projections. A major challenge is that we can only acquire projections for a limited range of tilts, and that each projection undergoes an unknown deformation during acquisition. Not accounting for these deformations results in poor reconstruction. The existing CryoET software packages attempt to align the projections, often in a workflow which uses manual feedback. Our proposed method sidesteps this inconvenience by automatically computing a set of undeformed projections while simultaneously reconstructing the unknown volume. We achieve this by learning a continuous representation of the undeformed measurements and deformation parameters. We show that our approach enables the recovery of high-frequency details that are destroyed without accounting for deformations.

Differentiable Uncalibrated Imaging

We propose a differentiable imaging framework to address uncertainty in measurement coordinates such as sensor locations and projection angles. We formulate the problem as measurement interpolation at unknown nodes supervised through the forward operator. To solve it we apply implicit neural networks, also known as neural fields, which are naturally differentiable with respect to the input coordinates. We also develop differentiable spline interpolators which perform as well as neural networks, require less time to optimize and have well-understood properties. Differentiability is key as it allows us to jointly fit a measurement representation, optimize over the uncertain measurement coordinates, and perform image reconstruction which in turn ensures consistent calibration. We apply our approach to 2D and 3D computed tomography and show that it produces improved reconstructions compared to baselines that do not account for the lack of calibration. The flexibility of the proposed framework makes it easy to apply to almost arbitrary imaging problems.

Contour-guided Image Completion with Perceptual Grouping

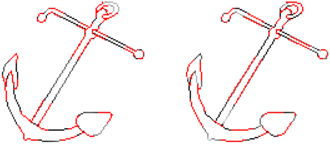
Humans are excellent at perceiving illusory outlines. We are readily able to complete contours, shapes, scenes, and even unseen objects when provided with images that contain broken fragments of a connected appearance. In vision science, this ability is largely explained by perceptual grouping: a foundational set of processes in human vision that describes how separated elements can be grouped. In this paper, we revisit an algorithm called Stochastic Completion Fields (SCFs) that mechanizes a set of such processes -- good continuity, closure, and proximity -- through contour completion. This paper implements a modernized model of the SCF algorithm, and uses it in an image editing framework where we propose novel methods to complete fragmented contours. We show how the SCF algorithm plausibly mimics results in human perception. We use the SCF completed contours as guides for inpainting, and show that our guides improve the performance of state-of-the-art models. Additionally, we show that the SCF aids in finding edges in high-noise environments. Overall, our described algorithms resemble an important mechanism in the human visual system, and offer a novel framework that modern computer vision models can benefit from.

Total least squares phase retrieval

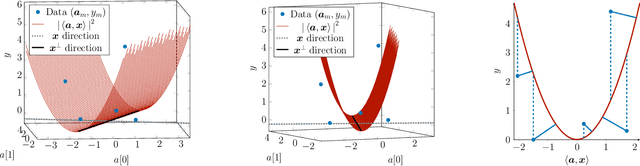
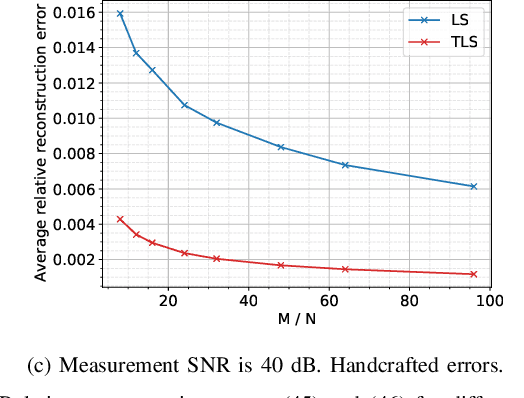
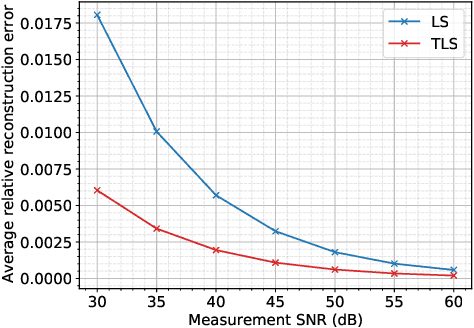
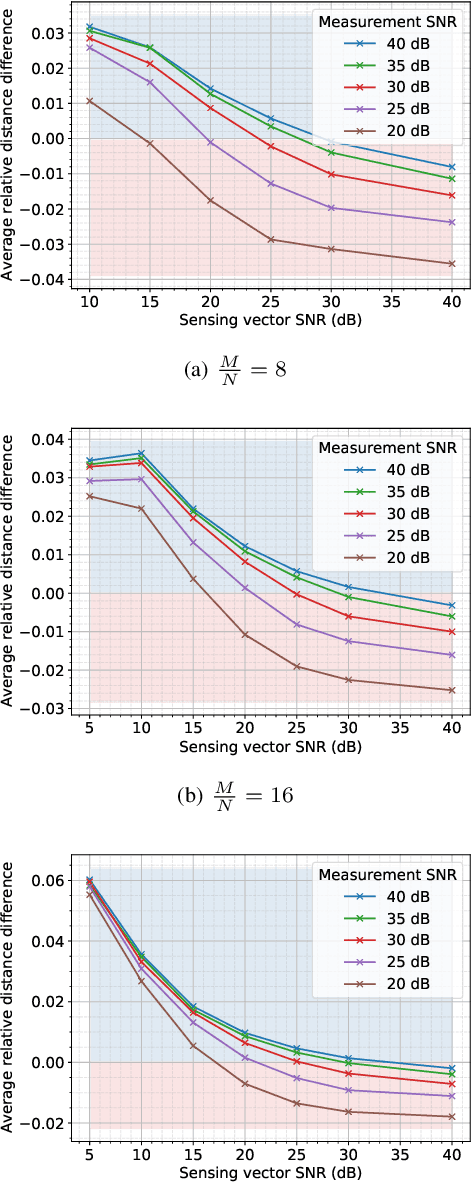
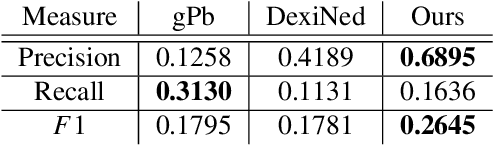
We address the phase retrieval problem with errors in the sensing vectors. A number of recent methods for phase retrieval are based on least squares (LS) formulations which assume errors in the quadratic measurements. We extend this approach to handle errors in the sensing vectors by adopting the total least squares (TLS) framework familiar from linear inverse problems with operator errors. We show how gradient descent and the peculiar geometry of the phase retrieval problem can be used to obtain a simple and efficient TLS solution. Additionally, we derive the gradients of the TLS and LS solutions with respect to the sensing vectors and measurements which enables us to calculate the solution errors. By analyzing these error expressions we determine when each method should perform well. We run simulations to demonstrate the benefits of our method and verify the analysis. We further demonstrate the effectiveness of our approach by performing phase retrieval experiments on real optical hardware which naturally contains sensing vector and measurement errors.

Improving the affordability of robustness training for DNNs

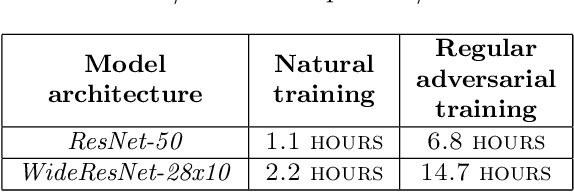
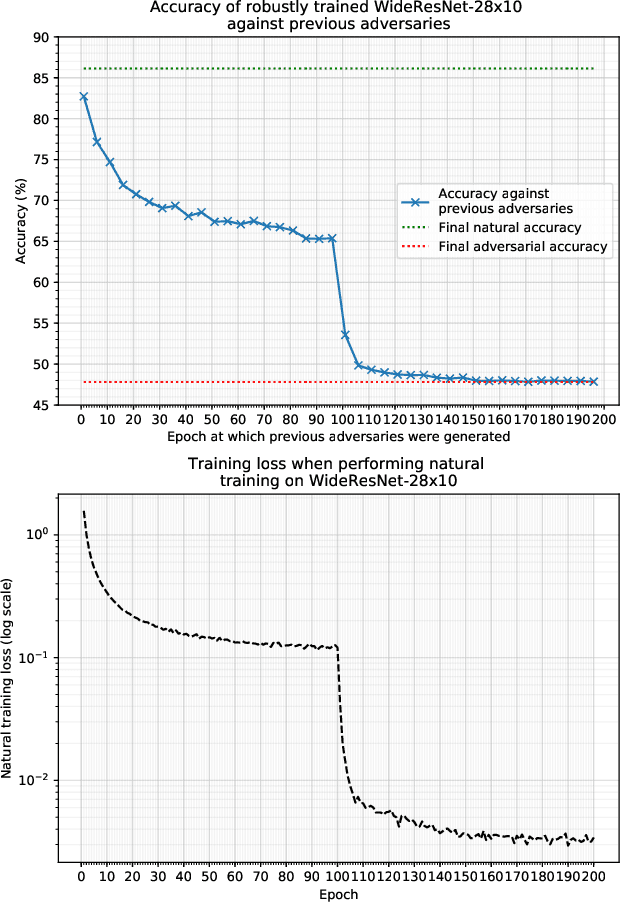
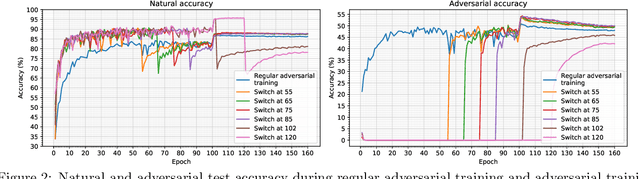
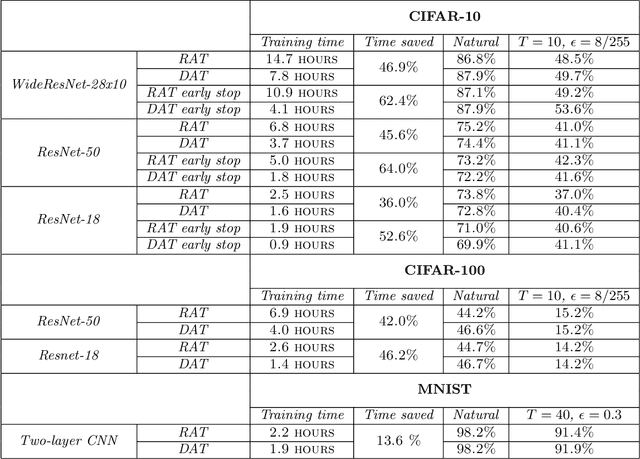
Projected Gradient Descent (PGD) based adversarial training has become one of the most prominent methods for building robust deep neural network models. However, the computational complexity associated with this approach, due to the maximization of the loss function when finding adversaries, is a longstanding problem and may be prohibitive when using larger and more complex models. In this paper, we propose a modification of the PGD method for adversarial training and demonstrate that models can be trained much more efficiently without any loss in accuracy on natural and adversarial samples. We argue that the initial phase of adversarial training is redundant and can be replaced with natural training thereby increasing the computational efficiency significantly. We support our argument with insights on the nature of the adversaries and their relative strength during the training process. We show that our proposed method can reduce the training time to up to 38\% of the original training time with comparable model accuracy and generalization on various strengths of adversarial attacks.

Don't take it lightly: Phasing optical random projections with unknown operators

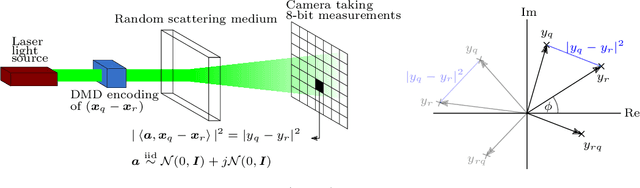
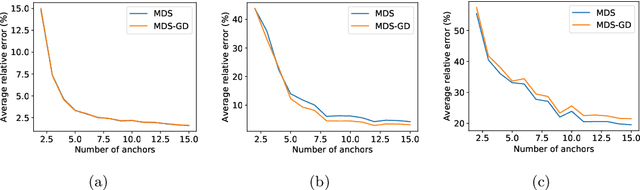
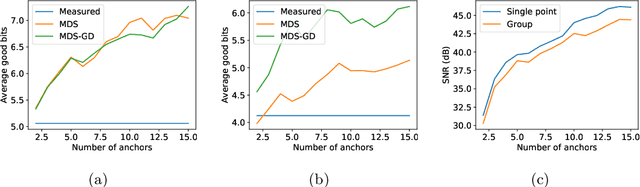
In this paper we tackle the problem of recovering the phase of complex linear measurements when only magnitude information is available and we control the input. We are motivated by the recent development of dedicated optics-based hardware for rapid random projections which leverages the propagation of light in random media. A signal of interest $\mathbf{\xi} \in \mathbb{R}^N$ is mixed by a random scattering medium to compute the projection $\mathbf{y} = \mathbf{A} \mathbf{\xi}$, with $\mathbf{A} \in \mathbb{C}^{M \times N}$ being a realization of a standard complex Gaussian iid random matrix. Two difficulties arise in this scheme: only the intensity ${|\mathbf{y}|}^2$ can be recorded by the camera, and the transmission matrix $\mathbf{A}$ is unknown. We show that even without knowing $\mathbf{A}$, we can recover the unknown phase of $\mathbf{y}$ for some equivalent transmission matrix with the same distribution as $\mathbf{A}$. Our method is based on two observations: first, changing the phase of any row of $\mathbf{A}$ does not change its distribution; and second, since we control the input we can interfere $\mathbf{\xi}$ with arbitrary reference signals. We show how to leverage these observations to cast the measurement phase retrieval problem as a Euclidean distance geometry problem. We demonstrate appealing properties of the proposed algorithm on both numerical simulations and in real hardware experiments. Not only does our algorithm accurately recover the missing phase, but it mitigates the effects of quantization and the sensitivity threshold, thus also improving the measured magnitudes.

Random mesh projectors for inverse problems

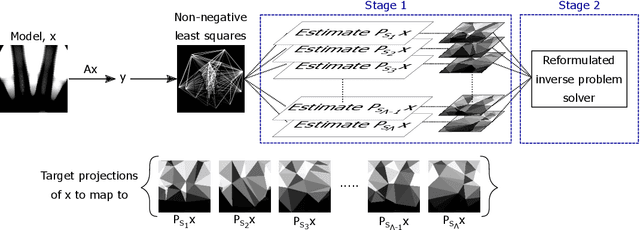
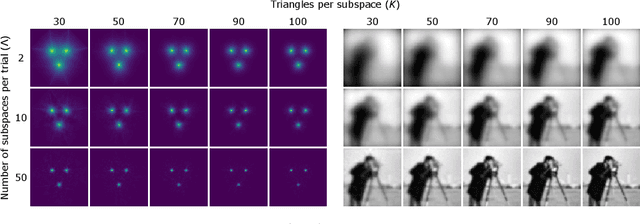
We propose a new learning-based approach to solve ill-posed inverse problems in imaging. We address the case where ground truth training samples are rare and the problem is severely ill-posed - both because of the underlying physics and because we can only get few measurements. This setting is common in geophysical imaging and remote sensing. We show that in this case the common approach to directly learn the mapping from the measured data to the reconstruction becomes unstable. Instead, we propose to first learn an ensemble of simpler mappings from the data to projections of the unknown image into random piecewise-constant subspaces. We then combine the projections to form a final reconstruction by solving a deconvolution-like problem. We show experimentally the proposed method is more robust to measurement noise and corruptions not seen during training than a directly learned inverse.