HEIST: A Graph Foundation Model for Spatial Transcriptomics and Proteomics Data

Single-cell transcriptomics has become a great source for data-driven insights into biology, enabling the use of advanced deep learning methods to understand cellular heterogeneity and transcriptional regulation at the single-cell level. With the advent of spatial transcriptomics data we have the promise of learning about cells within a tissue context as it provides both spatial coordinates and transcriptomic readouts. However, existing models either ignore spatial resolution or the gene regulatory information. Gene regulation in cells can change depending on microenvironmental cues from neighboring cells, but existing models neglect gene regulatory patterns with hierarchical dependencies across levels of abstraction. In order to create contextualized representations of cells and genes from spatial transcriptomics data, we introduce HEIST, a hierarchical graph transformer-based foundation model for spatial transcriptomics and proteomics data. HEIST models tissue as spatial cellular neighborhood graphs, and each cell is, in turn, modeled as a gene regulatory network graph. The framework includes a hierarchical graph transformer that performs cross-level message passing and message passing within levels. HEIST is pre-trained on 22.3M cells from 124 tissues across 15 organs using spatially-aware contrastive learning and masked auto-encoding objectives. Unsupervised analysis of HEIST representations of cells, shows that it effectively encodes the microenvironmental influences in cell embeddings, enabling the discovery of spatially-informed subpopulations that prior models fail to differentiate. Further, HEIST achieves state-of-the-art results on four downstream task such as clinical outcome prediction, cell type annotation, gene imputation, and spatially-informed cell clustering across multiple technologies, highlighting the importance of hierarchical modeling and GRN-based representations.

HiPoNet: A Topology-Preserving Multi-View Neural Network For High Dimensional Point Cloud and Single-Cell Data

In this paper, we propose HiPoNet, an end-to-end differentiable neural network for regression, classification, and representation learning on high-dimensional point clouds. Single-cell data can have high dimensionality exceeding the capabilities of existing methods point cloud tailored for 3D data. Moreover, modern single-cell and spatial experiments now yield entire cohorts of datasets (i.e. one on every patient), necessitating models that can process large, high-dimensional point clouds at scale. Most current approaches build a single nearest-neighbor graph, discarding important geometric information. In contrast, HiPoNet forms higher-order simplicial complexes through learnable feature reweighting, generating multiple data views that disentangle distinct biological processes. It then employs simplicial wavelet transforms to extract multi-scale features - capturing both local and global topology. We empirically show that these components preserve topological information in the learned representations, and that HiPoNet significantly outperforms state-of-the-art point-cloud and graph-based models on single cell. We also show an application of HiPoNet on spatial transcriptomics datasets using spatial co-ordinates as one of the views. Overall, HiPoNet offers a robust and scalable solution for high-dimensional data analysis.

Exploring the Manifold of Neural Networks Using Diffusion Geometry

Drawing motivation from the manifold hypothesis, which posits that most high-dimensional data lies on or near low-dimensional manifolds, we apply manifold learning to the space of neural networks. We learn manifolds where datapoints are neural networks by introducing a distance between the hidden layer representations of the neural networks. These distances are then fed to the non-linear dimensionality reduction algorithm PHATE to create a manifold of neural networks. We characterize this manifold using features of the representation, including class separation, hierarchical cluster structure, spectral entropy, and topological structure. Our analysis reveals that high-performing networks cluster together in the manifold, displaying consistent embedding patterns across all these features. Finally, we demonstrate the utility of this approach for guiding hyperparameter optimization and neural architecture search by sampling from the manifold.

ProtSCAPE: Mapping the landscape of protein conformations in molecular dynamics

Understanding the dynamic nature of protein structures is essential for comprehending their biological functions. While significant progress has been made in predicting static folded structures, modeling protein motions on microsecond to millisecond scales remains challenging. To address these challenges, we introduce a novel deep learning architecture, Protein Transformer with Scattering, Attention, and Positional Embedding (ProtSCAPE), which leverages the geometric scattering transform alongside transformer-based attention mechanisms to capture protein dynamics from molecular dynamics (MD) simulations. ProtSCAPE utilizes the multi-scale nature of the geometric scattering transform to extract features from protein structures conceptualized as graphs and integrates these features with dual attention structures that focus on residues and amino acid signals, generating latent representations of protein trajectories. Furthermore, ProtSCAPE incorporates a regression head to enforce temporally coherent latent representations.

Convergence of Manifold Filter-Combine Networks

In order to better understand manifold neural networks (MNNs), we introduce Manifold Filter-Combine Networks (MFCNs). The filter-combine framework parallels the popular aggregate-combine paradigm for graph neural networks (GNNs) and naturally suggests many interesting families of MNNs which can be interpreted as the manifold analog of various popular GNNs. We then propose a method for implementing MFCNs on high-dimensional point clouds that relies on approximating the manifold by a sparse graph. We prove that our method is consistent in the sense that it converges to a continuum limit as the number of data points tends to infinity.

Geometric Scattering on Measure Spaces

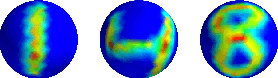
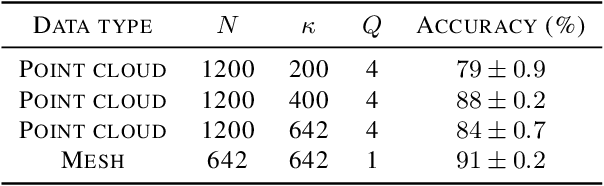
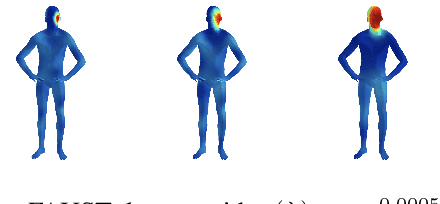
The scattering transform is a multilayered, wavelet-based transform initially introduced as a model of convolutional neural networks (CNNs) that has played a foundational role in our understanding of these networks' stability and invariance properties. Subsequently, there has been widespread interest in extending the success of CNNs to data sets with non-Euclidean structure, such as graphs and manifolds, leading to the emerging field of geometric deep learning. In order to improve our understanding of the architectures used in this new field, several papers have proposed generalizations of the scattering transform for non-Euclidean data structures such as undirected graphs and compact Riemannian manifolds without boundary. In this paper, we introduce a general, unified model for geometric scattering on measure spaces. Our proposed framework includes previous work on geometric scattering as special cases but also applies to more general settings such as directed graphs, signed graphs, and manifolds with boundary. We propose a new criterion that identifies to which groups a useful representation should be invariant and show that this criterion is sufficient to guarantee that the scattering transform has desirable stability and invariance properties. Additionally, we consider finite measure spaces that are obtained from randomly sampling an unknown manifold. We propose two methods for constructing a data-driven graph on which the associated graph scattering transform approximates the scattering transform on the underlying manifold. Moreover, we use a diffusion-maps based approach to prove quantitative estimates on the rate of convergence of one of these approximations as the number of sample points tends to infinity. Lastly, we showcase the utility of our method on spherical images, directed graphs, and on high-dimensional single-cell data.

The Manifold Scattering Transform for High-Dimensional Point Cloud Data

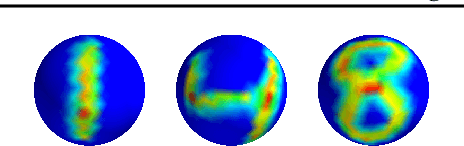
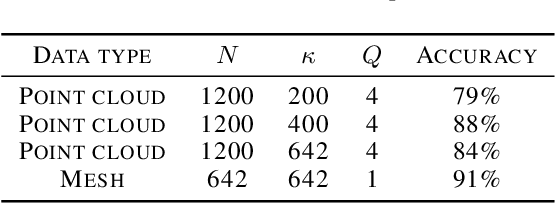
The manifold scattering transform is a deep feature extractor for data defined on a Riemannian manifold. It is one of the first examples of extending convolutional neural network-like operators to general manifolds. The initial work on this model focused primarily on its theoretical stability and invariance properties but did not provide methods for its numerical implementation except in the case of two-dimensional surfaces with predefined meshes. In this work, we present practical schemes, based on the theory of diffusion maps, for implementing the manifold scattering transform to datasets arising in naturalistic systems, such as single cell genetics, where the data is a high-dimensional point cloud modeled as lying on a low-dimensional manifold. We show that our methods are effective for signal classification and manifold classification tasks.