Retentive Neural Quantum States: Efficient Ansätze for Ab Initio Quantum Chemistry

Neural-network quantum states (NQS) has emerged as a powerful application of quantum-inspired deep learning for variational Monte Carlo methods, offering a competitive alternative to existing techniques for identifying ground states of quantum problems. A significant advancement toward improving the practical scalability of NQS has been the incorporation of autoregressive models, most recently transformers, as variational ansatze. Transformers learn sequence information with greater expressiveness than recurrent models, but at the cost of increased time complexity with respect to sequence length. We explore the use of the retentive network (RetNet), a recurrent alternative to transformers, as an ansatz for solving electronic ground state problems in $\textit{ab initio}$ quantum chemistry. Unlike transformers, RetNets overcome this time complexity bottleneck by processing data in parallel during training, and recurrently during inference. We give a simple computational cost estimate of the RetNet and directly compare it with similar estimates for transformers, establishing a clear threshold ratio of problem-to-model size past which the RetNet's time complexity outperforms that of the transformer. Though this efficiency can comes at the expense of decreased expressiveness relative to the transformer, we overcome this gap through training strategies that leverage the autoregressive structure of the model -- namely, variational neural annealing. Our findings support the RetNet as a means of improving the time complexity of NQS without sacrificing accuracy. We provide further evidence that the ablative improvements of neural annealing extend beyond the RetNet architecture, suggesting it would serve as an effective general training strategy for autoregressive NQS.

Toward Neural Network Simulation of Variational Quantum Algorithms

Variational quantum algorithms (VQAs) utilize a hybrid quantum-classical architecture to recast problems of high-dimensional linear algebra as ones of stochastic optimization. Despite the promise of leveraging near- to intermediate-term quantum resources to accelerate this task, the computational advantage of VQAs over wholly classical algorithms has not been firmly established. For instance, while the variational quantum eigensolver (VQE) has been developed to approximate low-lying eigenmodes of high-dimensional sparse linear operators, analogous classical optimization algorithms exist in the variational Monte Carlo (VMC) literature, utilizing neural networks in place of quantum circuits to represent quantum states. In this paper we ask if classical stochastic optimization algorithms can be constructed paralleling other VQAs, focusing on the example of the variational quantum linear solver (VQLS). We find that such a construction can be applied to the VQLS, yielding a paradigm that could theoretically extend to other VQAs of similar form.

Scalable neural quantum states architecture for quantum chemistry

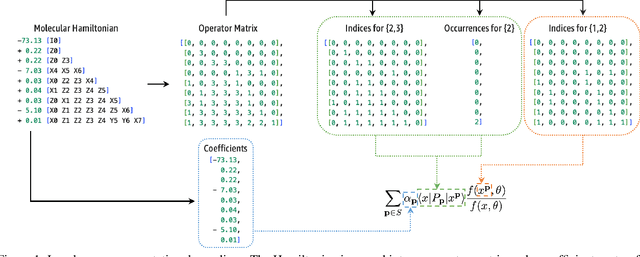
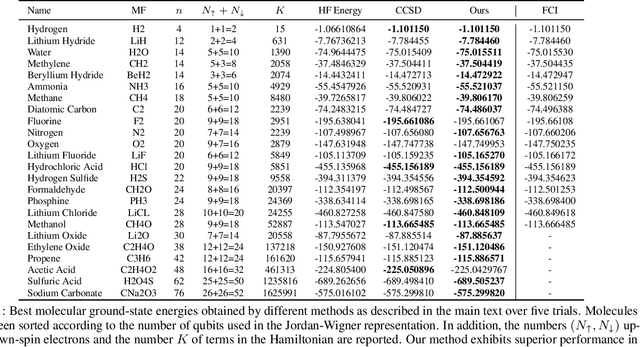
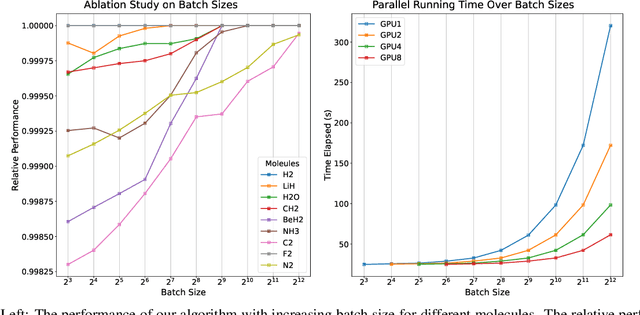
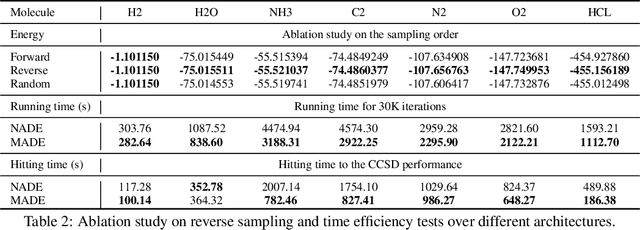
Variational optimization of neural-network representations of quantum states has been successfully applied to solve interacting fermionic problems. Despite rapid developments, significant scalability challenges arise when considering molecules of large scale, which correspond to non-locally interacting quantum spin Hamiltonians consisting of sums of thousands or even millions of Pauli operators. In this work, we introduce scalable parallelization strategies to improve neural-network-based variational quantum Monte Carlo calculations for ab-initio quantum chemistry applications. We establish GPU-supported local energy parallelism to compute the optimization objective for Hamiltonians of potentially complex molecules. Using autoregressive sampling techniques, we demonstrate systematic improvement in wall-clock timings required to achieve CCSD baseline target energies. The performance is further enhanced by accommodating the structure of resultant spin Hamiltonians into the autoregressive sampling ordering. The algorithm achieves promising performance in comparison with the classical approximate methods and exhibits both running time and scalability advantages over existing neural-network based methods.

Numerical and geometrical aspects of flow-based variational quantum Monte Carlo

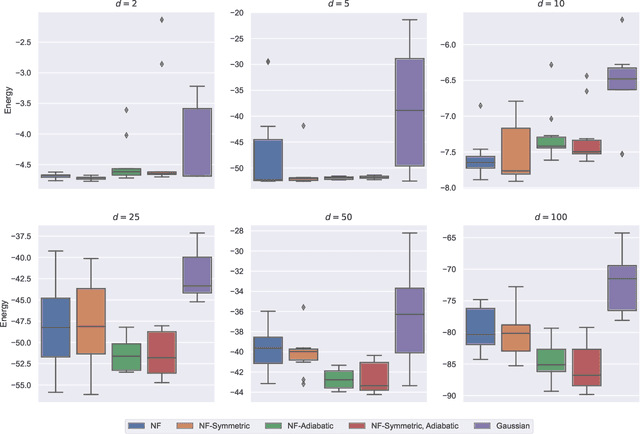
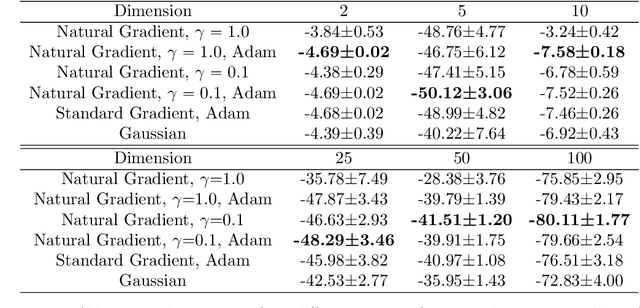
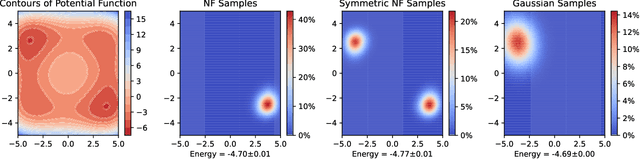
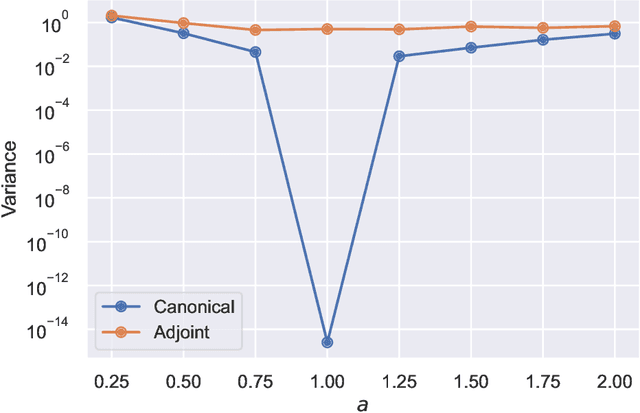
This article aims to summarize recent and ongoing efforts to simulate continuous-variable quantum systems using flow-based variational quantum Monte Carlo techniques, focusing for pedagogical purposes on the example of bosons in the field amplitude (quadrature) basis. Particular emphasis is placed on the variational real- and imaginary-time evolution problems, carefully reviewing the stochastic estimation of the time-dependent variational principles and their relationship with information geometry. Some practical instructions are provided to guide the implementation of a PyTorch code. The review is intended to be accessible to researchers interested in machine learning and quantum information science.

Continuous-variable neural-network quantum states and the quantum rotor model

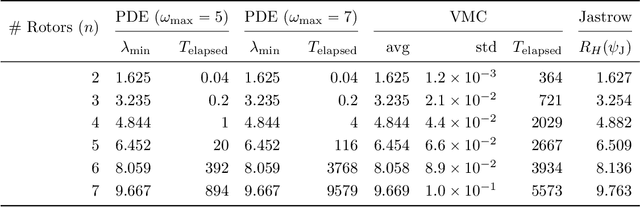
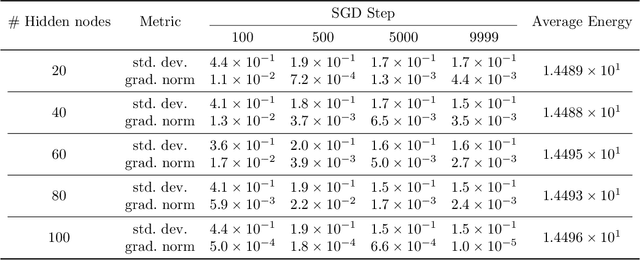
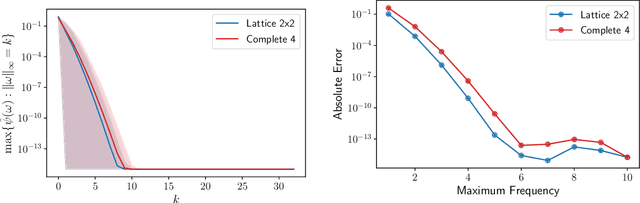
We initiate the study of neural-network quantum state algorithms for analyzing continuous-variable lattice quantum systems in first quantization. A simple family of continuous-variable trial wavefunctons is introduced which naturally generalizes the restricted Boltzmann machine (RBM) wavefunction introduced for analyzing quantum spin systems. By virtue of its simplicity, the same variational Monte Carlo training algorithms that have been developed for ground state determination and time evolution of spin systems have natural analogues in the continuum. We offer a proof of principle demonstration in the context of ground state determination of a stoquastic quantum rotor Hamiltonian. Results are compared against those obtained from partial differential equation (PDE) based scalable eigensolvers. This study serves as a benchmark against which future investigation of continuous-variable neural quantum states can be compared, and points to the need to consider deep network architectures and more sophisticated training algorithms.

Meta Variational Monte Carlo

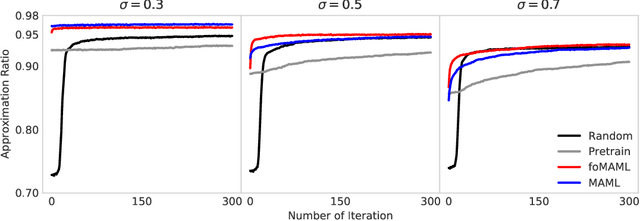
An identification is found between meta-learning and the problem of determining the ground state of a randomly generated Hamiltonian drawn from a known ensemble. A model-agnostic meta-learning approach is proposed to solve the associated learning problem and a preliminary experimental study of random Max-Cut problems indicates that the resulting Meta Variational Monte Carlo accelerates training and improves convergence.

Natural evolution strategies and quantum approximate optimization

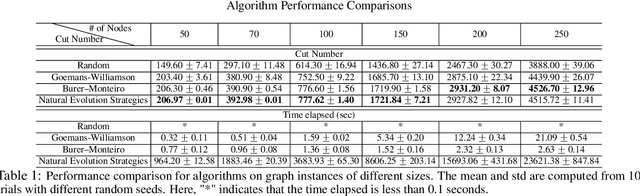
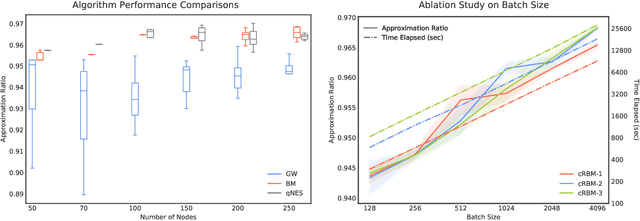
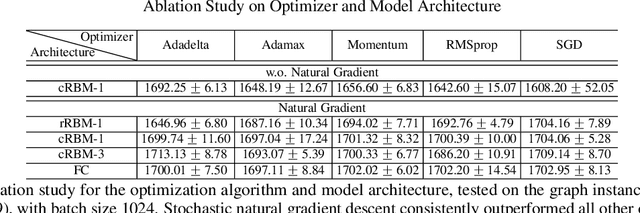
A notion of quantum natural evolution strategies is introduced, which provides a geometric synthesis of a number of known quantum/classical algorithms for performing classical black-box optimization. Recent work of Gomes et al. [2019] on combinatorial optimization using neural quantum states is pedagogically reviewed in this context, emphasizing the connection with natural evolution strategies. The algorithmic framework is illustrated for approximate combinatorial optimization problems, and a systematic strategy is found for improving the approximation ratios. In particular it is found that natural evolution strategies can achieve state-of-art approximation ratios for Max-Cut, at the expense of increased computation time.

An Active Learning Framework for Constructing High-fidelity Mobility Maps

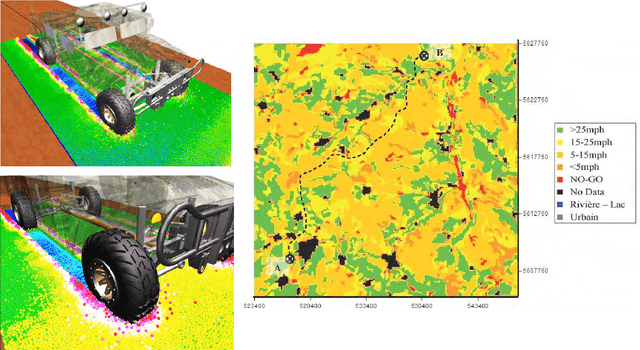
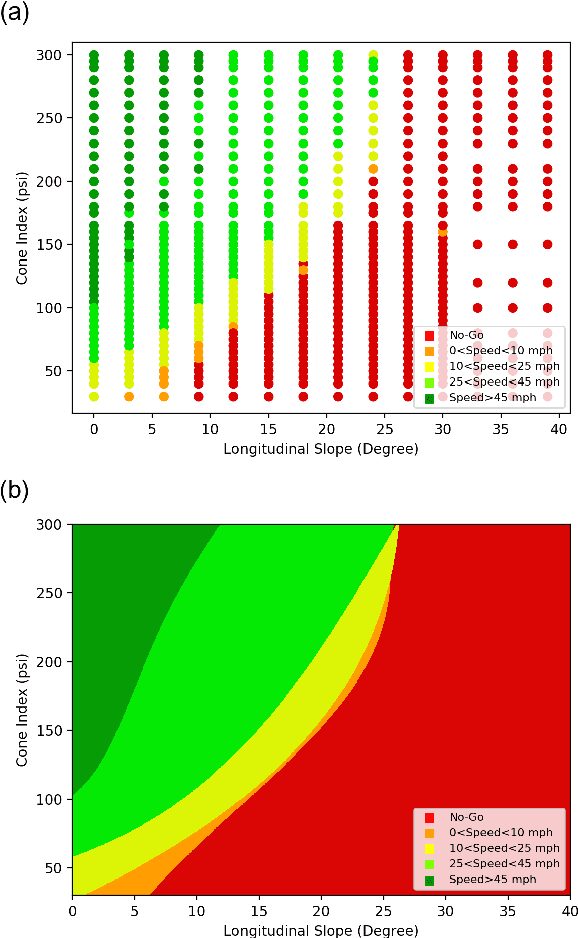
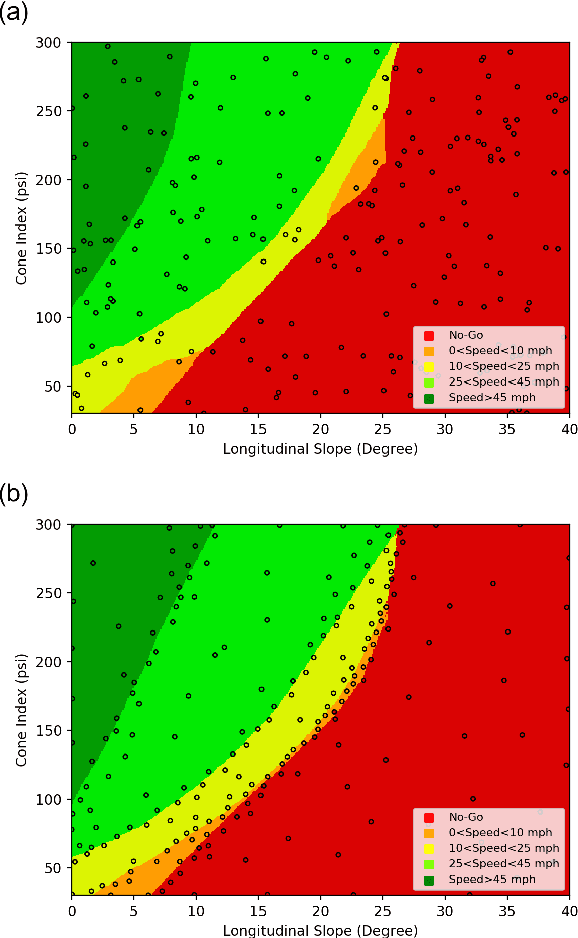
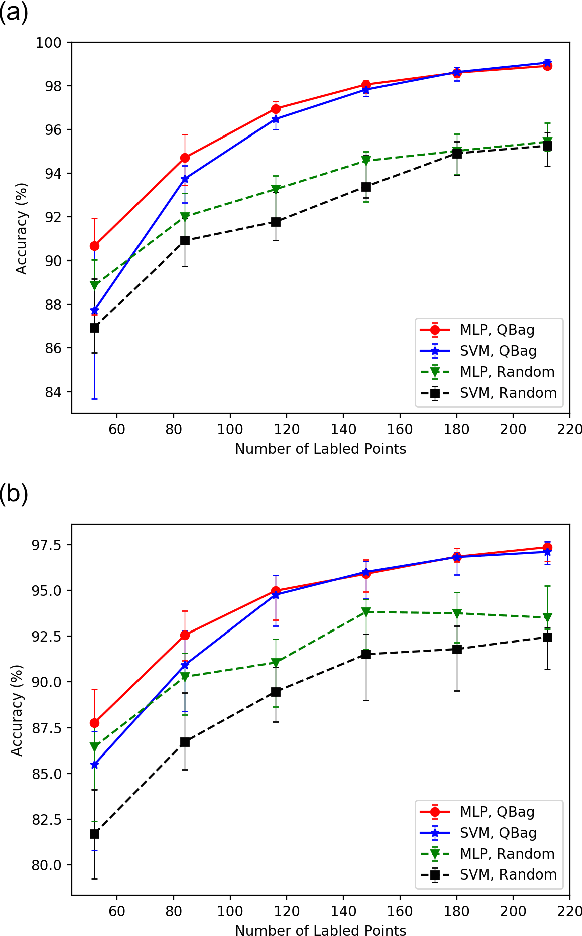
A mobility map, which provides maximum achievable speed on a given terrain, is essential for path planning of autonomous ground vehicles in off-road settings. While physics-based simulations play a central role in creating next-generation, high-fidelity mobility maps, they are cumbersome and expensive. For instance, a typical simulation can take weeks to run on a supercomputer and each map requires thousands of such simulations. Recent work at the U.S. Army CCDC Ground Vehicle Systems Center has shown that trained machine learning classifiers can greatly improve the efficiency of this process. However, deciding which simulations to run in order to train the classifier efficiently is still an open problem. According to PAC learning theory, data that can be separated by a classifier is expected to require $\mathcal{O}(1/\epsilon)$ randomly selected points (simulations) to train the classifier with error less than $\epsilon$. In this paper, building on existing algorithms, we introduce an active learning paradigm that substantially reduces the number of simulations needed to train a machine learning classifier without sacrificing accuracy. Experimental results suggest that our sampling algorithm can train a neural network, with higher accuracy, using less than half the number of simulations when compared to random sampling.