Best-Arm Identification-Based Trust Region Selection for Bayesian Optimization on Multimodal Functions

Gaussian process-based Bayesian optimization (BO) is a popular approach for expensive black-box optimization, but its performance often degrades on complex multimodal or high-dimensional problems. Trust region-based BO mitigates this issue by focusing on local regions, and recent studies suggest that selecting an effective region can be formulated as a multi-armed bandit problem. We propose a trajectory-aware framework that integrates best-arm identification (BAI) with trust region-based BO to efficiently solve multimodal optimization problems. Our method extrapolates the optimization trajectories of multiple locally initialized optimizers to predict their final performance and progressively eliminates suboptimal candidates via BAI. We theoretically show that the proposed BAI-guided BO converges faster to the global optimum than conventional BO under mild assumptions, and demonstrate its effectiveness through extensive experiments on synthetic and real-world benchmarks.

Adaptive LLM Routing under Budget Constraints

Large Language Models (LLMs) have revolutionized natural language processing, but their varying capabilities and costs pose challenges in practical applications. LLM routing addresses this by dynamically selecting the most suitable LLM for each query/task. Previous approaches treat this as a supervised learning problem, assuming complete knowledge of optimal query-LLM pairings. However, real-world scenarios lack such comprehensive mappings and face evolving user queries. We thus propose to study LLM routing as a contextual bandit problem, enabling adaptive decision-making using bandit feedback without requiring exhaustive inference across all LLMs for all queries (in contrast to supervised routing). To address this problem, we develop a shared embedding space for queries and LLMs, where query and LLM embeddings are aligned to reflect their affinity. This space is initially learned from offline human preference data and refined through online bandit feedback. We instantiate this idea through Preference-prior Informed Linucb fOr adaptive rouTing (PILOT), a novel extension of LinUCB. To handle diverse user budgets for model routing, we introduce an online cost policy modeled as a multi-choice knapsack problem, ensuring resource-efficient routing.

Regional Expected Improvement for Efficient Trust Region Selection in High-Dimensional Bayesian Optimization

Real-world optimization problems often involve complex objective functions with costly evaluations. While Bayesian optimization (BO) with Gaussian processes is effective for these challenges, it suffers in high-dimensional spaces due to performance degradation from limited function evaluations. To overcome this, simplification techniques like dimensionality reduction have been employed, yet they often rely on assumptions about the problem characteristics, potentially underperforming when these assumptions do not hold. Trust-region-based methods, which avoid such assumptions, focus on local search but risk stagnation in local optima. In this study, we propose a novel acquisition function, regional expected improvement (REI), designed to enhance trust-region-based BO in medium to high-dimensional settings. REI identifies regions likely to contain the global optimum, improving performance without relying on specific problem characteristics. We provide a theoretical proof that REI effectively identifies optimal trust regions and empirically demonstrate that incorporating REI into trust-region-based BO outperforms conventional BO and other high-dimensional BO methods in medium to high-dimensional real-world problems.

Selective Mixup Fine-Tuning for Optimizing Non-Decomposable Objectives

The rise in internet usage has led to the generation of massive amounts of data, resulting in the adoption of various supervised and semi-supervised machine learning algorithms, which can effectively utilize the colossal amount of data to train models. However, before deploying these models in the real world, these must be strictly evaluated on performance measures like worst-case recall and satisfy constraints such as fairness. We find that current state-of-the-art empirical techniques offer sub-optimal performance on these practical, non-decomposable performance objectives. On the other hand, the theoretical techniques necessitate training a new model from scratch for each performance objective. To bridge the gap, we propose SelMix, a selective mixup-based inexpensive fine-tuning technique for pre-trained models, to optimize for the desired objective. The core idea of our framework is to determine a sampling distribution to perform a mixup of features between samples from particular classes such that it optimizes the given objective. We comprehensively evaluate our technique against the existing empirical and theoretically principled methods on standard benchmark datasets for imbalanced classification. We find that proposed SelMix fine-tuning significantly improves the performance for various practical non-decomposable objectives across benchmarks.

Cost-Sensitive Self-Training for Optimizing Non-Decomposable Metrics

Self-training based semi-supervised learning algorithms have enabled the learning of highly accurate deep neural networks, using only a fraction of labeled data. However, the majority of work on self-training has focused on the objective of improving accuracy, whereas practical machine learning systems can have complex goals (e.g. maximizing the minimum of recall across classes, etc.) that are non-decomposable in nature. In this work, we introduce the Cost-Sensitive Self-Training (CSST) framework which generalizes the self-training-based methods for optimizing non-decomposable metrics. We prove that our framework can better optimize the desired non-decomposable metric utilizing unlabeled data, under similar data distribution assumptions made for the analysis of self-training. Using the proposed CSST framework, we obtain practical self-training methods (for both vision and NLP tasks) for optimizing different non-decomposable metrics using deep neural networks. Our results demonstrate that CSST achieves an improvement over the state-of-the-art in majority of the cases across datasets and objectives.

Causality-Aware Neighborhood Methods for Recommender Systems

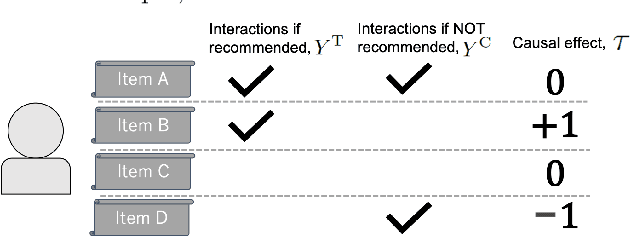
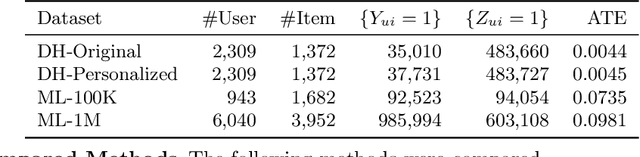
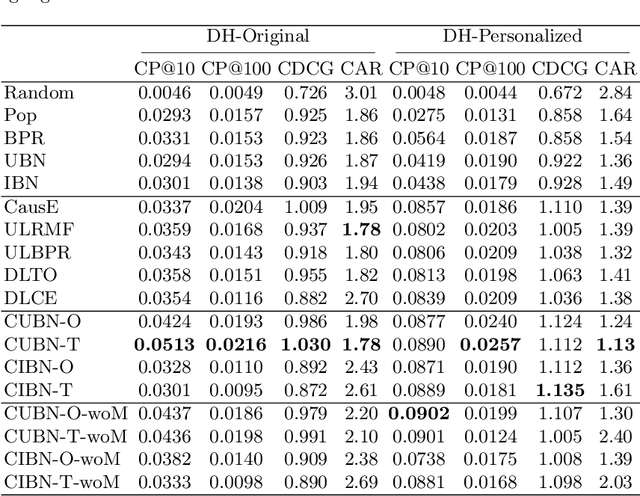
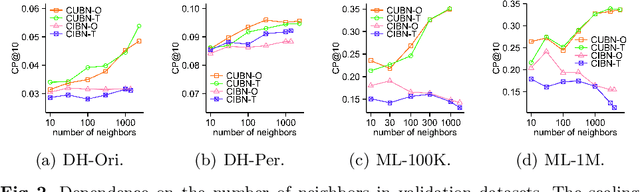
The business objectives of recommenders, such as increasing sales, are aligned with the causal effect of recommendations. Previous recommenders targeting for the causal effect employ the inverse propensity scoring (IPS) in causal inference. However, IPS is prone to suffer from high variance. The matching estimator is another representative method in causal inference field. It does not use propensity and hence free from the above variance problem. In this work, we unify traditional neighborhood recommendation methods with the matching estimator, and develop robust ranking methods for the causal effect of recommendations. Our experiments demonstrate that the proposed methods outperform various baselines in ranking metrics for the causal effect. The results suggest that the proposed methods can achieve more sales and user engagement than previous recommenders.

Approximation Methods for Kernelized Bandits

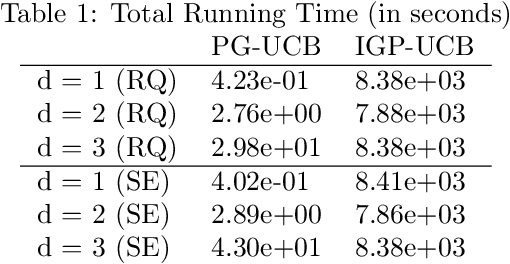
The RKHS bandit problem (also called kernelized multi-armed bandit problem) is an online optimization problem of non-linear functions with noisy feedbacks. Most of the existing methods for the problem have sub-linear regret guarantee at the cost of high computational complexity. For example, IGP-UCB requires at least quadratic time in the number of observed samples at each round. In this paper, using deep results provided by the approximation theory, we approximately reduce the problem to the well-studied linear bandit problem of an appropriate dimension. Then, we propose several algorithms and prove that they achieve comparable regret guarantee to the existing methods (GP-UCB, IGP-UCB) with less computational complexity. Specifically, our proposed methods require polylogarithmic time to select an arm at each round for kernels with "infinite smoothness" (e.g. the rational quadratic and squared exponential kernels). Furthermore, we empirically show our proposed method has comparable regret to the existing method and its running time is much shorter.

Unbiased Learning for the Causal Effect of Recommendation

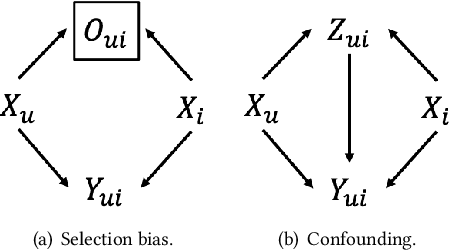
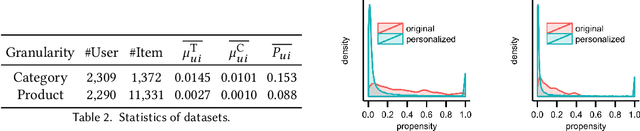
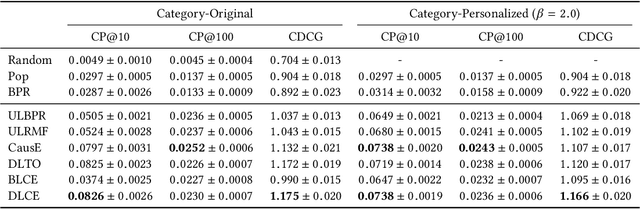
Increasing users' positive interactions, such as purchases or clicks, is an important objective of recommender systems. Recommenders typically aim to select items that users will interact with. If the recommended items are purchased, an increase in sales is expected. However, the items could have been purchased even without recommendation. Thus, we want to recommend items that results in purchases caused by recommendation. This can be formulated as a ranking problem in terms of the causal effect. Despite its importance, this problem has not been well explored in the related research. It is challenging because the ground truth of causal effect is unobservable, and estimating the causal effect is prone to the bias arising from currently deployed recommenders. This paper proposes an unbiased learning framework for the causal effect of recommendation. Based on the inverse propensity scoring technique, the proposed framework first constructs unbiased estimators for ranking metrics. Then, it conducts empirical risk minimization on the estimators with propensity capping, which reduces variance under finite training samples. Based on the framework, we develop an unbiased learning method for the causal effect extension of a ranking metric. We theoretically analyze the unbiasedness of the proposed method and empirically demonstrate that the proposed method outperforms other biased learning methods in various settings.

Submodular Bandit Problem Under Multiple Constraints

The linear submodular bandit problem was proposed to simultaneously address diversified retrieval and online learning in a recommender system. If there is no uncertainty, this problem is equivalent to a submodular maximization problem under a cardinality constraint. However, in some situations, recommendation lists should satisfy additional constraints such as budget constraints, other than a cardinality constraint. Thus, motivated by diversified retrieval considering budget constraints, we introduce a submodular bandit problem under the intersection of $l$ knapsacks and a $k$-system constraint. Here $k$-system constraints form a very general class of constraints including cardinality constraints and the intersection of $k$ matroid constraints. To solve this problem, we propose a non-greedy algorithm that adaptively focuses on a standard or modified upper-confidence bound. We provide a high-probability upper bound of an approximation regret, where the approximation ratio matches that of a fast offline algorithm. Moreover, we perform experiments under various combinations of constraints using a synthetic and two real-world datasets and demonstrate that our proposed methods outperform the existing baselines.