Rethinking Recurrent Neural Networks for Time Series Forecasting: A Reinforced Recurrent Encoder with Prediction-Oriented Proximal Policy Optimization

Time series forecasting plays a crucial role in contemporary engineering information systems for supporting decision-making across various industries, where Recurrent Neural Networks (RNNs) have been widely adopted due to their capability in modeling sequential data. Conventional RNN-based predictors adopt an encoder-only strategy with sliding historical windows as inputs to forecast future values. However, this approach treats all time steps and hidden states equally without considering their distinct contributions to forecasting, leading to suboptimal performance. To address this limitation, we propose a novel Reinforced Recurrent Encoder with Prediction-oriented Proximal Policy Optimization, RRE-PPO4Pred, which significantly improves time series modeling capacity and forecasting accuracy of the RNN models. The core innovations of this method are: (1) A novel Reinforced Recurrent Encoder (RRE) framework that enhances RNNs by formulating their internal adaptation as a Markov Decision Process, creating a unified decision environment capable of learning input feature selection, hidden skip connection, and output target selection; (2) An improved Prediction-oriented Proximal Policy Optimization algorithm, termed PPO4Pred, which is equipped with a Transformer-based agent for temporal reasoning and develops a dynamic transition sampling strategy to enhance sampling efficiency; (3) A co-evolutionary optimization paradigm to facilitate the learning of the RNN predictor and the policy agent, providing adaptive and interactive time series modeling. Comprehensive evaluations on five real-world datasets indicate that our method consistently outperforms existing baselines, and attains accuracy better than state-of-the-art Transformer models, thus providing an advanced time series predictor in engineering informatics.

Close the Gaps: A Learning-while-Doing Algorithm for a Class of Single-Product Revenue Management Problems

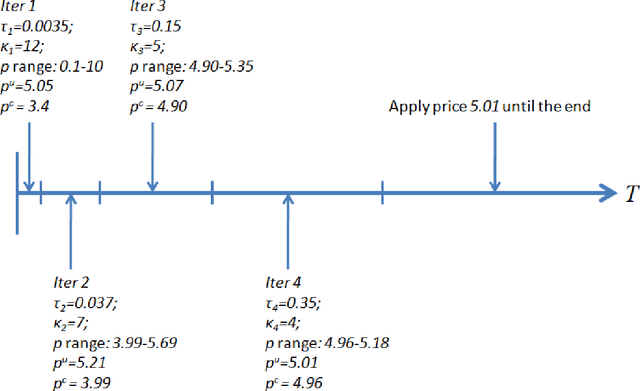
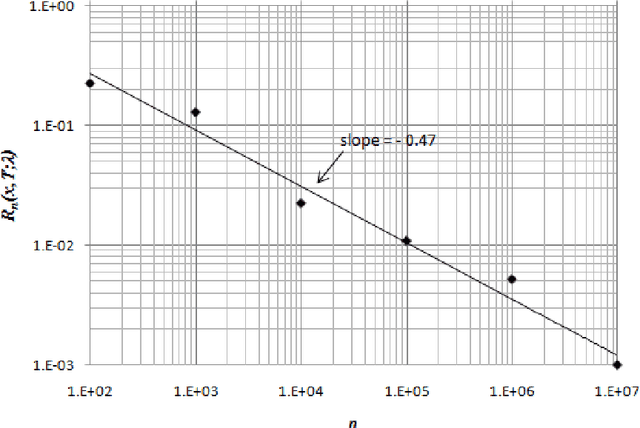
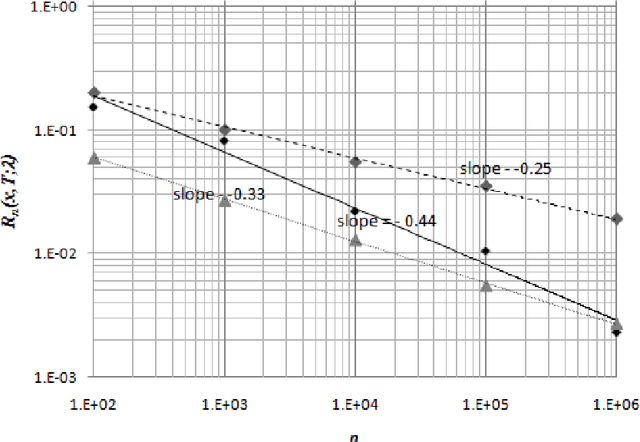
We consider a retailer selling a single product with limited on-hand inventory over a finite selling season. Customer demand arrives according to a Poisson process, the rate of which is influenced by a single action taken by the retailer (such as price adjustment, sales commission, advertisement intensity, etc.). The relationship between the action and the demand rate is not known in advance. However, the retailer is able to learn the optimal action "on the fly" as she maximizes her total expected revenue based on the observed demand reactions. Using the pricing problem as an example, we propose a dynamic "learning-while-doing" algorithm that only involves function value estimation to achieve a near-optimal performance. Our algorithm employs a series of shrinking price intervals and iteratively tests prices within that interval using a set of carefully chosen parameters. We prove that the convergence rate of our algorithm is among the fastest of all possible algorithms in terms of asymptotic "regret" (the relative loss comparing to the full information optimal solution). Our result closes the performance gaps between parametric and non-parametric learning and between a post-price mechanism and a customer-bidding mechanism. Important managerial insight from this research is that the values of information on both the parametric form of the demand function as well as each customer's exact reservation price are less important than prior literature suggests. Our results also suggest that firms would be better off to perform dynamic learning and action concurrently rather than sequentially.