Surrogate modeling of Cellular-Potts Agent-Based Models as a segmentation task using the U-Net neural network architecture

The Cellular-Potts model is a powerful and ubiquitous framework for developing computational models for simulating complex multicellular biological systems. Cellular-Potts models (CPMs) are often computationally expensive due to the explicit modeling of interactions among large numbers of individual model agents and diffusive fields described by partial differential equations (PDEs). In this work, we develop a convolutional neural network (CNN) surrogate model using a U-Net architecture that accounts for periodic boundary conditions. We use this model to accelerate the evaluation of a mechanistic CPM previously used to investigate \textit{in vitro} vasculogenesis. The surrogate model was trained to predict 100 computational steps ahead (Monte-Carlo steps, MCS), accelerating simulation evaluations by a factor of 590 times compared to CPM code execution. Over multiple recursive evaluations, our model effectively captures the emergent behaviors demonstrated by the original Cellular-Potts model of such as vessel sprouting, extension and anastomosis, and contraction of vascular lacunae. This approach demonstrates the potential for deep learning to serve as efficient surrogate models for CPM simulations, enabling faster evaluation of computationally expensive CPM of biological processes at greater spatial and temporal scales.

Combining Machine Learning and Agent-Based Modeling to Study Biomedical Systems

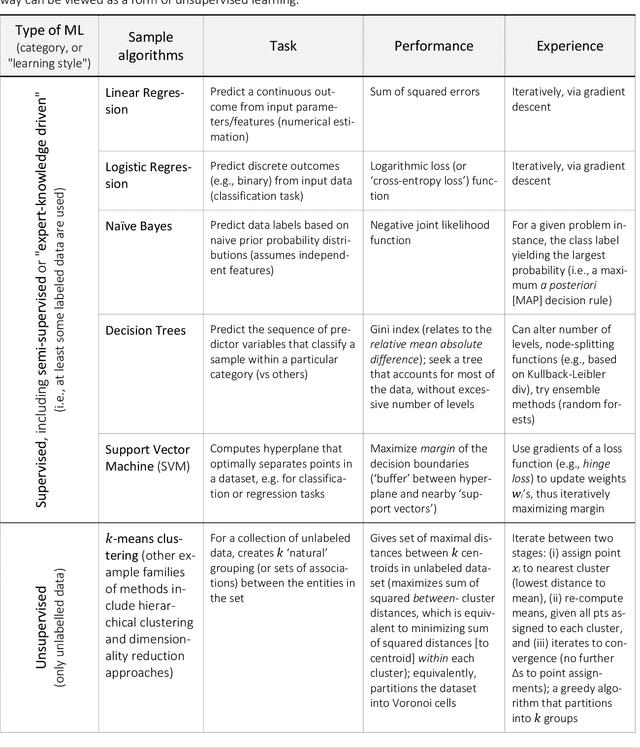
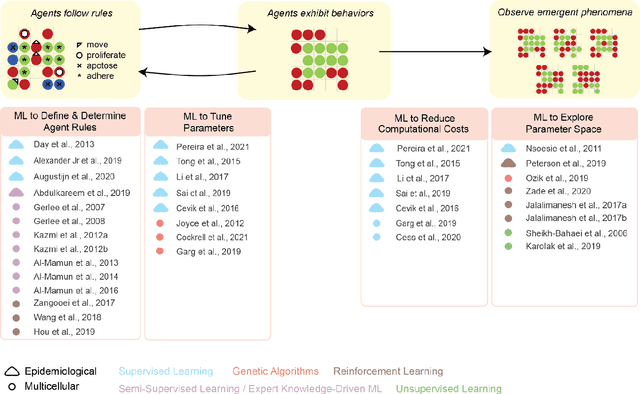
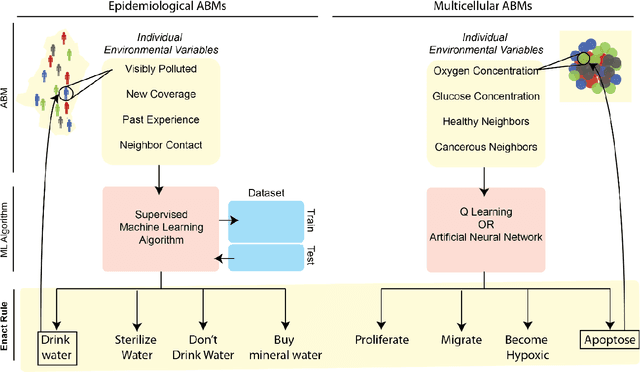
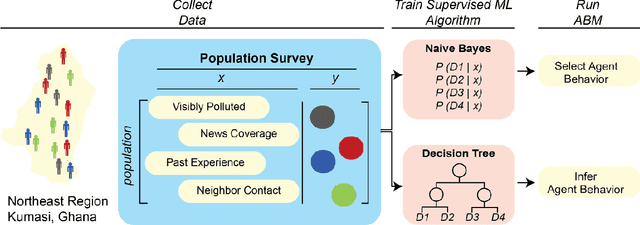
Agent-based modeling (ABM) is a well-established paradigm for simulating complex systems via interactions between constituent entities. Machine learning (ML) refers to approaches whereby statistical algorithms 'learn' from data on their own, without imposing a priori theories of system behavior. Biological systems -- from molecules, to cells, to entire organisms -- consist of vast numbers of entities, governed by complex webs of interactions that span many spatiotemporal scales and exhibit nonlinearity, stochasticity and intricate coupling between entities. The macroscopic properties and collective dynamics of such systems are difficult to capture via continuum modelling and mean-field formalisms. ABM takes a 'bottom-up' approach that obviates these difficulties by enabling one to easily propose and test a set of well-defined 'rules' to be applied to the individual entities (agents) in a system. Evaluating a system and propagating its state over discrete time-steps effectively simulates the system, allowing observables to be computed and system properties to be analyzed. Because the rules that govern an ABM can be difficult to abstract and formulate from experimental data, there is an opportunity to use ML to help infer optimal, system-specific ABM rules. Once such rule-sets are devised, ABM calculations can generate a wealth of data, and ML can be applied there too -- e.g., to probe statistical measures that meaningfully describe a system's stochastic properties. As an example of synergy in the other direction (from ABM to ML), ABM simulations can generate realistic datasets for training ML algorithms (e.g., for regularization, to mitigate overfitting). In these ways, one can envision various synergistic ABM$\rightleftharpoons$ML loops. This review summarizes how ABM and ML have been integrated in contexts that span spatial scales from the cellular to population-level scale epidemiology.