Surrogate modeling of Cellular-Potts Agent-Based Models as a segmentation task using the U-Net neural network architecture

The Cellular-Potts model is a powerful and ubiquitous framework for developing computational models for simulating complex multicellular biological systems. Cellular-Potts models (CPMs) are often computationally expensive due to the explicit modeling of interactions among large numbers of individual model agents and diffusive fields described by partial differential equations (PDEs). In this work, we develop a convolutional neural network (CNN) surrogate model using a U-Net architecture that accounts for periodic boundary conditions. We use this model to accelerate the evaluation of a mechanistic CPM previously used to investigate \textit{in vitro} vasculogenesis. The surrogate model was trained to predict 100 computational steps ahead (Monte-Carlo steps, MCS), accelerating simulation evaluations by a factor of 590 times compared to CPM code execution. Over multiple recursive evaluations, our model effectively captures the emergent behaviors demonstrated by the original Cellular-Potts model of such as vessel sprouting, extension and anastomosis, and contraction of vascular lacunae. This approach demonstrates the potential for deep learning to serve as efficient surrogate models for CPM simulations, enabling faster evaluation of computationally expensive CPM of biological processes at greater spatial and temporal scales.

Deep learning approaches to surrogates for solving the diffusion equation for mechanistic real-world simulations

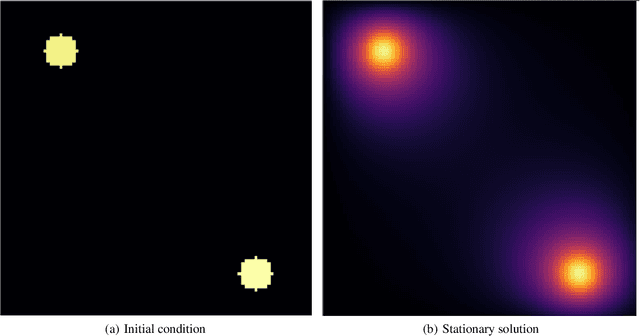
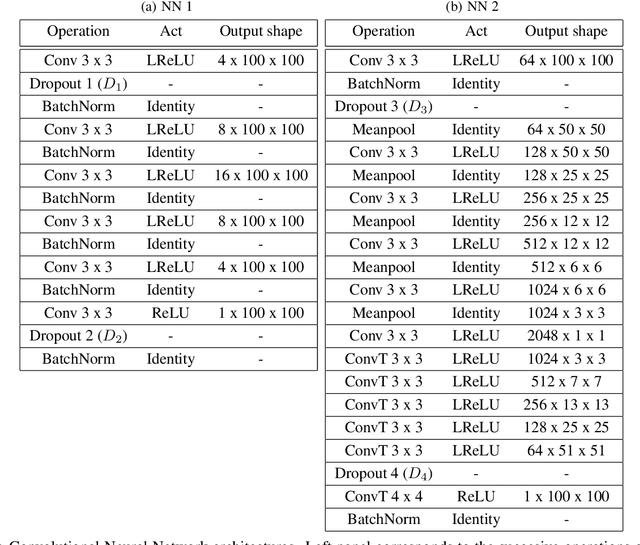
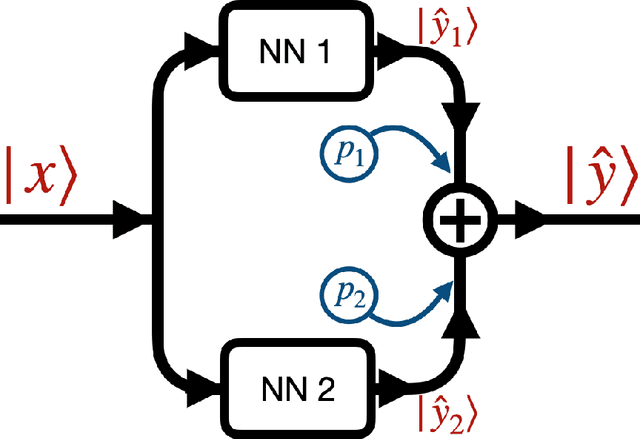
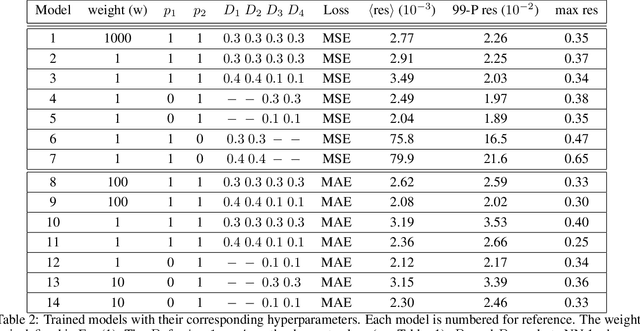
In many mechanistic medical, biological, physical and engineered spatiotemporal dynamic models the numerical solution of partial differential equations (PDEs) can make simulations impractically slow. Biological models require the simultaneous calculation of the spatial variation of concentration of dozens of diffusing chemical species. Machine learning surrogates, neural networks trained to provide approximate solutions to such complicated numerical problems, can often provide speed-ups of several orders of magnitude compared to direct calculation. PDE surrogates enable use of larger models than are possible with direct calculation and can make including such simulations in real-time or near-real time workflows practical. Creating a surrogate requires running the direct calculation tens of thousands of times to generate training data and then training the neural network, both of which are computationally expensive. We use a Convolutional Neural Network to approximate the stationary solution to the diffusion equation in the case of two equal-diameter, circular, constant-value sources located at random positions in a two-dimensional square domain with absorbing boundary conditions. To improve convergence during training, we apply a training approach that uses roll-back to reject stochastic changes to the network that increase the loss function. The trained neural network approximation is about 1e3 times faster than the direct calculation for individual replicas. Because different applications will have different criteria for acceptable approximation accuracy, we discuss a variety of loss functions and accuracy estimators that can help select the best network for a particular application.

Is a good offensive always the best defense?

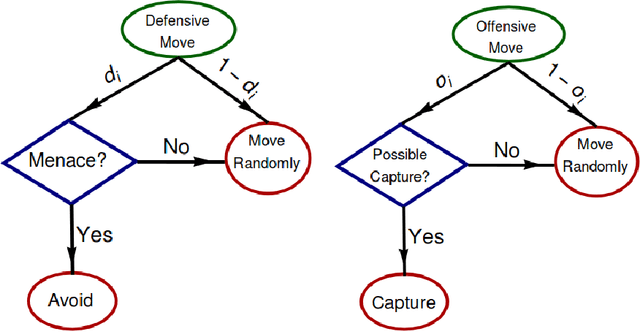
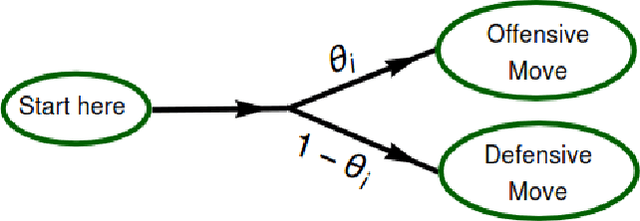
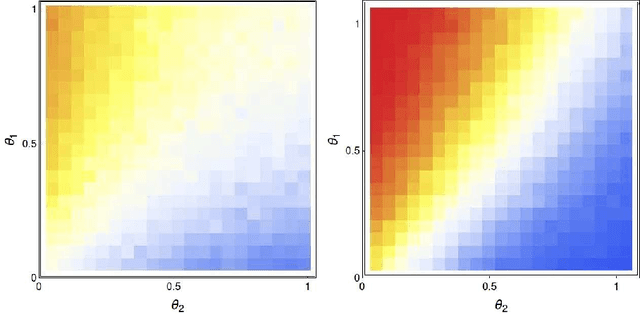
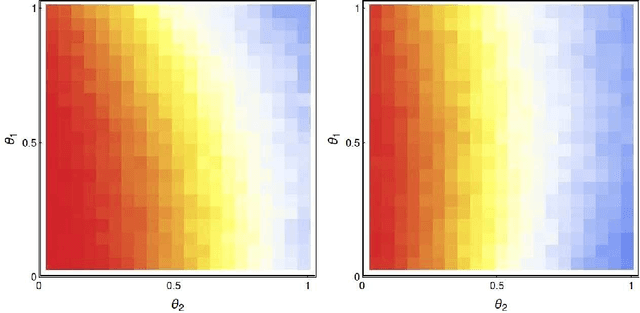
A checkers-like model game with a simplified set of rules is studied through extensive simulations of agents with different expertise and strategies. The introduction of complementary strategies, in a quite general way, provides a tool to mimic the basic ingredients of a wide scope of real games. We find that only for the player having the higher offensive expertise (the dominant player ), maximizing the offensive always increases the probability to win. For the non-dominant player, interestingly, a complete minimization of the offensive becomes the best way to win in many situations, depending on the relative values of the defense expertise. Further simulations on the interplay of defense expertise were done separately, in the context of a fully-offensive scenario, offering a starting point for analytical treatments. In particular, we established that in this scenario the total number of moves is defined only by the player with the lower defensive expertise. We believe that these results stand for a first step towards a new way to improve decisions-making in a large number of zero-sum real games.