An Algorithm for Training Polynomial Networks

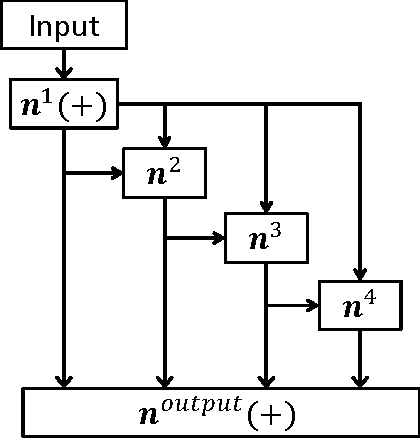
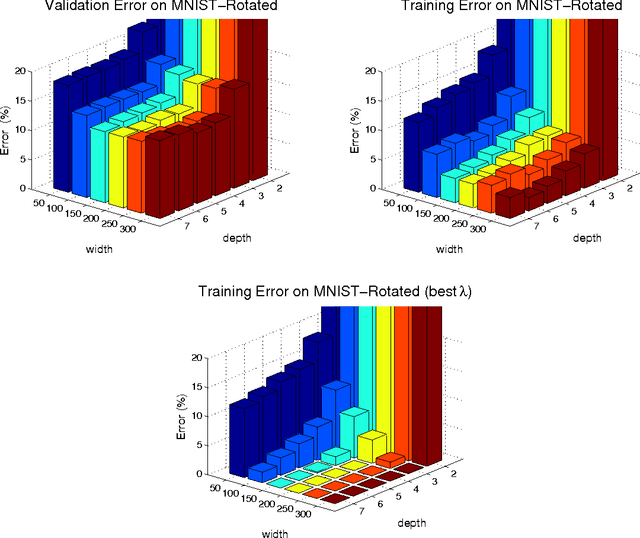
We consider deep neural networks, in which the output of each node is a quadratic function of its inputs. Similar to other deep architectures, these networks can compactly represent any function on a finite training set. The main goal of this paper is the derivation of an efficient layer-by-layer algorithm for training such networks, which we denote as the \emph{Basis Learner}. The algorithm is a universal learner in the sense that the training error is guaranteed to decrease at every iteration, and can eventually reach zero under mild conditions. We present practical implementations of this algorithm, as well as preliminary experimental results. We also compare our deep architecture to other shallow architectures for learning polynomials, in particular kernel learning.

Accelerated Proximal Stochastic Dual Coordinate Ascent for Regularized Loss Minimization

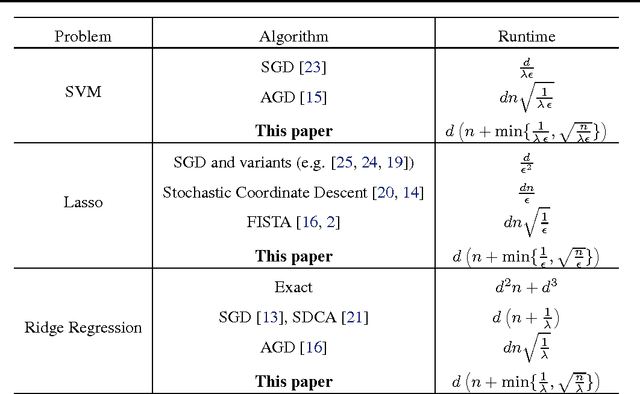
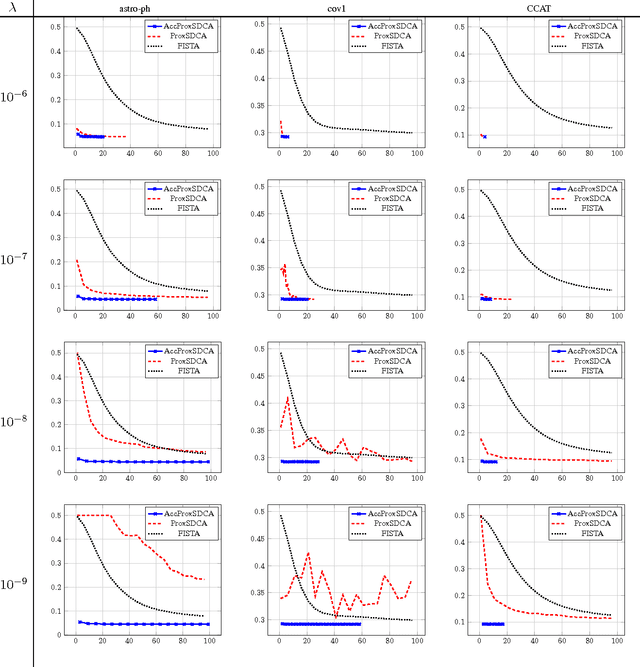
We introduce a proximal version of the stochastic dual coordinate ascent method and show how to accelerate the method using an inner-outer iteration procedure. We analyze the runtime of the framework and obtain rates that improve state-of-the-art results for various key machine learning optimization problems including SVM, logistic regression, ridge regression, Lasso, and multiclass SVM. Experiments validate our theoretical findings.

Efficient Active Learning of Halfspaces: an Aggressive Approach

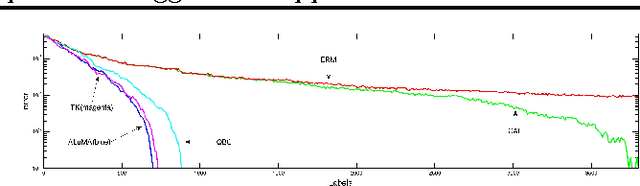
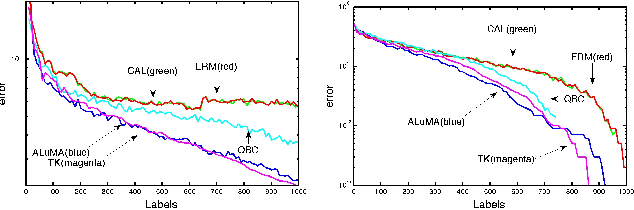
We study pool-based active learning of half-spaces. We revisit the aggressive approach for active learning in the realizable case, and show that it can be made efficient and practical, while also having theoretical guarantees under reasonable assumptions. We further show, both theoretically and experimentally, that it can be preferable to mellow approaches. Our efficient aggressive active learner of half-spaces has formal approximation guarantees that hold when the pool is separable with a margin. While our analysis is focused on the realizable setting, we show that a simple heuristic allows using the same algorithm successfully for pools with low error as well. We further compare the aggressive approach to the mellow approach, and prove that there are cases in which the aggressive approach results in significantly better label complexity compared to the mellow approach. We demonstrate experimentally that substantial improvements in label complexity can be achieved using the aggressive approach, for both realizable and low-error settings.

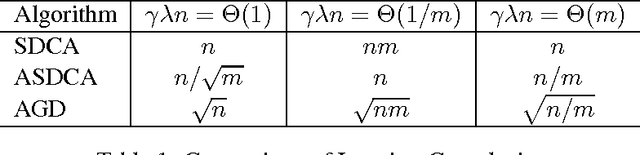
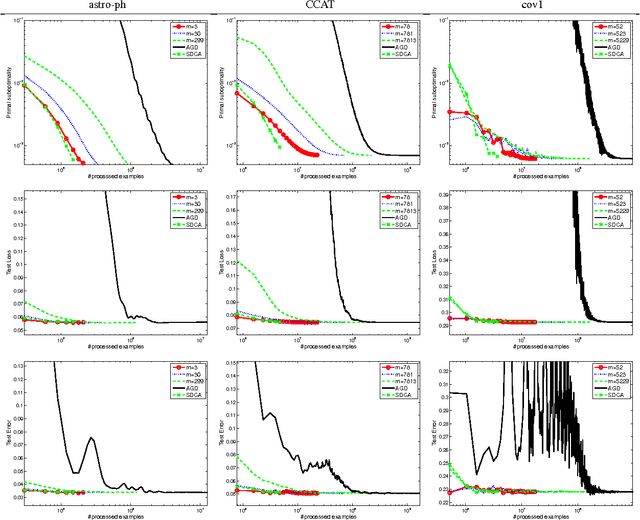
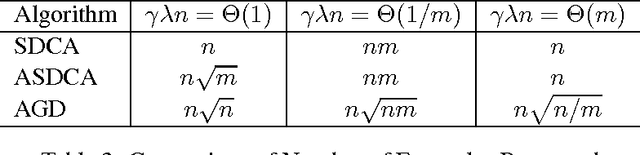
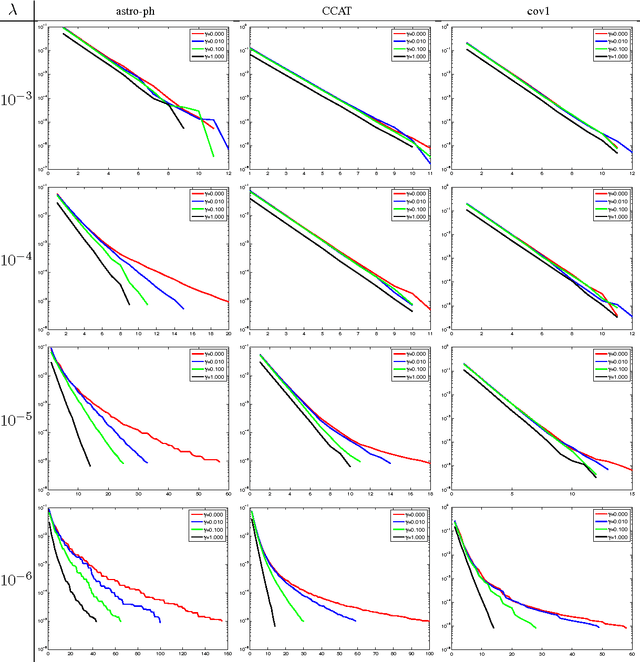
Accelerated Mini-Batch Stochastic Dual Coordinate Ascent

Stochastic dual coordinate ascent (SDCA) is an effective technique for solving regularized loss minimization problems in machine learning. This paper considers an extension of SDCA under the mini-batch setting that is often used in practice. Our main contribution is to introduce an accelerated mini-batch version of SDCA and prove a fast convergence rate for this method. We discuss an implementation of our method over a parallel computing system, and compare the results to both the vanilla stochastic dual coordinate ascent and to the accelerated deterministic gradient descent method of \cite{nesterov2007gradient}.

Stochastic Dual Coordinate Ascent Methods for Regularized Loss Minimization

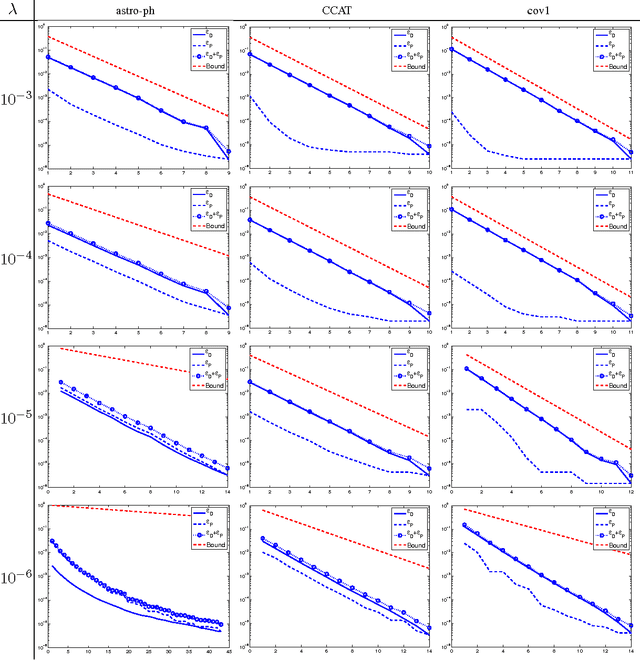
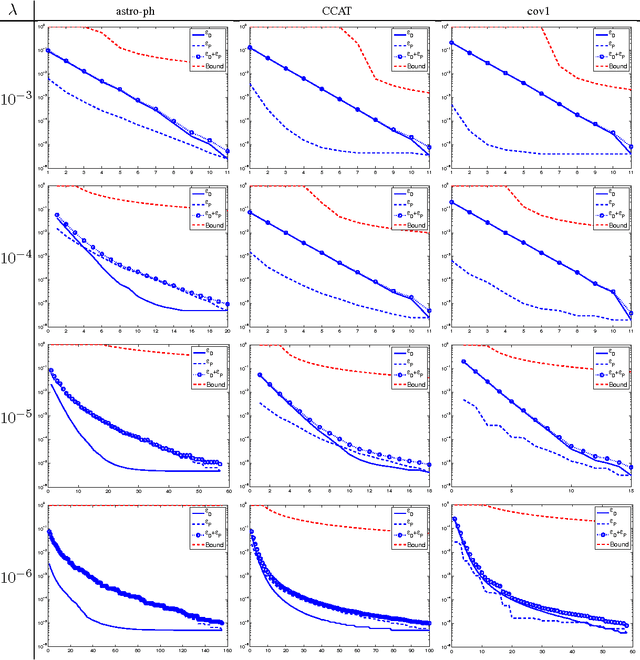
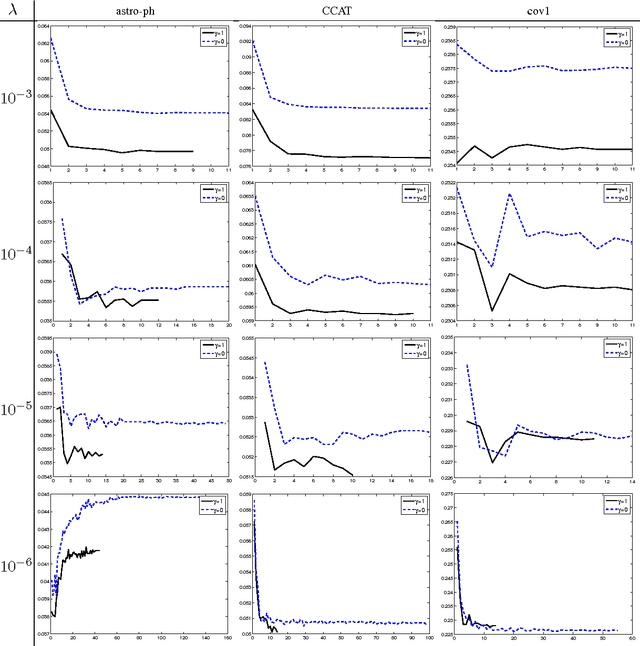
Stochastic Gradient Descent (SGD) has become popular for solving large scale supervised machine learning optimization problems such as SVM, due to their strong theoretical guarantees. While the closely related Dual Coordinate Ascent (DCA) method has been implemented in various software packages, it has so far lacked good convergence analysis. This paper presents a new analysis of Stochastic Dual Coordinate Ascent (SDCA) showing that this class of methods enjoy strong theoretical guarantees that are comparable or better than SGD. This analysis justifies the effectiveness of SDCA for practical applications.

Proximal Stochastic Dual Coordinate Ascent

We introduce a proximal version of dual coordinate ascent method. We demonstrate how the derived algorithmic framework can be used for numerous regularized loss minimization problems, including $\ell_1$ regularization and structured output SVM. The convergence rates we obtain match, and sometimes improve, state-of-the-art results.

The Kernelized Stochastic Batch Perceptron

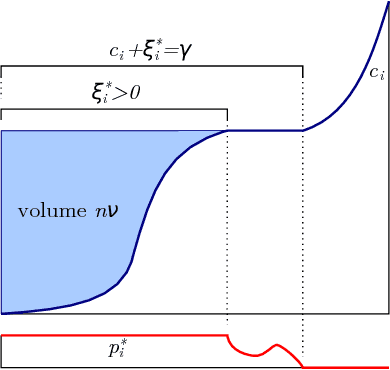
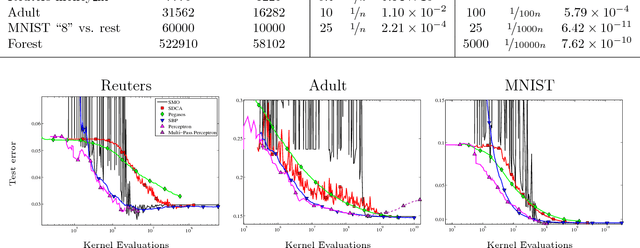
We present a novel approach for training kernel Support Vector Machines, establish learning runtime guarantees for our method that are better then those of any other known kernelized SVM optimization approach, and show that our method works well in practice compared to existing alternatives.

Learning the Experts for Online Sequence Prediction

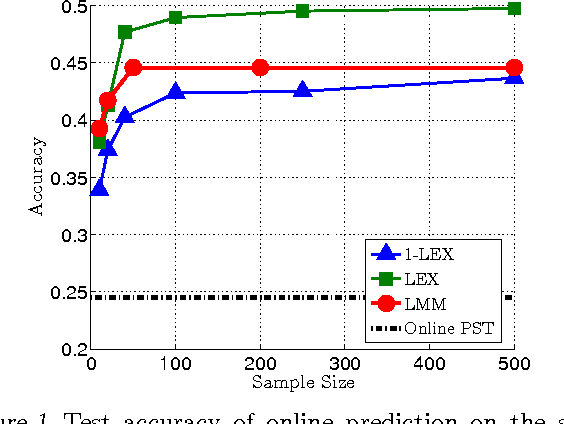
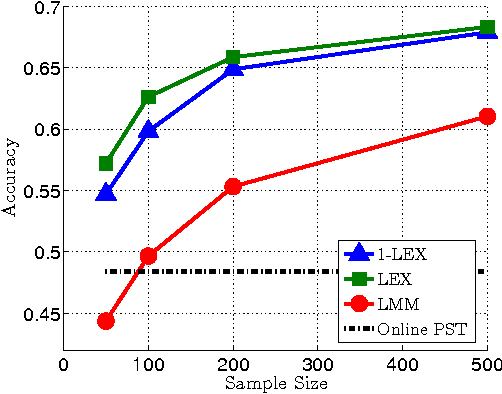
Online sequence prediction is the problem of predicting the next element of a sequence given previous elements. This problem has been extensively studied in the context of individual sequence prediction, where no prior assumptions are made on the origin of the sequence. Individual sequence prediction algorithms work quite well for long sequences, where the algorithm has enough time to learn the temporal structure of the sequence. However, they might give poor predictions for short sequences. A possible remedy is to rely on the general model of prediction with expert advice, where the learner has access to a set of $r$ experts, each of which makes its own predictions on the sequence. It is well known that it is possible to predict almost as well as the best expert if the sequence length is order of $\log(r)$. But, without firm prior knowledge on the problem, it is not clear how to choose a small set of {\em good} experts. In this paper we describe and analyze a new algorithm that learns a good set of experts using a training set of previously observed sequences. We demonstrate the merits of our approach by applying it on the task of click prediction on the web.

Near-Optimal Algorithms for Online Matrix Prediction

In several online prediction problems of recent interest the comparison class is composed of matrices with bounded entries. For example, in the online max-cut problem, the comparison class is matrices which represent cuts of a given graph and in online gambling the comparison class is matrices which represent permutations over n teams. Another important example is online collaborative filtering in which a widely used comparison class is the set of matrices with a small trace norm. In this paper we isolate a property of matrices, which we call (beta,tau)-decomposability, and derive an efficient online learning algorithm, that enjoys a regret bound of O*(sqrt(beta tau T)) for all problems in which the comparison class is composed of (beta,tau)-decomposable matrices. By analyzing the decomposability of cut matrices, triangular matrices, and low trace-norm matrices, we derive near optimal regret bounds for online max-cut, online gambling, and online collaborative filtering. In particular, this resolves (in the affirmative) an open problem posed by Abernethy (2010); Kleinberg et al (2010). Finally, we derive lower bounds for the three problems and show that our upper bounds are optimal up to logarithmic factors. In particular, our lower bound for the online collaborative filtering problem resolves another open problem posed by Shamir and Srebro (2011).

Active Learning of Halfspaces under a Margin Assumption

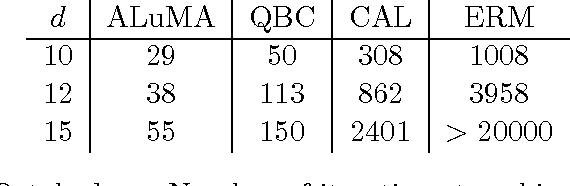
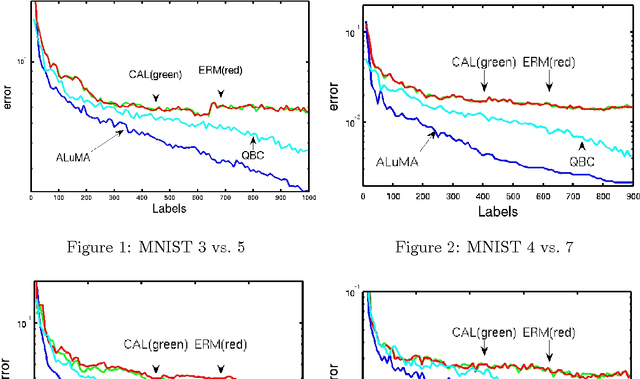
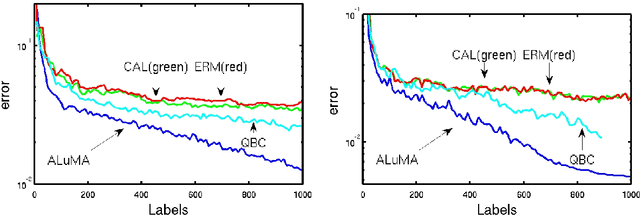
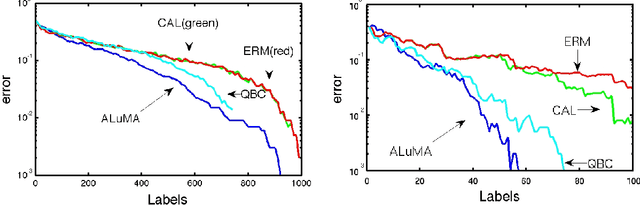
We derive and analyze a new, efficient, pool-based active learning algorithm for halfspaces, called ALuMA. Most previous algorithms show exponential improvement in the label complexity assuming that the distribution over the instance space is close to uniform. This assumption rarely holds in practical applications. Instead, we study the label complexity under a large-margin assumption -- a much more realistic condition, as evident by the success of margin-based algorithms such as SVM. Our algorithm is computationally efficient and comes with formal guarantees on its label complexity. It also naturally extends to the non-separable case and to non-linear kernels. Experiments illustrate the clear advantage of ALuMA over other active learning algorithms.