Hybrid ASP-based Approach to Pattern Mining

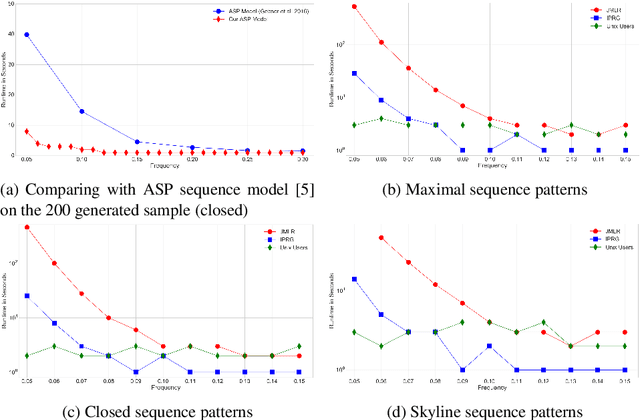
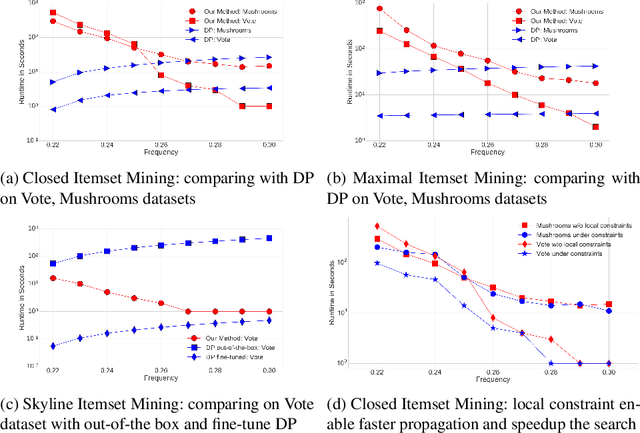
Detecting small sets of relevant patterns from a given dataset is a central challenge in data mining. The relevance of a pattern is based on user-provided criteria; typically, all patterns that satisfy certain criteria are considered relevant. Rule-based languages like Answer Set Programming (ASP) seem well-suited for specifying such criteria in a form of constraints. Although progress has been made, on the one hand, on solving individual mining problems and, on the other hand, developing generic mining systems, the existing methods either focus on scalability or on generality. In this paper we make steps towards combining local (frequency, size, cost) and global (various condensed representations like maximal, closed, skyline) constraints in a generic and efficient way. We present a hybrid approach for itemset, sequence and graph mining which exploits dedicated highly optimized mining systems to detect frequent patterns and then filters the results using declarative ASP. To further demonstrate the generic nature of our hybrid framework we apply it to a problem of approximately tiling a database. Experiments on real-world datasets show the effectiveness of the proposed method and computational gains for itemset, sequence and graph mining, as well as approximate tiling. Under consideration in Theory and Practice of Logic Programming (TPLP).

Sketched Answer Set Programming

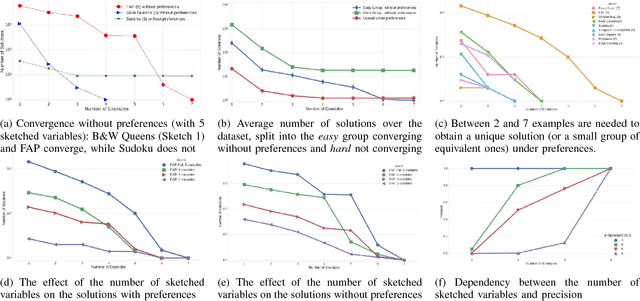
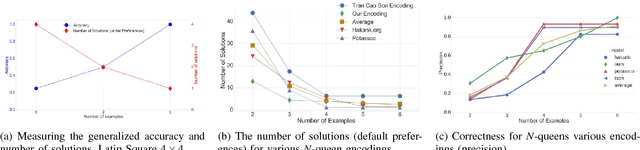
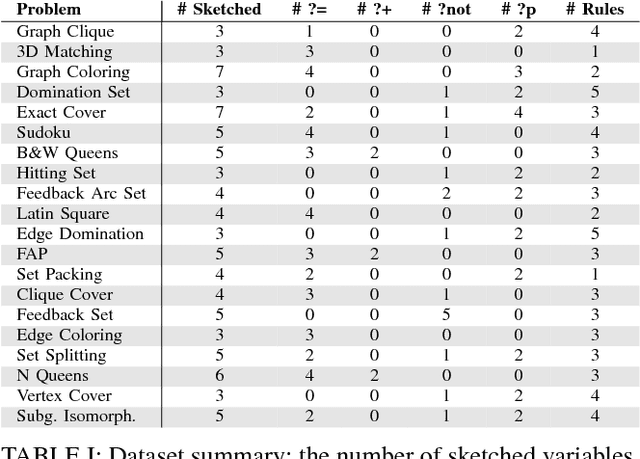
Answer Set Programming (ASP) is a powerful modeling formalism for combinatorial problems. However, writing ASP models is not trivial. We propose a novel method, called Sketched Answer Set Programming (SkASP), aiming at supporting the user in resolving this issue. The user writes an ASP program while marking uncertain parts open with question marks. In addition, the user provides a number of positive and negative examples of the desired program behaviour. The sketched model is rewritten into another ASP program, which is solved by traditional methods. As a result, the user obtains a functional and reusable ASP program modelling her problem. We evaluate our approach on 21 well known puzzles and combinatorial problems inspired by Karp's 21 NP-complete problems and demonstrate a use-case for a database application based on ASP.

Knowledge Representation Analysis of Graph Mining

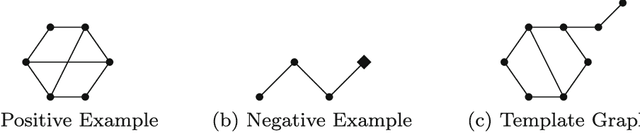
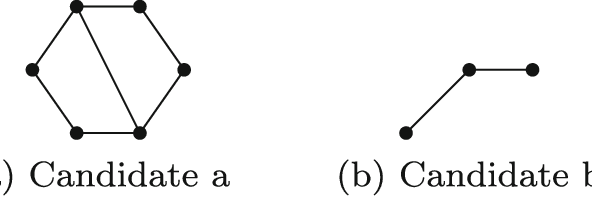
Many problems, especially those with a composite structure, can naturally be expressed in higher order logic. From a KR perspective modeling these problems in an intuitive way is a challenging task. In this paper we study the graph mining problem as an example of a higher order problem. In short, this problem asks us to find a graph that frequently occurs as a subgraph among a set of example graphs. We start from the problem's mathematical definition to solve it in three state-of-the-art specification systems. For IDP and ASP, which have no native support for higher order logic, we propose the use of encoding techniques such as the disjoint union technique and the saturation technique. ProB benefits from the higher order support for sets. We compare the performance of the three approaches to get an idea of the overhead of the higher order support. We propose higher-order language extensions for IDP-like specification languages and discuss what kind of solver support is needed. Native higher order shifts the burden of rewriting specifications using encoding techniques from the user to the solver itself.