Fast Redescription Mining Using Locality-Sensitive Hashing

Redescription mining is a data analysis technique that has found applications in diverse fields. The most used redescription mining approaches involve two phases: finding matching pairs among data attributes and extending the pairs. This process is relatively efficient when the number of attributes remains limited and when the attributes are Boolean, but becomes almost intractable when the data consist of many numerical attributes. In this paper, we present new algorithms that perform the matching and extension orders of magnitude faster than the existing approaches. Our algorithms are based on locality-sensitive hashing with a tailored approach to handle the discretisation of numerical attributes as used in redescription mining.

Visualizing Overlapping Biclusterings and Boolean Matrix Factorizations

Finding (bi-)clusters in bipartite graphs is a popular data analysis approach. Analysts typically want to visualize the clusters, which is simple as long as the clusters are disjoint. However, many modern algorithms find overlapping clusters, making visualization more complicated. In this paper, we study the problem of visualizing \emph{a given clustering} of overlapping clusters in bipartite graphs and the related problem of visualizing Boolean Matrix Factorizations. We conceptualize three different objectives that any good visualization should satisfy: (1) proximity of cluster elements, (2) large consecutive areas of elements from the same cluster, and (3) large uninterrupted areas in the visualization, regardless of the cluster membership. We provide objective functions that capture these goals and algorithms that optimize these objective functions. Interestingly, in experiments on real-world datasets, we find that the best trade-off between these competing goals is achieved by a novel heuristic, which locally aims to place rows and columns with similar cluster membership next to each other.

Finding Rule-Interpretable Non-Negative Data Representation

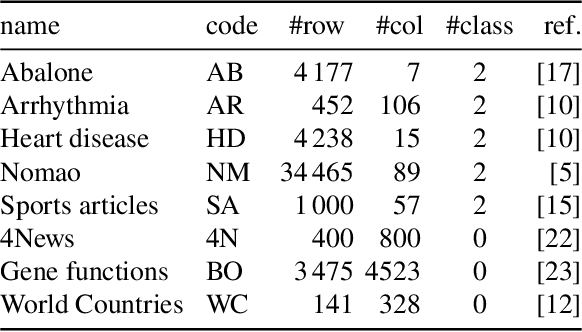
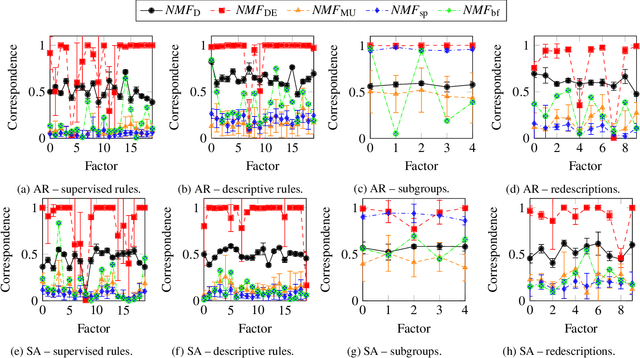
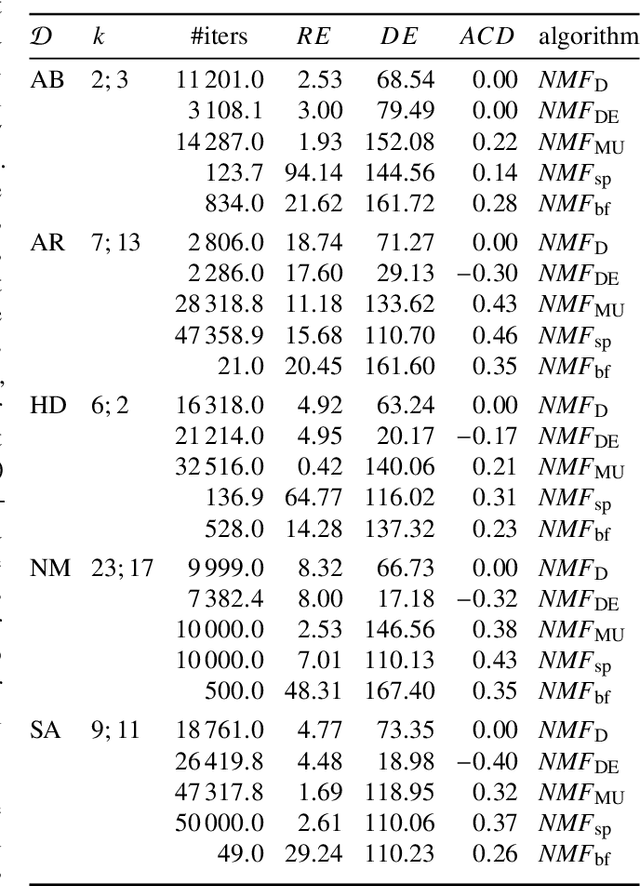
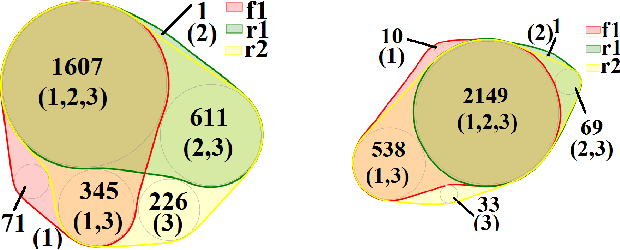
Non-negative Matrix Factorization (NMF) is an intensively used technique for obtaining parts-based, lower dimensional and non-negative representation of non-negative data. It is a popular method in different research fields. Scientists performing research in the fields of biology, medicine and pharmacy often prefer NMF over other dimensionality reduction approaches (such as PCA) because the non-negativity of the approach naturally fits the characteristics of the domain problem and its result is easier to analyze and understand. Despite these advantages, it still can be hard to get exact characterization and interpretation of the NMF's resulting latent factors due to their numerical nature. On the other hand, rule-based approaches are often considered more interpretable but lack the parts-based interpretation. In this work, we present a version of the NMF approach that merges rule-based descriptions with advantages of part-based representation offered by the NMF approach. Given the numerical input data with non-negative entries and a set of rules with high entity coverage, the approach creates the lower-dimensional non-negative representation of the input data in such a way that its factors are described by the appropriate subset of the input rules. In addition to revealing important attributes for latent factors, it allows analyzing relations between these attributes and provides the exact numerical intervals or categorical values they take. The proposed approach provides numerous advantages in tasks such as focused embedding or performing supervised multi-label NMF.

Biclustering and Boolean Matrix Factorization in Data Streams

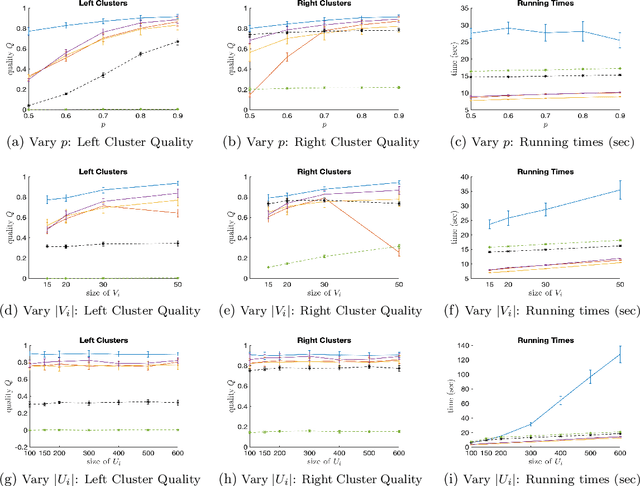
We study the clustering of bipartite graphs and Boolean matrix factorization in data streams. We consider a streaming setting in which the vertices from the left side of the graph arrive one by one together with all of their incident edges. We provide an algorithm that, after one pass over the stream, recovers the set of clusters on the right side of the graph using sublinear space; to the best of our knowledge, this is the first algorithm with this property. We also show that after a second pass over the stream, the left clusters of the bipartite graph can be recovered and we show how to extend our algorithm to solve the Boolean matrix factorization problem (by exploiting the correspondence of Boolean matrices and bipartite graphs). We evaluate an implementation of the algorithm on synthetic data and on real-world data. On real-world datasets the algorithm is orders of magnitudes faster than a static baseline algorithm while providing quality results within a factor 2 of the baseline algorithm. Our algorithm scales linearly in the number of edges in the graph. Finally, we analyze the algorithm theoretically and provide sufficient conditions under which the algorithm recovers a set of planted clusters under a standard random graph model.

Recent Developments in Boolean Matrix Factorization

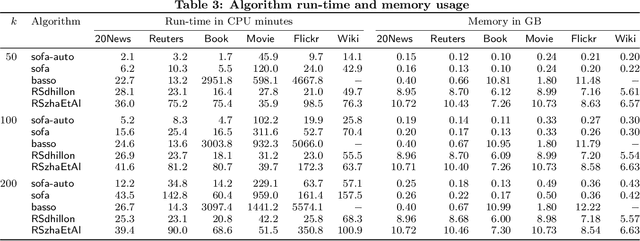
The goal of Boolean Matrix Factorization (BMF) is to approximate a given binary matrix as the product of two low-rank binary factor matrices, where the product of the factor matrices is computed under the Boolean algebra. While the problem is computationally hard, it is also attractive because the binary nature of the factor matrices makes them highly interpretable. In the last decade, BMF has received a considerable amount of attention in the data mining and formal concept analysis communities and, more recently, the machine learning and the theory communities also started studying BMF. In this survey, we give a concise summary of the efforts of all of these communities and raise some open questions which in our opinion require further investigation.

Boolean matrix factorization meets consecutive ones property

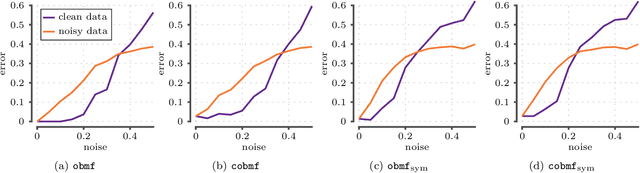
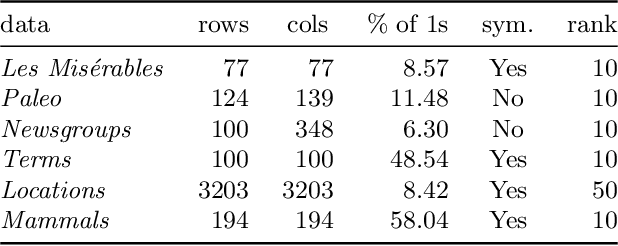
Boolean matrix factorization is a natural and a popular technique for summarizing binary matrices. In this paper, we study a problem of Boolean matrix factorization where we additionally require that the factor matrices have consecutive ones property (OBMF). A major application of this optimization problem comes from graph visualization: standard techniques for visualizing graphs are circular or linear layout, where nodes are ordered in circle or on a line. A common problem with visualizing graphs is clutter due to too many edges. The standard approach to deal with this is to bundle edges together and represent them as ribbon. We also show that we can use OBMF for edge bundling combined with circular or linear layout techniques. We demonstrate that not only this problem is NP-hard but we cannot have a polynomial-time algorithm that yields a multiplicative approximation guarantee (unless P = NP). On the positive side, we develop a greedy algorithm where at each step we look for the best 1-rank factorization. Since even obtaining 1-rank factorization is NP-hard, we propose an iterative algorithm where we fix one side and and find the other, reverse the roles, and repeat. We show that this step can be done in linear time using pq-trees. We also extend the problem to cyclic ones property and symmetric factorizations. Our experiments show that our algorithms find high-quality factorizations and scale well.

Hybrid ASP-based Approach to Pattern Mining

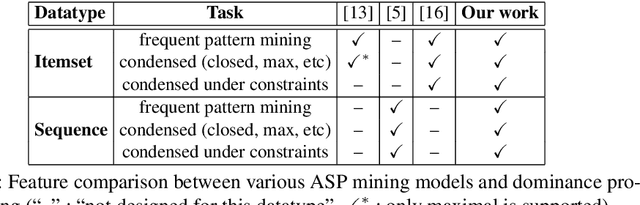
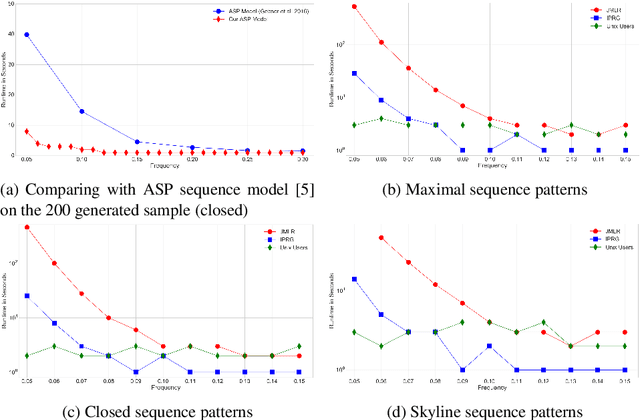
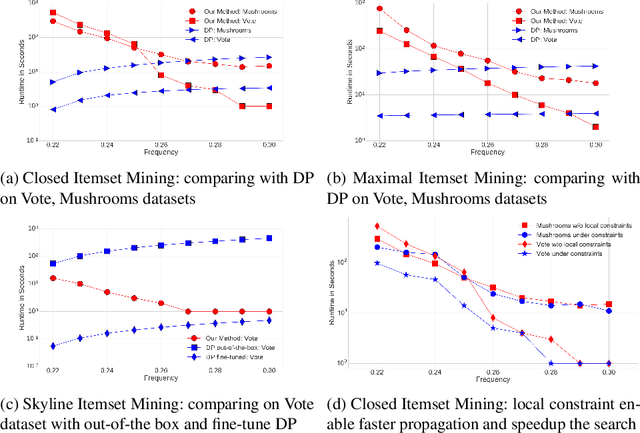
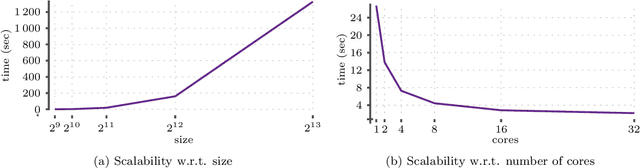
Detecting small sets of relevant patterns from a given dataset is a central challenge in data mining. The relevance of a pattern is based on user-provided criteria; typically, all patterns that satisfy certain criteria are considered relevant. Rule-based languages like Answer Set Programming (ASP) seem well-suited for specifying such criteria in a form of constraints. Although progress has been made, on the one hand, on solving individual mining problems and, on the other hand, developing generic mining systems, the existing methods either focus on scalability or on generality. In this paper we make steps towards combining local (frequency, size, cost) and global (various condensed representations like maximal, closed, skyline) constraints in a generic and efficient way. We present a hybrid approach for itemset, sequence and graph mining which exploits dedicated highly optimized mining systems to detect frequent patterns and then filters the results using declarative ASP. To further demonstrate the generic nature of our hybrid framework we apply it to a problem of approximately tiling a database. Experiments on real-world datasets show the effectiveness of the proposed method and computational gains for itemset, sequence and graph mining, as well as approximate tiling. Under consideration in Theory and Practice of Logic Programming (TPLP).

Latitude: A Model for Mixed Linear-Tropical Matrix Factorization

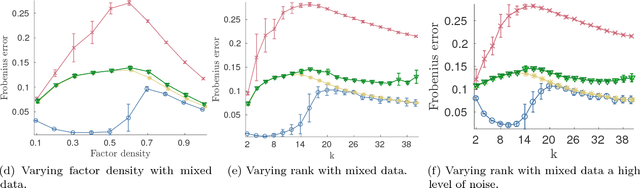
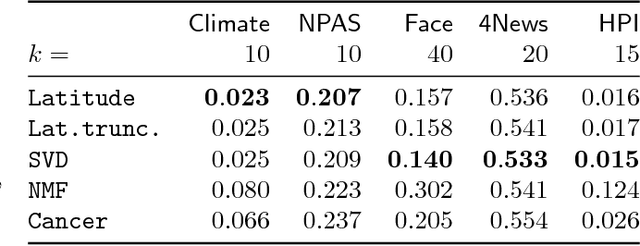
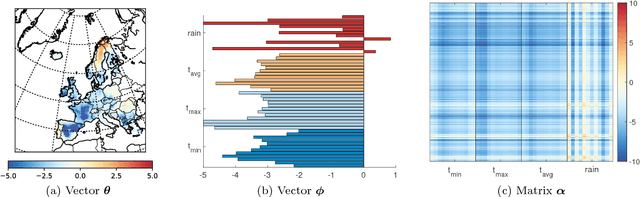
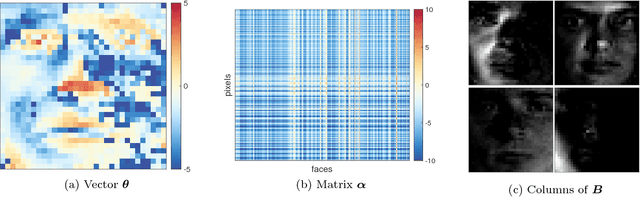
Nonnegative matrix factorization (NMF) is one of the most frequently-used matrix factorization models in data analysis. A significant reason to the popularity of NMF is its interpretability and the `parts of whole' interpretation of its components. Recently, max-times, or subtropical, matrix factorization (SMF) has been introduced as an alternative model with equally interpretable `winner takes it all' interpretation. In this paper we propose a new mixed linear--tropical model, and a new algorithm, called Latitude, that combines NMF and SMF, being able to smoothly alternate between the two. In our model, the data is modeled using the latent factors and latent parameters that control whether the factors are interpreted as NMF or SMF features, or their mixtures. We present an algorithm for our novel matrix factorization. Our experiments show that our algorithm improves over both baselines, and can yield interpretable results that reveal more of the latent structure than either NMF or SMF alone.

Algorithms for Approximate Subtropical Matrix Factorization

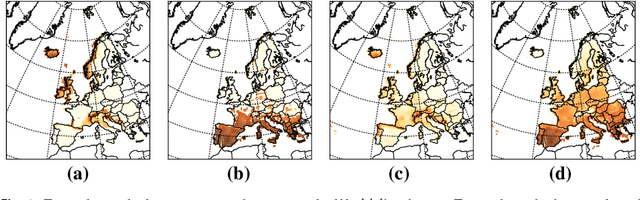
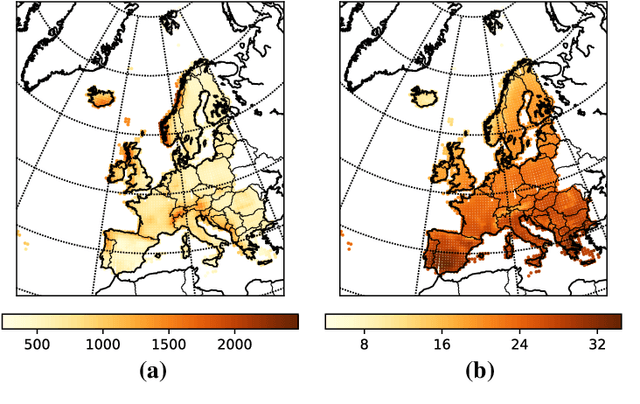
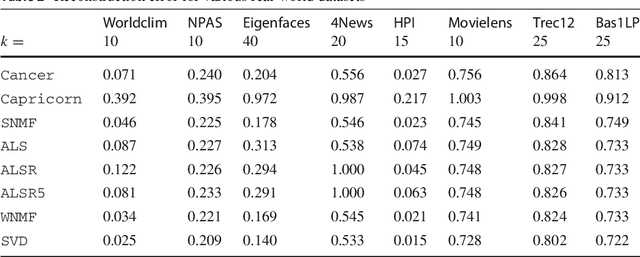
Matrix factorization methods are important tools in data mining and analysis. They can be used for many tasks, ranging from dimensionality reduction to visualization. In this paper we concentrate on the use of matrix factorizations for finding patterns from the data. Rather than using the standard algebra -- and the summation of the rank-1 components to build the approximation of the original matrix -- we use the subtropical algebra, which is an algebra over the nonnegative real values with the summation replaced by the maximum operator. Subtropical matrix factorizations allow "winner-takes-it-all" interpretations of the rank-1 components, revealing different structure than the normal (nonnegative) factorizations. We study the complexity and sparsity of the factorizations, and present a framework for finding low-rank subtropical factorizations. We present two specific algorithms, called Capricorn and Cancer, that are part of our framework. They can be used with data that has been corrupted with different types of noise, and with different error metrics, including the sum-of-absolute differences, Frobenius norm, and Jensen--Shannon divergence. Our experiments show that the algorithms perform well on data that has subtropical structure, and that they can find factorizations that are both sparse and easy to interpret.