Practical Multi-fidelity Bayesian Optimization for Hyperparameter Tuning

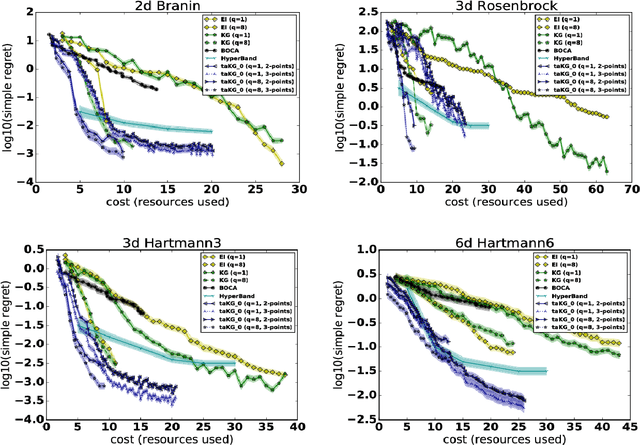
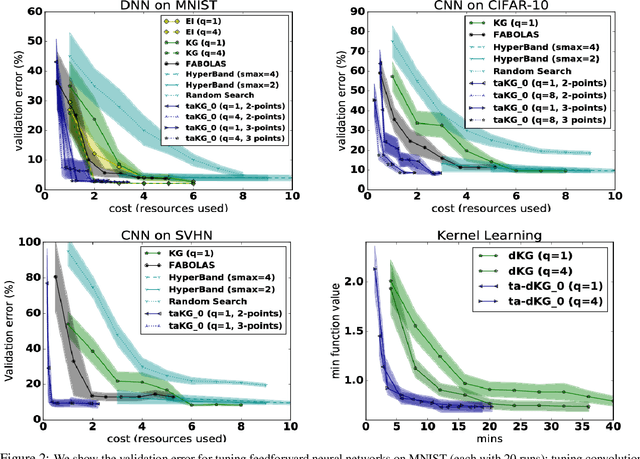
Bayesian optimization is popular for optimizing time-consuming black-box objectives. Nonetheless, for hyperparameter tuning in deep neural networks, the time required to evaluate the validation error for even a few hyperparameter settings remains a bottleneck. Multi-fidelity optimization promises relief using cheaper proxies to such objectives --- for example, validation error for a network trained using a subset of the training points or fewer iterations than required for convergence. We propose a highly flexible and practical approach to multi-fidelity Bayesian optimization, focused on efficiently optimizing hyperparameters for iteratively trained supervised learning models. We introduce a new acquisition function, the trace-aware knowledge-gradient, which efficiently leverages both multiple continuous fidelity controls and trace observations --- values of the objective at a sequence of fidelities, available when varying fidelity using training iterations. We provide a provably convergent method for optimizing our acquisition function and show it outperforms state-of-the-art alternatives for hyperparameter tuning of deep neural networks and large-scale kernel learning.

Bayesian Optimization with Expensive Integrands

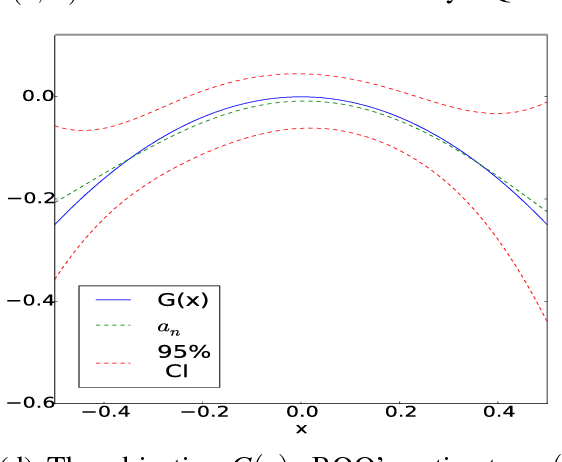
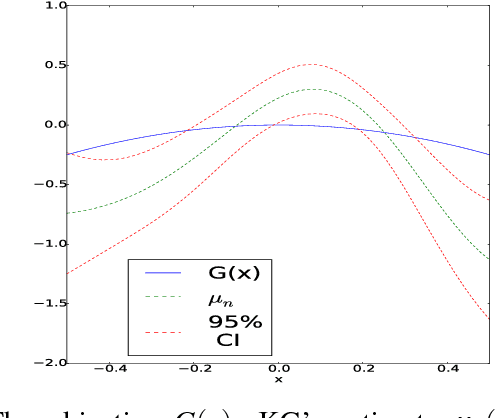
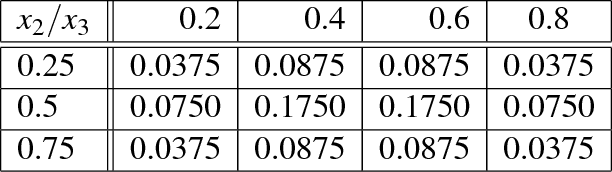
We propose a Bayesian optimization algorithm for objective functions that are sums or integrals of expensive-to-evaluate functions, allowing noisy evaluations. These objective functions arise in multi-task Bayesian optimization for tuning machine learning hyperparameters, optimization via simulation, and sequential design of experiments with random environmental conditions. Our method is average-case optimal by construction when a single evaluation of the integrand remains within our evaluation budget. Achieving this one-step optimality requires solving a challenging value of information optimization problem, for which we provide a novel efficient discretization-free computational method. We also provide consistency proofs for our method in both continuum and discrete finite domains for objective functions that are sums. In numerical experiments comparing against previous state-of-the-art methods, including those that also leverage sum or integral structure, our method performs as well or better across a wide range of problems and offers significant improvements when evaluations are noisy or the integrand varies smoothly in the integrated variables.

Stratified Bayesian Optimization

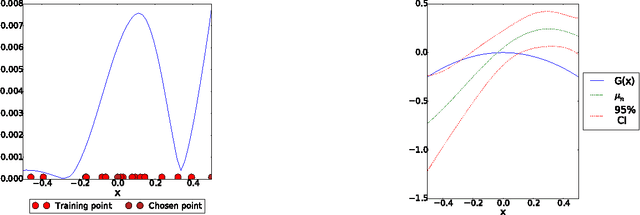
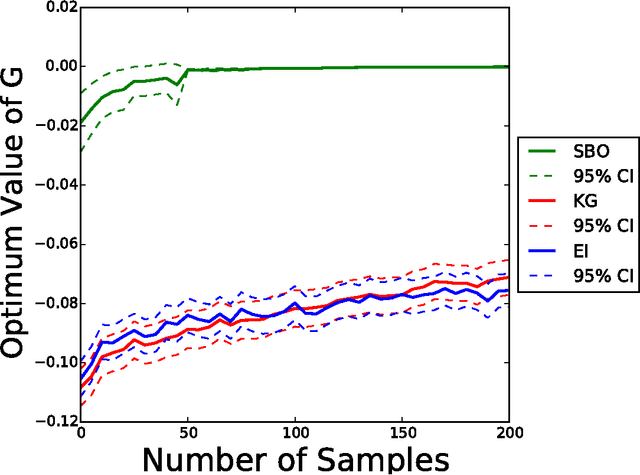
We consider derivative-free black-box global optimization of expensive noisy functions, when most of the randomness in the objective is produced by a few influential scalar random inputs. We present a new Bayesian global optimization algorithm, called Stratified Bayesian Optimization (SBO), which uses this strong dependence to improve performance. Our algorithm is similar in spirit to stratification, a technique from simulation, which uses strong dependence on a categorical representation of the random input to reduce variance. We demonstrate in numerical experiments that SBO outperforms state-of-the-art Bayesian optimization benchmarks that do not leverage this dependence.