Santanu S. Dey
Variable Selection for Kernel Two-Sample Tests
Feb 15, 2023Abstract:We consider the variable selection problem for two-sample tests, aiming to select the most informative features to best distinguish samples from two groups. We propose a kernel maximum mean discrepancy (MMD) framework to solve this problem and further derive its equivalent mixed-integer programming formulations for linear, quadratic, and Gaussian types of kernel functions. Our proposed framework admits advantages of both computational efficiency and nice statistical properties: (i) A closed-form solution is provided for the linear kernel case. Despite NP-hardness, we provide an exact mixed-integer semi-definite programming formulation for the quadratic kernel case, which further motivates the development of exact and approximation algorithms. We propose a convex-concave procedure that finds critical points for the Gaussian kernel case. (ii) We provide non-asymptotic uncertainty quantification of our proposed formulation under null and alternative scenarios. Experimental results demonstrate good performance of our framework.
Complexity of Training ReLU Neural Network
Sep 27, 2018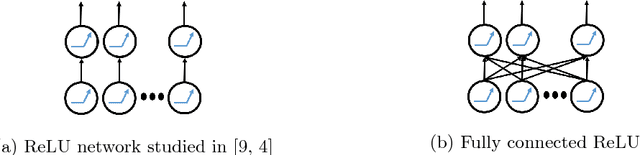
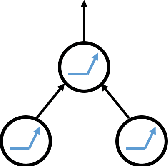
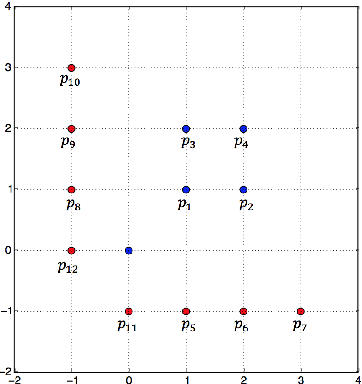
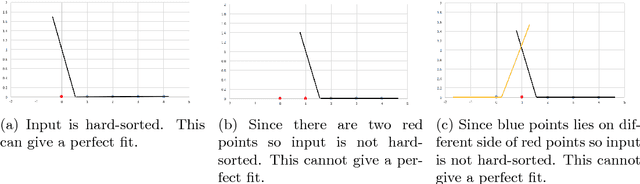
Abstract:In this paper, we explore some basic questions on the complexity of training Neural networks with ReLU activation function. We show that it is NP-hard to train a two- hidden layer feedforward ReLU neural network. If dimension d of the data is fixed then we show that there exists a polynomial time algorithm for the same training problem. We also show that if sufficient over-parameterization is provided in the first hidden layer of ReLU neural network then there is a polynomial time algorithm which finds weights such that output of the over-parameterized ReLU neural network matches with the output of the given data
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge