Quantum Approaches to Urban Logistics: From Core QAOA to Clustered Scalability

The Traveling Salesman Problem (TSP) is a fundamental challenge in combinatorial optimization, widely applied in logistics and transportation. As the size of TSP instances grows, traditional algorithms often struggle to produce high-quality solutions within reasonable timeframes. This study investigates the potential of the Quantum Approximate Optimization Algorithm (QAOA), a hybrid quantum-classical method, to solve TSP under realistic constraints. We adopt a QUBO-based formulation of TSP that integrates real-world logistical constraints reflecting operational conditions, such as vehicle capacity, road accessibility, and time windows, while ensuring compatibility with the limitations of current quantum hardware. Our experiments are conducted in a simulated environment using high-performance computing (HPC) resources to assess QAOA's performance across different problem sizes and quantum circuit depths. In order to improve scalability, we propose clustering QAOA (Cl-QAOA), a hybrid approach combining classical machine learning with QAOA. This method decomposes large TSP instances into smaller sub-problems, making quantum optimization feasible even on devices with a limited number of qubits. The results offer a comprehensive evaluation of QAOA's strengths and limitations in solving constrained TSP scenarios. This study advances quantum optimization and lays groundwork for future large-scale applications.

Training very large scale nonlinear SVMs using Alternating Direction Method of Multipliers coupled with the Hierarchically Semi-Separable kernel approximations

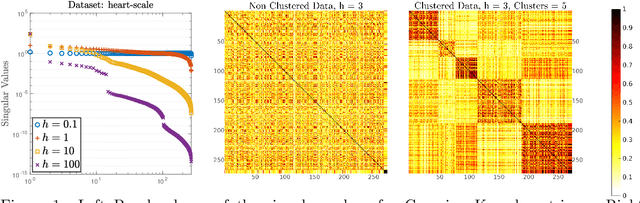
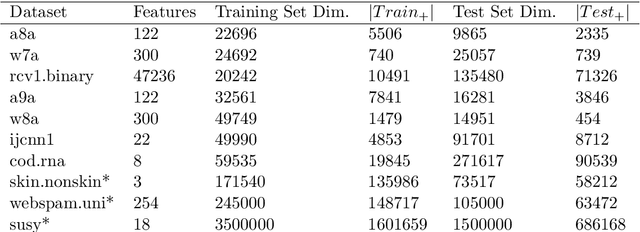
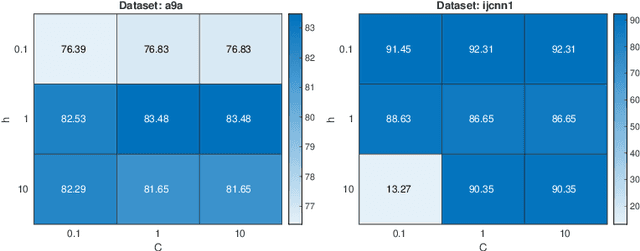
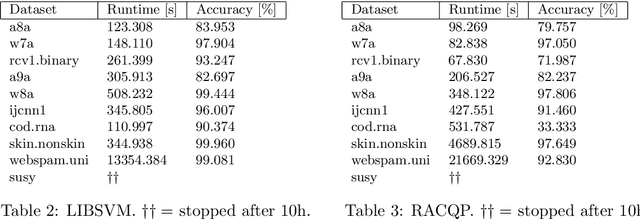
Typically, nonlinear Support Vector Machines (SVMs) produce significantly higher classification quality when compared to linear ones but, at the same time, their computational complexity is prohibitive for large-scale datasets: this drawback is essentially related to the necessity to store and manipulate large, dense and unstructured kernel matrices. Despite the fact that at the core of training a SVM there is a \textit{simple} convex optimization problem, the presence of kernel matrices is responsible for dramatic performance reduction, making SVMs unworkably slow for large problems. Aiming to an efficient solution of large-scale nonlinear SVM problems, we propose the use of the \textit{Alternating Direction Method of Multipliers} coupled with \textit{Hierarchically Semi-Separable} (HSS) kernel approximations. As shown in this work, the detailed analysis of the interaction among their algorithmic components unveils a particularly efficient framework and indeed, the presented experimental results demonstrate a significant speed-up when compared to the \textit{state-of-the-art} nonlinear SVM libraries (without significantly affecting the classification accuracy).