How Global Calibration Strengthens Multiaccuracy

Multiaccuracy and multicalibration are multigroup fairness notions for prediction that have found numerous applications in learning and computational complexity. They can be achieved from a single learning primitive: weak agnostic learning. Here we investigate the power of multiaccuracy as a learning primitive, both with and without the additional assumption of calibration. We find that multiaccuracy in itself is rather weak, but that the addition of global calibration (this notion is called calibrated multiaccuracy) boosts its power substantially, enough to recover implications that were previously known only assuming the stronger notion of multicalibration. We give evidence that multiaccuracy might not be as powerful as standard weak agnostic learning, by showing that there is no way to post-process a multiaccurate predictor to get a weak learner, even assuming the best hypothesis has correlation $1/2$. Rather, we show that it yields a restricted form of weak agnostic learning, which requires some concept in the class to have correlation greater than $1/2$ with the labels. However, by also requiring the predictor to be calibrated, we recover not just weak, but strong agnostic learning. A similar picture emerges when we consider the derivation of hardcore measures from predictors satisfying multigroup fairness notions. On the one hand, while multiaccuracy only yields hardcore measures of density half the optimal, we show that (a weighted version of) calibrated multiaccuracy achieves optimal density. Our results yield new insights into the complementary roles played by multiaccuracy and calibration in each setting. They shed light on why multiaccuracy and global calibration, although not particularly powerful by themselves, together yield considerably stronger notions.

Reconciling Predictive Multiplicity in Practice

Many machine learning applications predict individual probabilities, such as the likelihood that a person develops a particular illness. Since these probabilities are unknown, a key question is how to address situations in which different models trained on the same dataset produce varying predictions for certain individuals. This issue is exemplified by the model multiplicity (MM) phenomenon, where a set of comparable models yield inconsistent predictions. Roth, Tolbert, and Weinstein recently introduced a reconciliation procedure, the Reconcile algorithm, to address this problem. Given two disagreeing models, the algorithm leverages their disagreement to falsify and improve at least one of the models. In this paper, we empirically analyze the Reconcile algorithm using five widely-used fairness datasets: COMPAS, Communities and Crime, Adult, Statlog (German Credit Data), and the ACS Dataset. We examine how Reconcile fits within the model multiplicity literature and compare it to existing MM solutions, demonstrating its effectiveness. We also discuss potential improvements to the Reconcile algorithm theoretically and practically. Finally, we extend the Reconcile algorithm to the setting of causal inference, given that different competing estimators can again disagree on specific causal average treatment effect (CATE) values. We present the first extension of the Reconcile algorithm in causal inference, analyze its theoretical properties, and conduct empirical tests. Our results confirm the practical effectiveness of Reconcile and its applicability across various domains.

PCACE: A Statistical Approach to Ranking Neurons for CNN Interpretability

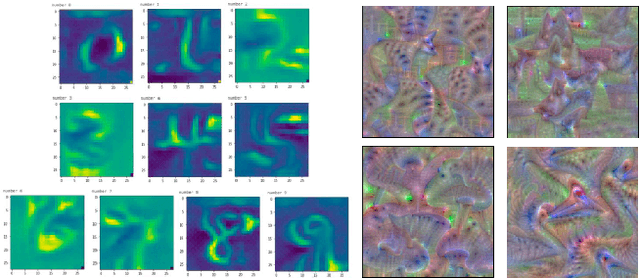
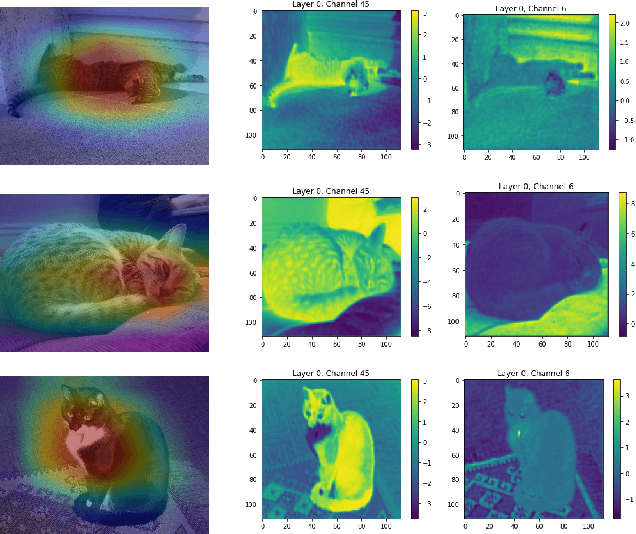
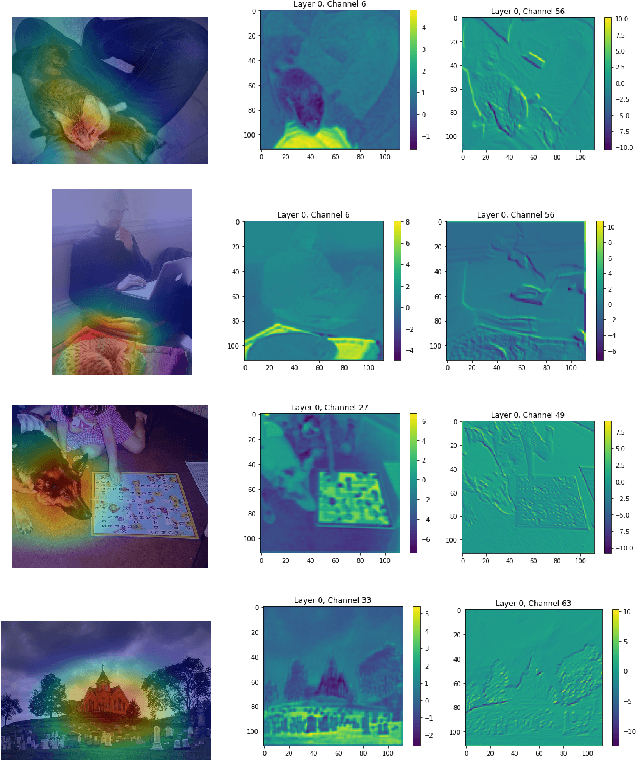
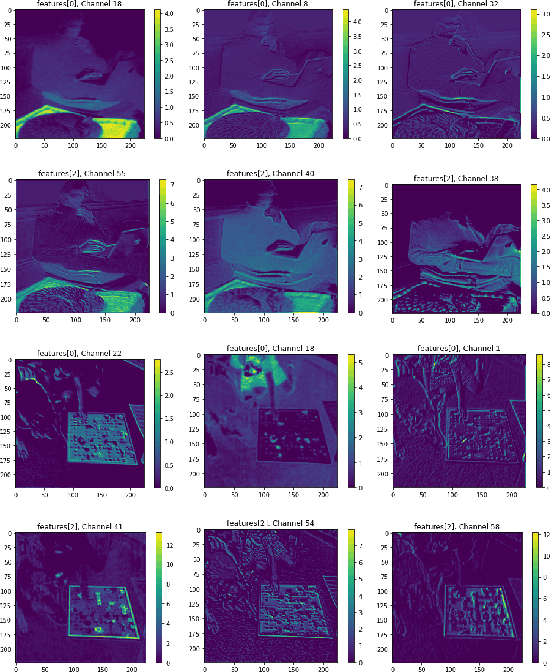
In this paper we introduce a new problem within the growing literature of interpretability for convolution neural networks (CNNs). While previous work has focused on the question of how to visually interpret CNNs, we ask what it is that we care to interpret, that is, which layers and neurons are worth our attention? Due to the vast size of modern deep learning network architectures, automated, quantitative methods are needed to rank the relative importance of neurons so as to provide an answer to this question. We present a new statistical method for ranking the hidden neurons in any convolutional layer of a network. We define importance as the maximal correlation between the activation maps and the class score. We provide different ways in which this method can be used for visualization purposes with MNIST and ImageNet, and show a real-world application of our method to air pollution prediction with street-level images.

Evaluating Word Embeddings with Categorical Modularity

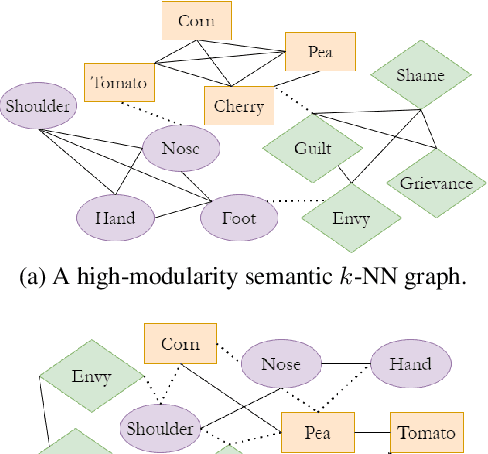
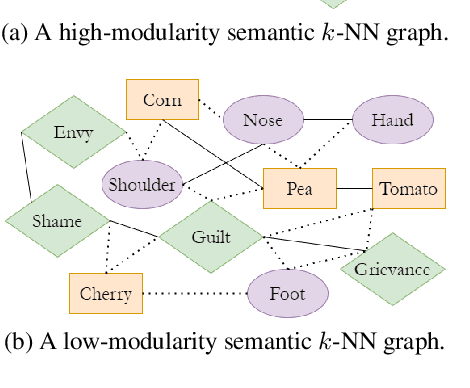
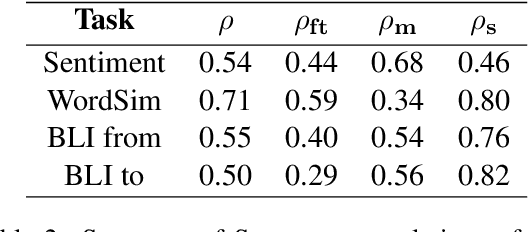
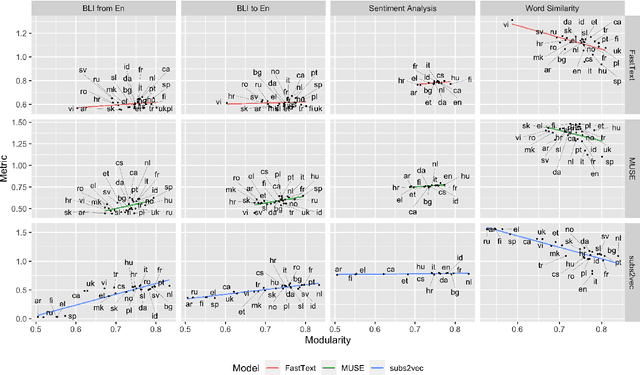
We introduce categorical modularity, a novel low-resource intrinsic metric to evaluate word embedding quality. Categorical modularity is a graph modularity metric based on the $k$-nearest neighbor graph constructed with embedding vectors of words from a fixed set of semantic categories, in which the goal is to measure the proportion of words that have nearest neighbors within the same categories. We use a core set of 500 words belonging to 59 neurobiologically motivated semantic categories in 29 languages and analyze three word embedding models per language (FastText, MUSE, and subs2vec). We find moderate to strong positive correlations between categorical modularity and performance on the monolingual tasks of sentiment analysis and word similarity calculation and on the cross-lingual task of bilingual lexicon induction both to and from English. Overall, we suggest that categorical modularity provides non-trivial predictive information about downstream task performance, with breakdowns of correlations by model suggesting some meta-predictive properties about semantic information loss as well.