Robustly Invertible Nonlinear Dynamics and the BiLipREN: Contracting Neural Models with Contracting Inverses

We study the invertibility of nonlinear dynamical systems from the perspective of contraction and incremental stability analysis and propose a new invertible recurrent neural model: the BiLipREN. In particular, we consider a nonlinear state space model to be robustly invertible if an inverse exists with a state space realisation, and both the forward model and its inverse are contracting, i.e. incrementally exponentially stable, and Lipschitz, i.e. have bounded incremental gain. This property of bi-Lipschitzness implies both robustness in the sense of sensitivity to input perturbations, as well as robust distinguishability of different inputs from their corresponding outputs, i.e. the inverse model robustly reconstructs the input sequence despite small perturbations to the initial conditions and measured output. Building on this foundation, we propose a parameterization of neural dynamic models: bi-Lipschitz recurrent equilibrium networks (biLipREN), which are robustly invertible by construction. Moreover, biLipRENs can be composed with orthogonal linear systems to construct more general bi-Lipschitz dynamic models, e.g., a nonlinear analogue of minimum-phase/all-pass (inner/outer) factorization. We illustrate the utility of our proposed approach with numerical examples.

Negative Imaginary Neural ODEs: Learning to Control Mechanical Systems with Stability Guarantees

We propose a neural control method to provide guaranteed stabilization for mechanical systems using a novel negative imaginary neural ordinary differential equation (NINODE) controller. Specifically, we employ neural networks with desired properties as state-space function matrices within a Hamiltonian framework to ensure the system possesses the NI property. This NINODE system can serve as a controller that asymptotically stabilizes an NI plant under certain conditions. For mechanical plants with colocated force actuators and position sensors, we demonstrate that all the conditions required for stability can be translated into regularity constraints on the neural networks used in the controller. We illustrate the utility, effectiveness, and stability guarantees of the NINODE controller through an example involving a nonlinear mass-spring system.

R2DN: Scalable Parameterization of Contracting and Lipschitz Recurrent Deep Networks

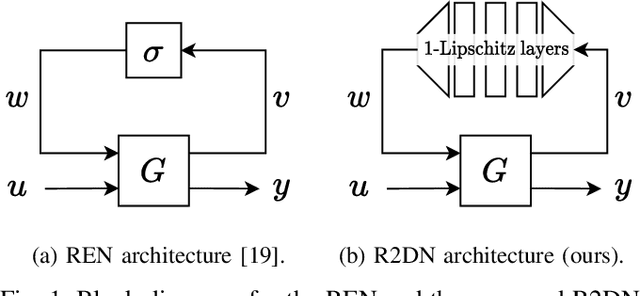
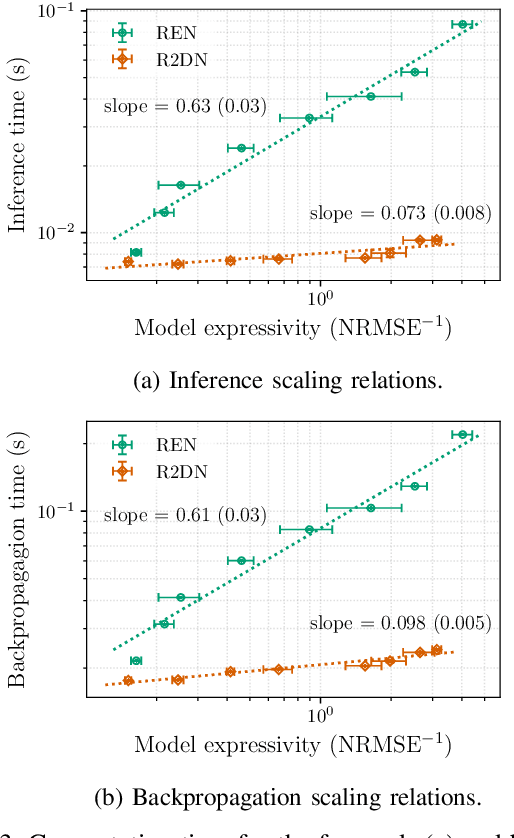
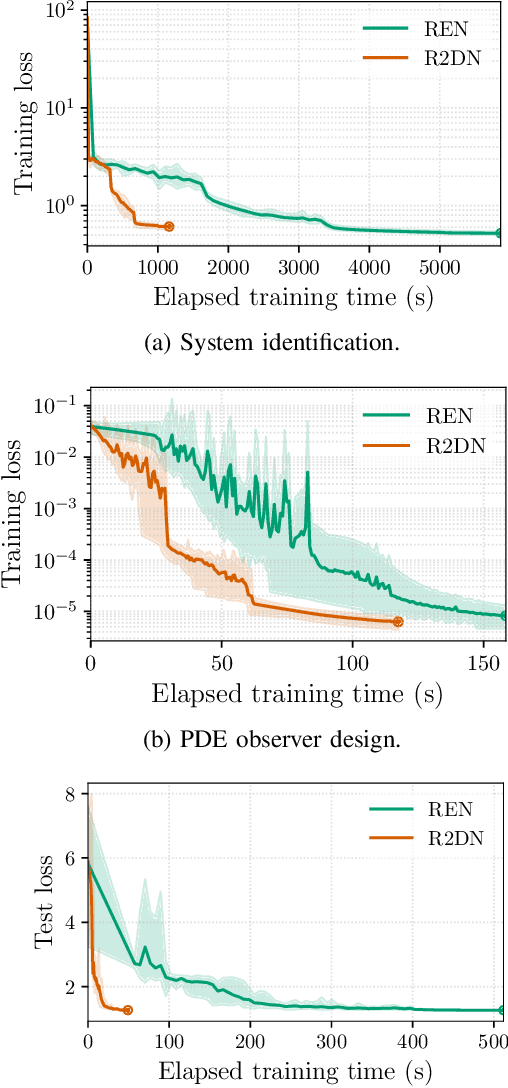
This paper presents the Robust Recurrent Deep Network (R2DN), a scalable parameterization of robust recurrent neural networks for machine learning and data-driven control. We construct R2DNs as a feedback interconnection of a linear time-invariant system and a 1-Lipschitz deep feedforward network, and directly parameterize the weights so that our models are stable (contracting) and robust to small input perturbations (Lipschitz) by design. Our parameterization uses a structure similar to the previously-proposed recurrent equilibrium networks (RENs), but without the requirement to iteratively solve an equilibrium layer at each time-step. This speeds up model evaluation and backpropagation on GPUs, and makes it computationally feasible to scale up the network size, batch size, and input sequence length in comparison to RENs. We compare R2DNs to RENs on three representative problems in nonlinear system identification, observer design, and learning-based feedback control and find that training and inference are both up to an order of magnitude faster with similar test set performance, and that training/inference times scale more favorably with respect to model expressivity.

Norm-Bounded Low-Rank Adaptation

In this work, we propose norm-bounded low-rank adaptation (NB-LoRA) for parameter-efficient fine tuning. We introduce two parameterizations that allow explicit bounds on each singular value of the weight adaptation matrix, which can therefore satisfy any prescribed unitarily invariant norm bound, including the Schatten norms (e.g., nuclear, Frobenius, spectral norm). The proposed parameterizations are unconstrained and complete, i.e. they cover all matrices satisfying the prescribed rank and norm constraints. Experiments on vision fine-tuning benchmarks show that the proposed approach can achieve good adaptation performance while avoiding model catastrophic forgetting and also substantially improve robustness to a wide range of hyper-parameters, including adaptation rank, learning rate and number of training epochs. We also explore applications in privacy-preserving model merging and low-rank matrix completion.

LipKernel: Lipschitz-Bounded Convolutional Neural Networks via Dissipative Layers

We propose a novel layer-wise parameterization for convolutional neural networks (CNNs) that includes built-in robustness guarantees by enforcing a prescribed Lipschitz bound. Each layer in our parameterization is designed to satisfy a linear matrix inequality (LMI), which in turn implies dissipativity with respect to a specific supply rate. Collectively, these layer-wise LMIs ensure Lipschitz boundedness for the input-output mapping of the neural network, yielding a more expressive parameterization than through spectral bounds or orthogonal layers. Our new method LipKernel directly parameterizes dissipative convolution kernels using a 2-D Roesser-type state space model. This means that the convolutional layers are given in standard form after training and can be evaluated without computational overhead. In numerical experiments, we show that the run-time using our method is orders of magnitude faster than state-of-the-art Lipschitz-bounded networks that parameterize convolutions in the Fourier domain, making our approach particularly attractive for improving robustness of learning-based real-time perception or control in robotics, autonomous vehicles, or automation systems. We focus on CNNs, and in contrast to previous works, our approach accommodates a wide variety of layers typically used in CNNs, including 1-D and 2-D convolutional layers, maximum and average pooling layers, as well as strided and dilated convolutions and zero padding. However, our approach naturally extends beyond CNNs as we can incorporate any layer that is incrementally dissipative.

On Robust Reinforcement Learning with Lipschitz-Bounded Policy Networks

This paper presents a study of robust policy networks in deep reinforcement learning. We investigate the benefits of policy parameterizations that naturally satisfy constraints on their Lipschitz bound, analyzing their empirical performance and robustness on two representative problems: pendulum swing-up and Atari Pong. We illustrate that policy networks with small Lipschitz bounds are significantly more robust to disturbances, random noise, and targeted adversarial attacks than unconstrained policies composed of vanilla multi-layer perceptrons or convolutional neural networks. Moreover, we find that choosing a policy parameterization with a non-conservative Lipschitz bound and an expressive, nonlinear layer architecture gives the user much finer control over the performance-robustness trade-off than existing state-of-the-art methods based on spectral normalization.

Learning Stable and Passive Neural Differential Equations

In this paper, we introduce a novel class of neural differential equation, which are intrinsically Lyapunov stable, exponentially stable or passive. We take a recently proposed Polyak Lojasiewicz network (PLNet) as an Lyapunov function and then parameterize the vector field as the descent directions of the Lyapunov function. The resulting models have a same structure as the general Hamiltonian dynamics, where the Hamiltonian is lower- and upper-bounded by quadratic functions. Moreover, it is also positive definite w.r.t. either a known or learnable equilibrium. We illustrate the effectiveness of the proposed model on a damped double pendulum system.

Monotone, Bi-Lipschitz, and Polyak-Lojasiewicz Networks

This paper presents a new \emph{bi-Lipschitz} invertible neural network, the BiLipNet, which has the ability to control both its \emph{Lipschitzness} (output sensitivity to input perturbations) and \emph{inverse Lipschitzness} (input distinguishability from different outputs). The main contribution is a novel invertible residual layer with certified strong monotonicity and Lipschitzness, which we compose with orthogonal layers to build bi-Lipschitz networks. The certification is based on incremental quadratic constraints, which achieves much tighter bounds compared to spectral normalization. Moreover, we formulate the model inverse calculation as a three-operator splitting problem, for which fast algorithms are known. Based on the proposed bi-Lipschitz network, we introduce a new scalar-output network, the PLNet, which satisfies the Polyak-\L{}ojasiewicz condition. It can be applied to learn non-convex surrogate losses with favourable properties, e.g., a unique and efficiently-computable global minimum.

RobustNeuralNetworks.jl: a Package for Machine Learning and Data-Driven Control with Certified Robustness

Neural networks are typically sensitive to small input perturbations, leading to unexpected or brittle behaviour. We present RobustNeuralNetworks.jl: a Julia package for neural network models that are constructed to naturally satisfy a set of user-defined robustness constraints. The package is based on the recently proposed Recurrent Equilibrium Network (REN) and Lipschitz-Bounded Deep Network (LBDN) model classes, and is designed to interface directly with Julia's most widely-used machine learning package, Flux.jl. We discuss the theory behind our model parameterization, give an overview of the package, and provide a tutorial demonstrating its use in image classification, reinforcement learning, and nonlinear state-observer design.

Learning Over All Contracting and Lipschitz Closed-Loops for Partially-Observed Nonlinear Systems

This paper presents a policy parameterization for learning-based control on nonlinear, partially-observed dynamical systems. The parameterization is based on a nonlinear version of the Youla parameterization and the recently proposed Recurrent Equilibrium Network (REN) class of models. We prove that the resulting Youla-REN parameterization automatically satisfies stability (contraction) and user-tunable robustness (Lipschitz) conditions on the closed-loop system. This means it can be used for safe learning-based control with no additional constraints or projections required to enforce stability or robustness. We test the new policy class in simulation on two reinforcement learning tasks: 1) magnetic suspension, and 2) inverting a rotary-arm pendulum. We find that the Youla-REN performs similarly to existing learning-based and optimal control methods while also ensuring stability and exhibiting improved robustness to adversarial disturbances.