Un-regularizing: approximate proximal point and faster stochastic algorithms for empirical risk minimization

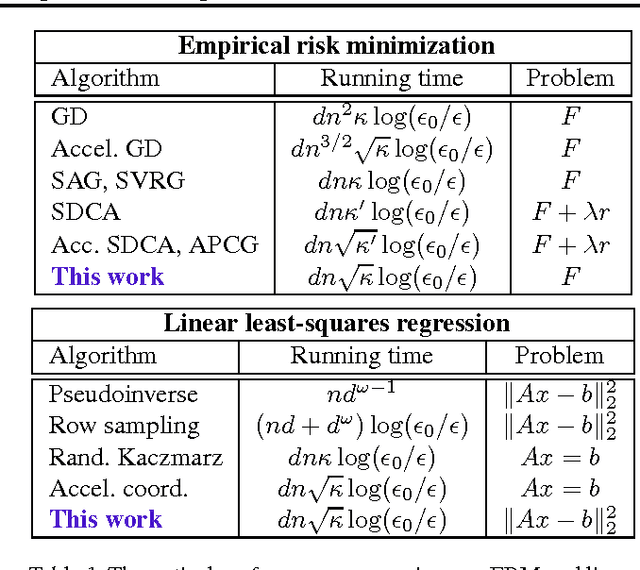
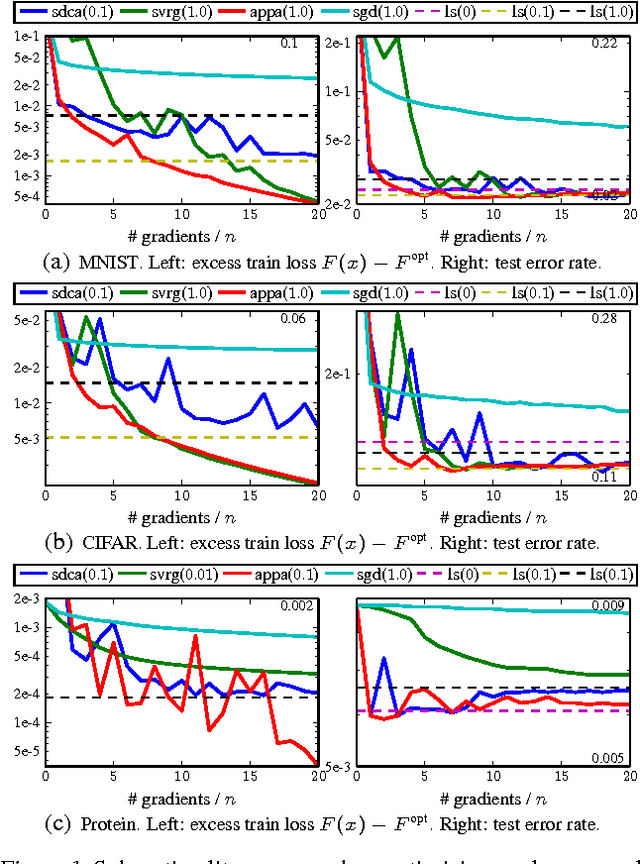
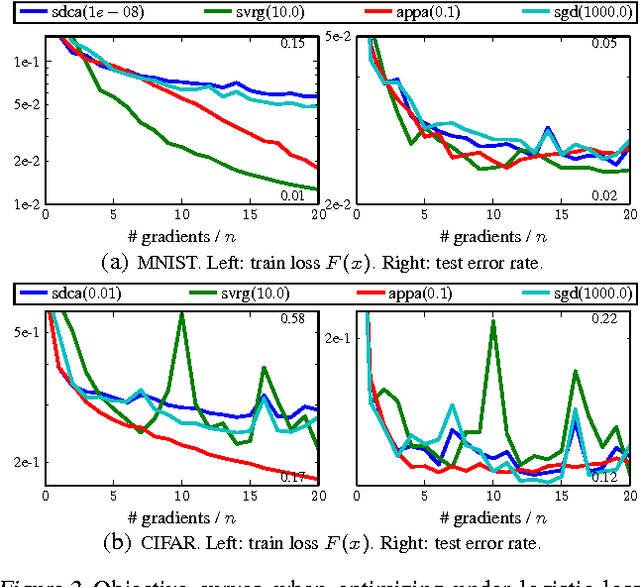
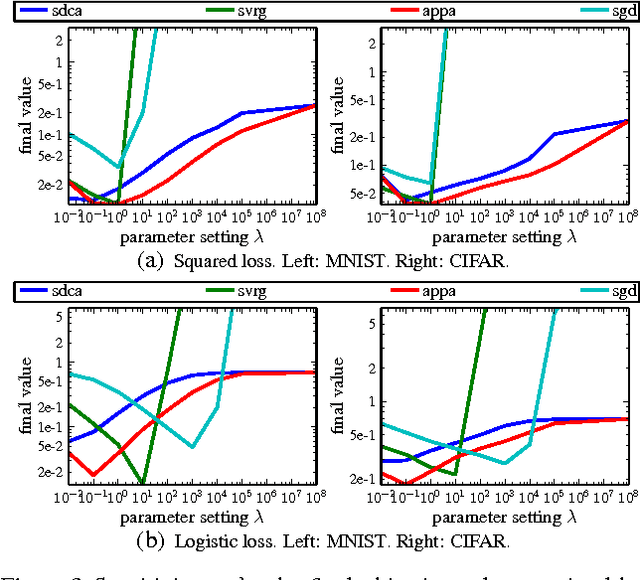
We develop a family of accelerated stochastic algorithms that minimize sums of convex functions. Our algorithms improve upon the fastest running time for empirical risk minimization (ERM), and in particular linear least-squares regression, across a wide range of problem settings. To achieve this, we establish a framework based on the classical proximal point algorithm. Namely, we provide several algorithms that reduce the minimization of a strongly convex function to approximate minimizations of regularizations of the function. Using these results, we accelerate recent fast stochastic algorithms in a black-box fashion. Empirically, we demonstrate that the resulting algorithms exhibit notions of stability that are advantageous in practice. Both in theory and in practice, the provided algorithms reap the computational benefits of adding a large strongly convex regularization term, without incurring a corresponding bias to the original problem.

Competing with the Empirical Risk Minimizer in a Single Pass

In many estimation problems, e.g. linear and logistic regression, we wish to minimize an unknown objective given only unbiased samples of the objective function. Furthermore, we aim to achieve this using as few samples as possible. In the absence of computational constraints, the minimizer of a sample average of observed data -- commonly referred to as either the empirical risk minimizer (ERM) or the $M$-estimator -- is widely regarded as the estimation strategy of choice due to its desirable statistical convergence properties. Our goal in this work is to perform as well as the ERM, on every problem, while minimizing the use of computational resources such as running time and space usage. We provide a simple streaming algorithm which, under standard regularity assumptions on the underlying problem, enjoys the following properties: * The algorithm can be implemented in linear time with a single pass of the observed data, using space linear in the size of a single sample. * The algorithm achieves the same statistical rate of convergence as the empirical risk minimizer on every problem, even considering constant factors. * The algorithm's performance depends on the initial error at a rate that decreases super-polynomially. * The algorithm is easily parallelizable. Moreover, we quantify the (finite-sample) rate at which the algorithm becomes competitive with the ERM.

Relaxations for inference in restricted Boltzmann machines

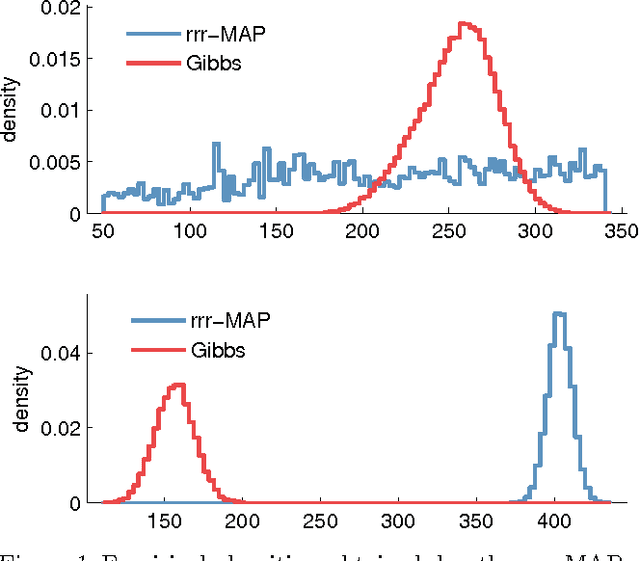
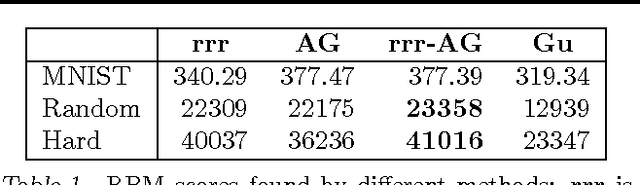
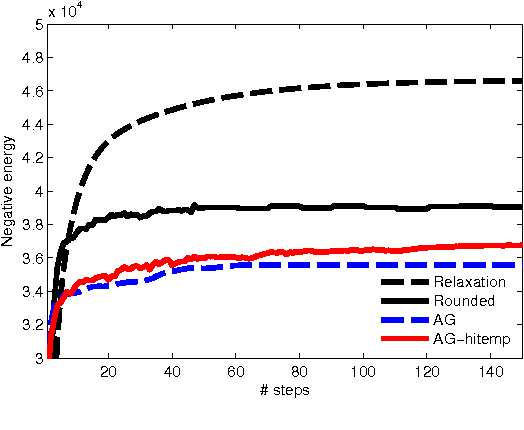
We propose a relaxation-based approximate inference algorithm that samples near-MAP configurations of a binary pairwise Markov random field. We experiment on MAP inference tasks in several restricted Boltzmann machines. We also use our underlying sampler to estimate the log-partition function of restricted Boltzmann machines and compare against other sampling-based methods.