Conical Localization via Modified Polar Representation: A Unified Framework for Robust 3-D Positioning with 1-D Sensor Arrays

This paper presents a unified framework for robust three-dimensional (3-D) source localization using a network of sensors equipped with one-dimensional (1-D) linear arrays. While such arrays offer practical advantages in terms of cost and size, existing localization methods suffer from a fundamental limitation: their performance degrades significantly as the source moves into the far-field, a common challenge known as the thresholding effect. To address this issue, we reformulate the localization problem in the modified polar representation (MPR) coordinate system, which parameterizes the source location using its azimuth, elevation, and inverse-range. We have developed a constrained weighted least squares (CWLS) estimator, which is subsequently transformed into a tight semidefinite programming (SDP) problem via semidefinite relaxation, enhanced with additional constraints to improve accuracy. Simulation results demonstrate that the proposed estimator attains the Cramer-Rao lower bound (CRLB) for both angle and inverse-range estimation in near-field scenarios. More importantly, it maintains this optimal performance in the far-field, substantially outperforming state-of-the-art methods, which exhibit significant error at large ranges. The proposed solution thus provides a reliable, unified localization system that is effective irrespective of the source range.

Fundamental Performance Bounds for Carrier Phase Positioning in Cellular Networks

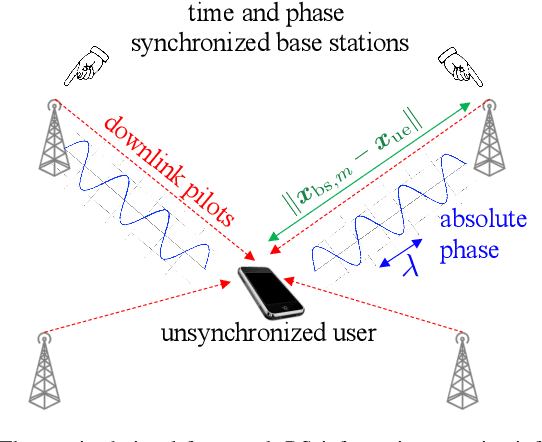
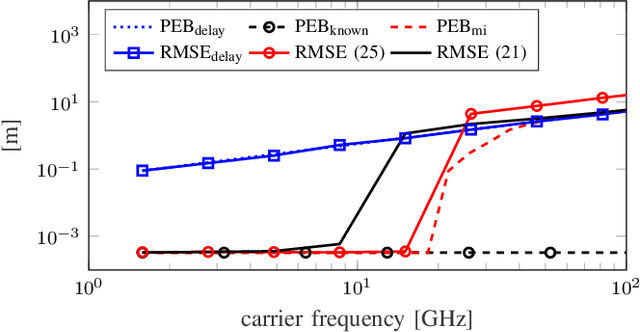
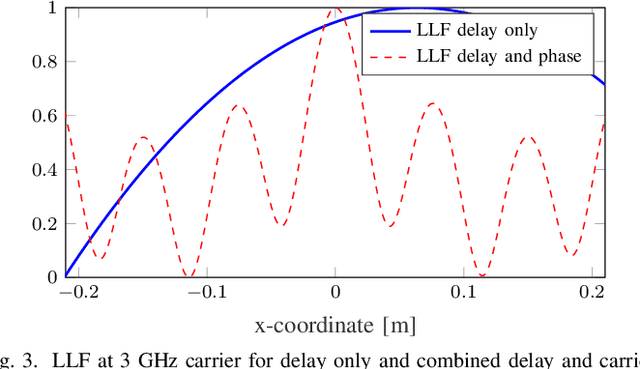
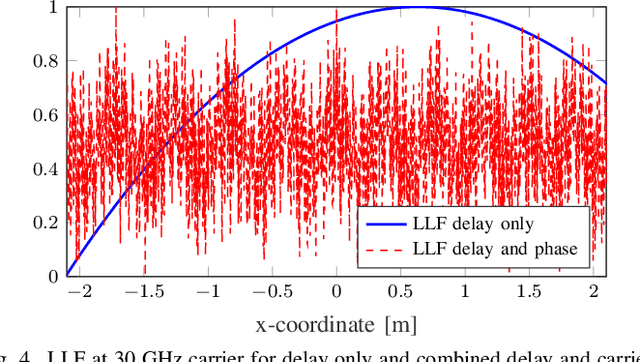
The carrier phase of cellular signals can be utilized for highly accurate positioning, with the potential for orders-of-magnitude performance improvements compared to standard time-difference-of-arrival positioning. Due to the integer ambiguities, standard performance evaluation tools such as the Cram\'er-Rao bound (CRB) are overly optimistic. In this paper, a new performance bound, called the mixed-integer CRB (MICRB) is introduced that explicitly accounts for this integer ambiguity. While computationally more complex than the standard CRB, the MICRB can accurately predict positioning performance, as verified by numerical simulations.

Sparsity Domain Smoothing Based Thresholding Recovery Method for OFDM Sparse Channel Estimation

Due to the ever increasing data rate demand of beyond 5G networks and considering the wide range of Orthogonal Frequency Division Multipllexing (OFDM) technique in cellular systems, it is critical to reduce pilot overhead of OFDM systems in order to increase data rate of such systems. Due to sparsity of multipath channels, sparse recovery methods can be exploited to reduce pilot overhead. OFDM pilots are utilized as random samples for channel impulse response estimation. We propose a three-step sparsity recovery algorithm which is based on sparsity domain smoothing. Time domain residue computation, sparsity domain smoothing, and adaptive thresholding sparsifying are the three-steps of the proposed scheme. To the best of our knowledge, the proposed sparsity domain smoothing based thresholding recovery method known as SDS-IMAT has not been used for OFDM sparse channel estimation in the literature. Pilot locations are also derived based on the minimization of the measurement matrix coherence. Numerical results verify that the performance of the proposed scheme outperforms other existing thresholding and greedy recovery methods and has a near-optimal performance. The effectiveness of the proposed scheme is shown in terms of mean square error and bit error rate.