Wind Power Scenario Generation based on the Generalized Dynamic Factor Model and Generative Adversarial Network

For conducting resource adequacy studies, we synthesize multiple long-term wind power scenarios of distributed wind farms simultaneously by using the spatio-temporal features: spatial and temporal correlation, waveforms, marginal and ramp rates distributions of waveform, power spectral densities, and statistical characteristics. Generating the spatial correlation in scenarios requires the design of common factors for neighboring wind farms and antithetical factors for distant wind farms. The generalized dynamic factor model (GDFM) can extract the common factors through cross spectral density analysis, but it cannot closely imitate waveforms. The GAN can synthesize plausible samples representing the temporal correlation by verifying samples through a fake sample discriminator. To combine the advantages of GDFM and GAN, we use the GAN to provide a filter that extracts dynamic factors with temporal information from the observation data, and we then apply this filter in the GDFM to represent both spatial and frequency correlations of plausible waveforms. Numerical tests on the combination of GDFM and GAN have demonstrated performance improvements over competing alternatives in synthesizing wind power scenarios from Australia, better realizing plausible statistical characteristics of actual wind power compared to alternatives such as the GDFM with a filter synthesized from distributions of actual dynamic filters and the GAN with direct synthesis without dynamic factors.

Online Energy Price Matrix Factorization for Power Grid Topology Tracking

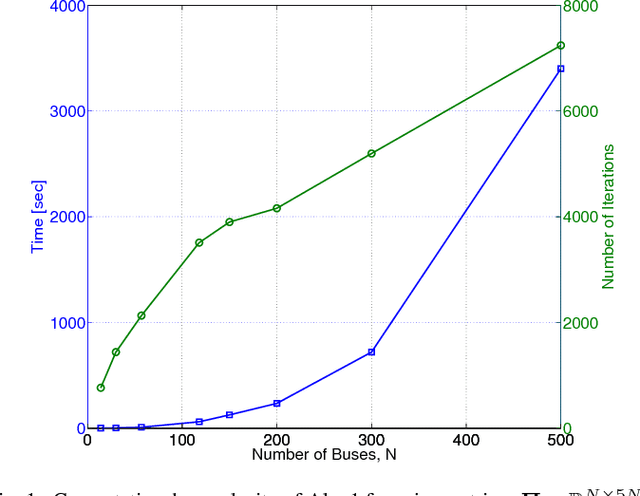
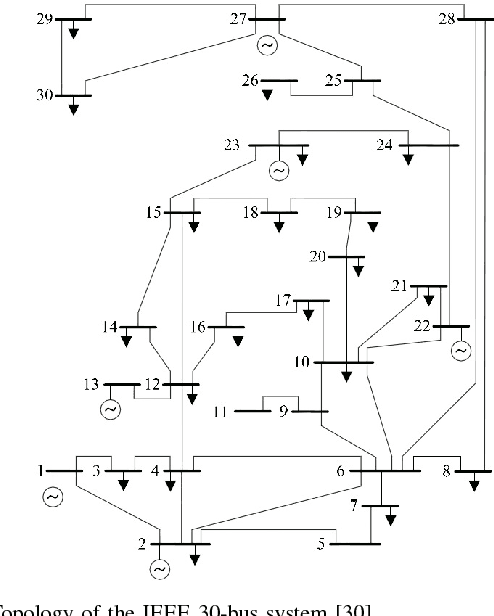
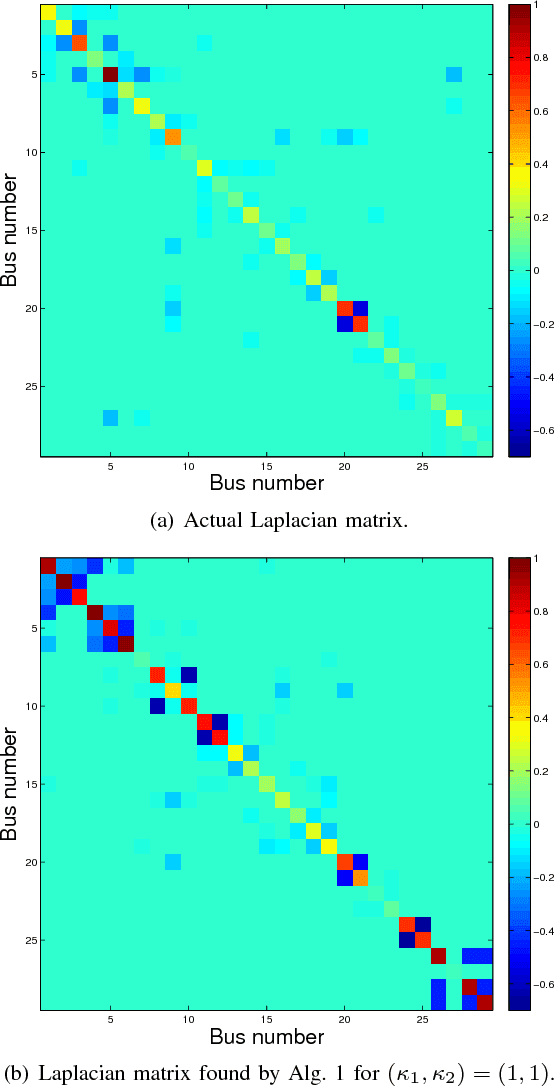
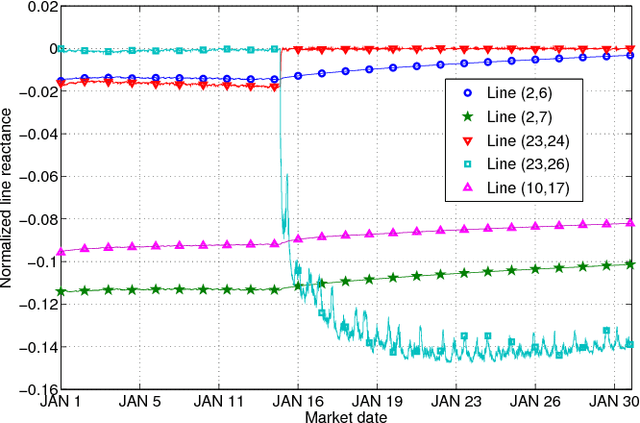
Grid security and open markets are two major smart grid goals. Transparency of market data facilitates a competitive and efficient energy environment, yet it may also reveal critical physical system information. Recovering the grid topology based solely on publicly available market data is explored here. Real-time energy prices are calculated as the Lagrange multipliers of network-constrained economic dispatch; that is, via a linear program (LP) typically solved every 5 minutes. Granted the grid Laplacian is a parameter of this LP, one could infer such a topology-revealing matrix upon observing successive LP dual outcomes. The matrix of spatio-temporal prices is first shown to factor as the product of the inverse Laplacian times a sparse matrix. Leveraging results from sparse matrix decompositions, topology recovery schemes with complementary strengths are subsequently formulated. Solvers scalable to high-dimensional and streaming market data are devised. Numerical validation using real load data on the IEEE 30-bus grid provide useful input for current and future market designs.

Grid Topology Identification using Electricity Prices

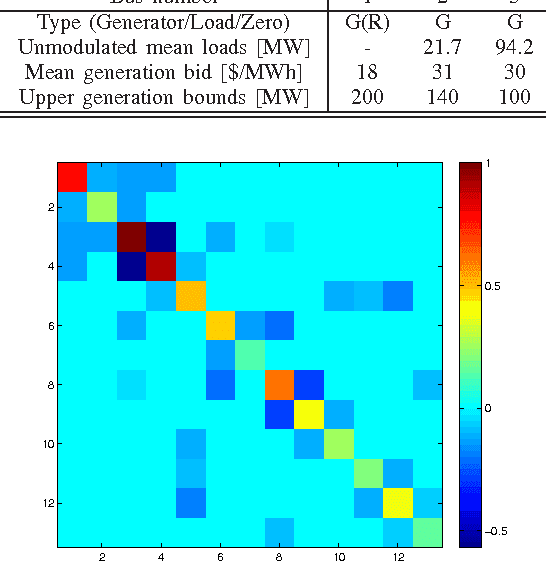
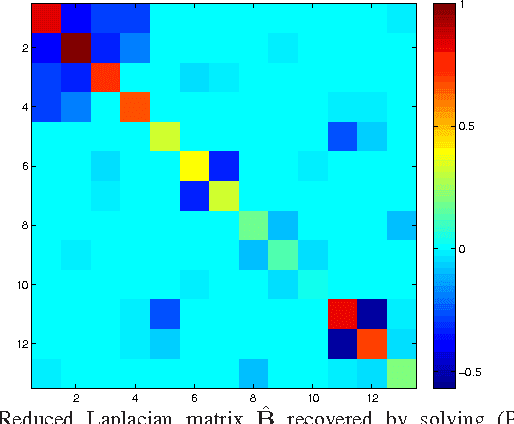
The potential of recovering the topology of a grid using solely publicly available market data is explored here. In contemporary whole-sale electricity markets, real-time prices are typically determined by solving the network-constrained economic dispatch problem. Under a linear DC model, locational marginal prices (LMPs) correspond to the Lagrange multipliers of the linear program involved. The interesting observation here is that the matrix of spatiotemporally varying LMPs exhibits the following property: Once premultiplied by the weighted grid Laplacian, it yields a low-rank and sparse matrix. Leveraging this rich structure, a regularized maximum likelihood estimator (MLE) is developed to recover the grid Laplacian from the LMPs. The convex optimization problem formulated includes low rank- and sparsity-promoting regularizers, and it is solved using a scalable algorithm. Numerical tests on prices generated for the IEEE 14-bus benchmark provide encouraging topology recovery results.