Sample and Communication-Efficient Decentralized Actor-Critic Algorithms with Finite-Time Analysis

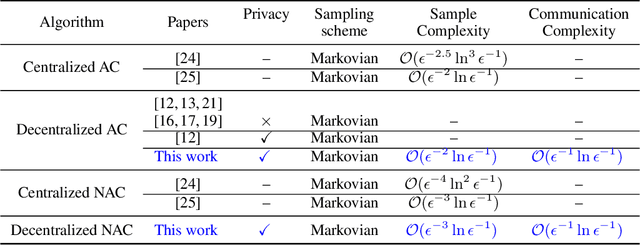
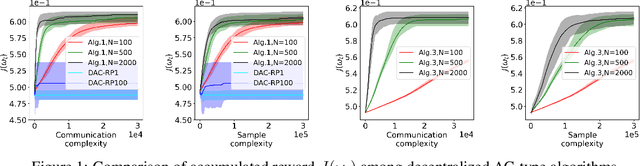
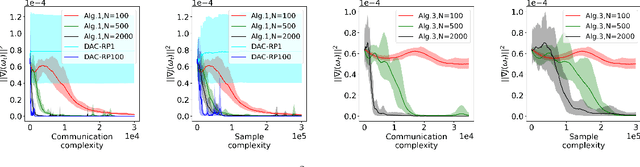
Actor-critic (AC) algorithms have been widely adopted in decentralized multi-agent systems to learn the optimal joint control policy. However, existing decentralized AC algorithms either do not preserve the privacy of agents or are not sample and communication-efficient. In this work, we develop two decentralized AC and natural AC (NAC) algorithms that are private, and sample and communication-efficient. In both algorithms, agents share noisy information to preserve privacy and adopt mini-batch updates to improve sample and communication efficiency. Particularly for decentralized NAC, we develop a decentralized Markovian SGD algorithm with an adaptive mini-batch size to efficiently compute the natural policy gradient. Under Markovian sampling and linear function approximation, we prove the proposed decentralized AC and NAC algorithms achieve the state-of-the-art sample complexities $\mathcal{O}\big(\epsilon^{-2}\ln(\epsilon^{-1})\big)$ and $\mathcal{O}\big(\epsilon^{-3}\ln(\epsilon^{-1})\big)$, respectively, and the same small communication complexity $\mathcal{O}\big(\epsilon^{-1}\ln(\epsilon^{-1})\big)$. Numerical experiments demonstrate that the proposed algorithms achieve lower sample and communication complexities than the existing decentralized AC algorithm.

Multi-Agent Off-Policy TD Learning: Finite-Time Analysis with Near-Optimal Sample Complexity and Communication Complexity

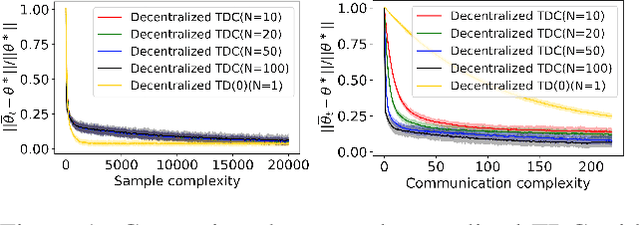
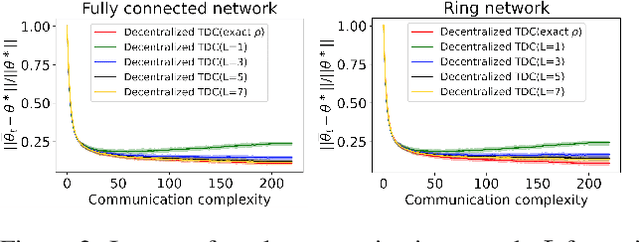
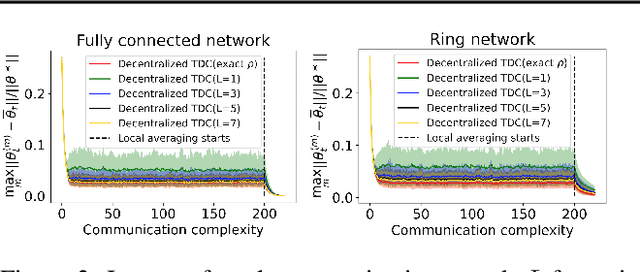
The finite-time convergence of off-policy TD learning has been comprehensively studied recently. However, such a type of convergence has not been well established for off-policy TD learning in the multi-agent setting, which covers broader applications and is fundamentally more challenging. This work develops two decentralized TD with correction (TDC) algorithms for multi-agent off-policy TD learning under Markovian sampling. In particular, our algorithms preserve full privacy of the actions, policies and rewards of the agents, and adopt mini-batch sampling to reduce the sampling variance and communication frequency. Under Markovian sampling and linear function approximation, we proved that the finite-time sample complexity of both algorithms for achieving an $\epsilon$-accurate solution is in the order of $\mathcal{O}(\epsilon^{-1}\ln \epsilon^{-1})$, matching the near-optimal sample complexity of centralized TD(0) and TDC. Importantly, the communication complexity of our algorithms is in the order of $\mathcal{O}(\ln \epsilon^{-1})$, which is significantly lower than the communication complexity $\mathcal{O}(\epsilon^{-1}\ln \epsilon^{-1})$ of the existing decentralized TD(0). Experiments corroborate our theoretical findings.