Learning Nonlinear Loop Invariants with Gated Continuous Logic Networks

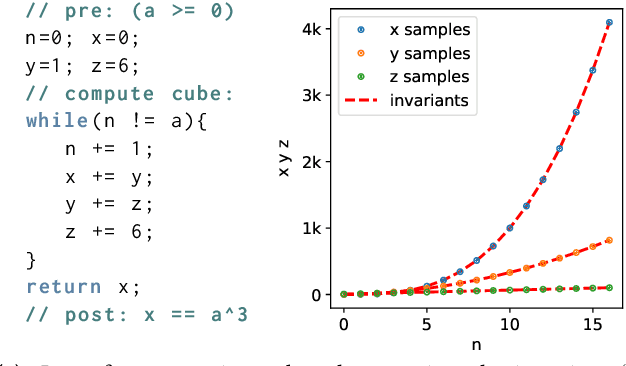
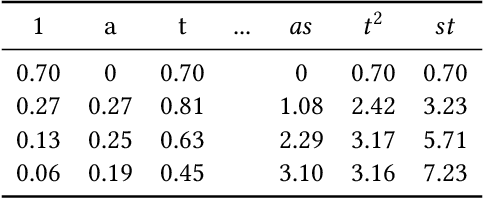
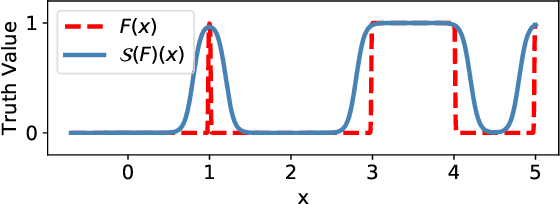
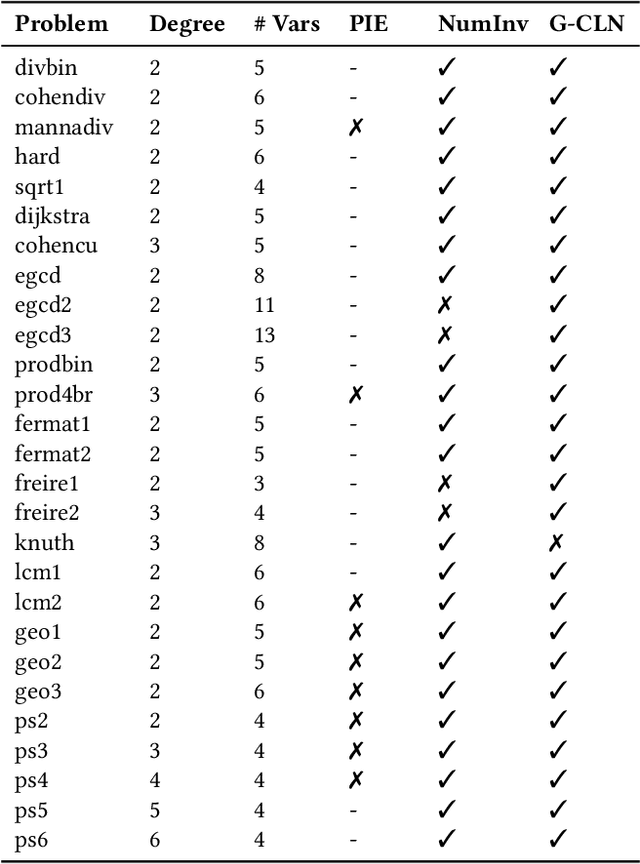
Verifying real-world programs often requires inferring loop invariants with nonlinear constraints. This is especially true in programs that perform many numerical operations, such as control systems for avionics or industrial plants. Recently, data-driven methods for loop invariant inference have shown promise, especially on linear invariants. However, applying data-driven inference to nonlinear loop invariants is challenging due to the large numbers of and magnitudes of high-order terms, the potential for overfitting on a small number of samples, and the large space of possible inequality bounds. In this paper, we introduce a new neural architecture for general SMT learning, the Gated Continuous Logic Network (G-CLN), and apply it to nonlinear loop invariant learning. G-CLNs extend the Continuous Logic Network (CLN) architecture with gating units and dropout, which allow the model to robustly learn general invariants over large numbers of terms. To address overfitting that arises from finite program sampling, we introduce fractional sampling---a sound relaxation of loop semantics to continuous functions that facilitates unbounded sampling on real domain. We additionally design a new CLN activation function, the Piecewise Biased Quadratic Unit (PBQU), for naturally learning tight inequality bounds. We incorporate these methods into a nonlinear loop invariant inference system that can learn general nonlinear loop invariants. We evaluate our system on a benchmark of nonlinear loop invariants and show it solves 26 out of 27 problems, 3 more than prior work, with an average runtime of 53.3 seconds. We further demonstrate the generic learning ability of G-CLNs by solving all 124 problems in the linear Code2Inv benchmark. We also perform a quantitative stability evaluation and show G-CLNs have a convergence rate of $97.5\%$ on quadratic problems, a $39.2\%$ improvement over CLN models.

CLN2INV: Learning Loop Invariants with Continuous Logic Networks

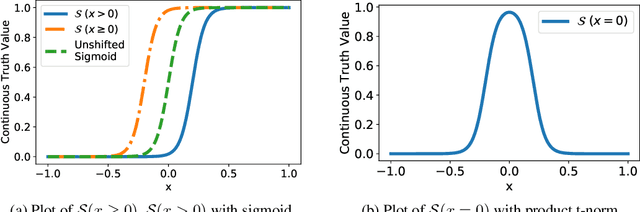
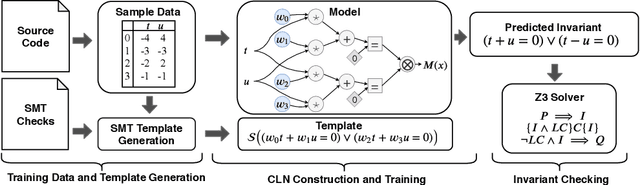
Program verification offers a framework for ensuring program correctness and therefore systematically eliminating different classes of bugs. Inferring loop invariants is one of the main challenges behind automated verification of real-world programs which often contain many loops. In this paper, we present Continuous Logic Network (CLN), a novel neural architecture for automatically learning loop invariants directly from program execution traces. Unlike existing neural networks, CLNs can learn precise and explicit representations of formulas in Satisfiability Modulo Theories (SMT) for loop invariants from program execution traces. We develop a new sound and complete semantic mapping for assigning SMT formulas to continuous truth values that allows CLNs to be trained efficiently. We use CLNs to implement a new inference system for loop invariants, CLN2INV, that significantly outperforms existing approaches on the popular Code2Inv dataset. CLN2INV is the first tool to solve all 124 theoretically solvable problems in the Code2Inv dataset. Moreover, CLN2INV takes only 1.1 seconds on average for each problem, which is 40 times faster than existing approaches. We further demonstrate that CLN2INV can even learn 12 significantly more complex loop invariants than the ones required for the Code2Inv dataset.