A posteriori learning of quasi-geostrophic turbulence parametrization: an experiment on integration steps

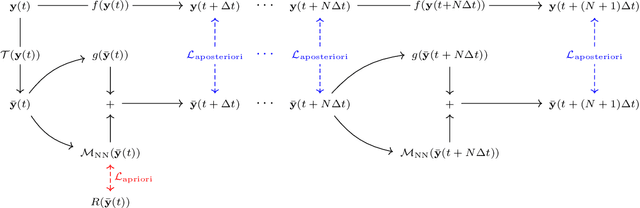
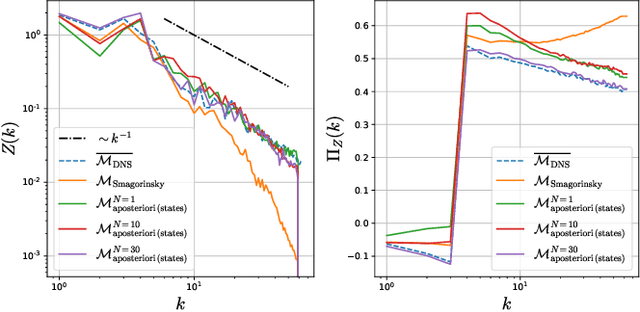
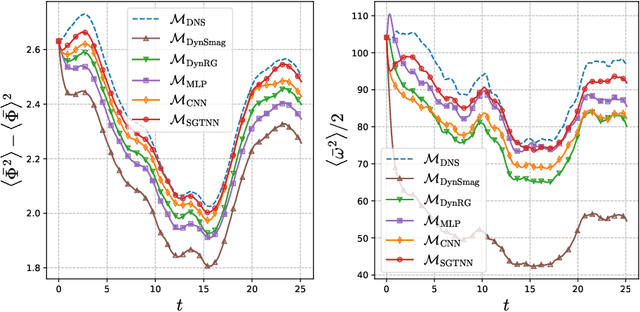
Modeling the subgrid-scale dynamics of reduced models is a long standing open problem that finds application in ocean, atmosphere and climate predictions where direct numerical simulation (DNS) is impossible. While neural networks (NNs) have already been applied to a range of three-dimensional flows with success, two dimensional flows are more challenging because of the backscatter of energy from small to large scales. We show that learning a model jointly with the dynamical solver and a meaningful \textit{a posteriori}-based loss function lead to stable and realistic simulations when applied to quasi-geostrophic turbulence.

Joint calibration and mapping of satellite altimetry data using trainable variational models

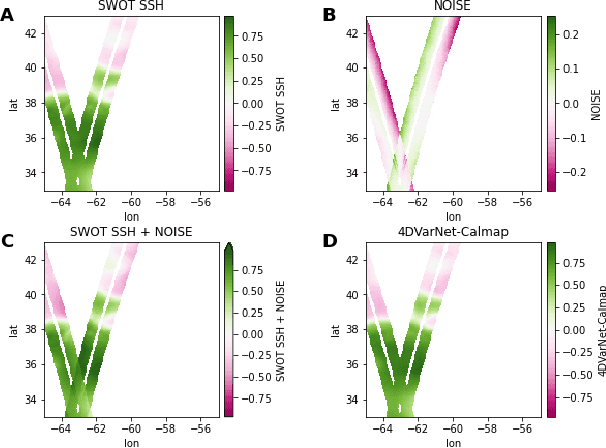
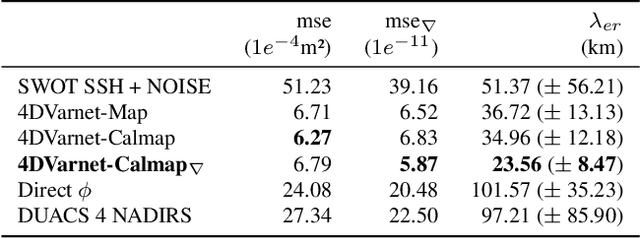
Satellite radar altimeters are a key source of observation of ocean surface dynamics. However, current sensor technology and mapping techniques do not yet allow to systematically resolve scales smaller than 100km. With their new sensors, upcoming wide-swath altimeter missions such as SWOT should help resolve finer scales. Current mapping techniques rely on the quality of the input data, which is why the raw data go through multiple preprocessing stages before being used. Those calibration stages are improved and refined over many years and represent a challenge when a new type of sensor start acquiring data. Here we show how a data-driven variational data assimilation framework could be used to jointly learn a calibration operator and an interpolator from non-calibrated data . The proposed framework significantly outperforms the operational state-of-the-art mapping pipeline and truly benefits from wide-swath data to resolve finer scales on the global map as well as in the SWOT sensor geometry.

TrAISformer-A generative transformer for AIS trajectory prediction

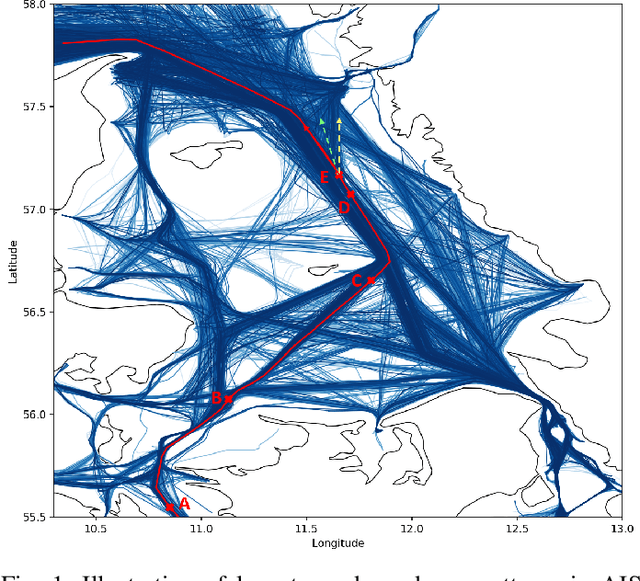
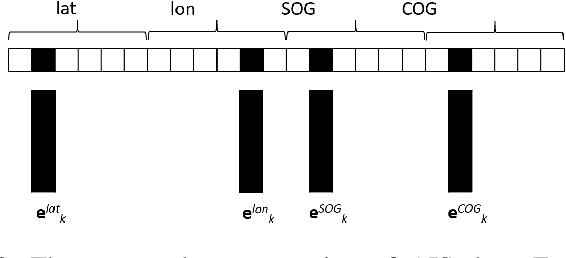
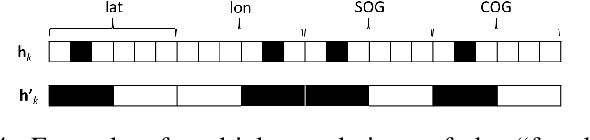
Modelling trajectory in general, and vessel trajectory in particular, is a difficult task because of the multimodal and complex nature of motion data. In this paper, we present TrAISformer-a novel deep learning architecture that can forecast vessel positions using AIS (Automatic Identification System) observations. We address the multimodality by introducing a discrete representation of AIS data and re-frame the prediction, which is originally a regression problem, as a classification problem. The model encodes complex movement patterns in AIS data in high-dimensional vectors, then applies a transformer to extract useful long-term correlations from sequences of those embeddings to sample future vessel positions. Experimental results on real, public AIS data demonstrate that TrAISformer significantly outperforms state-of-the-art methods.

Learning stochastic dynamical systems with neural networks mimicking the Euler-Maruyama scheme

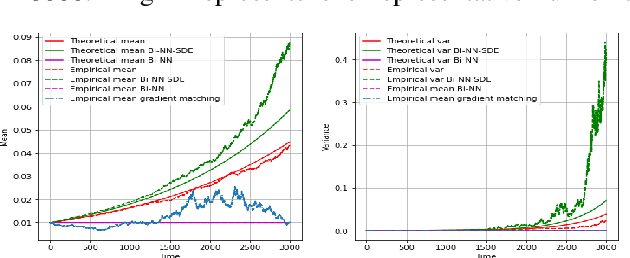
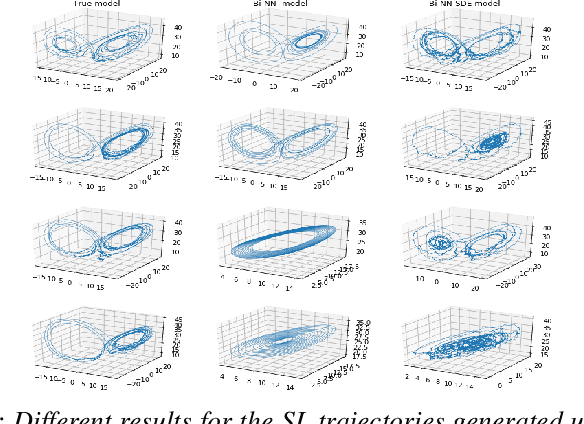
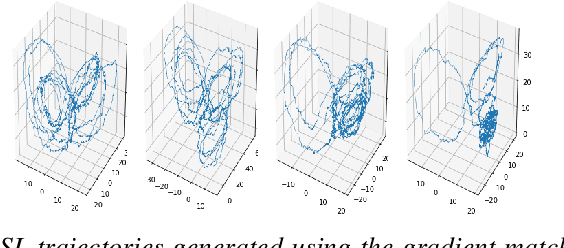
Stochastic differential equations (SDEs) are one of the most important representations of dynamical systems. They are notable for the ability to include a deterministic component of the system and a stochastic one to represent random unknown factors. However, this makes learning SDEs much more challenging than ordinary differential equations (ODEs). In this paper, we propose a data driven approach where parameters of the SDE are represented by a neural network with a built-in SDE integration scheme. The loss function is based on a maximum likelihood criterion, under order one Markov Gaussian assumptions. The algorithm is applied to the geometric brownian motion and a stochastic version of the Lorenz-63 model. The latter is particularly hard to handle due to the presence of a stochastic component that depends on the state. The algorithm performance is attested using different simulations results. Besides, comparisons are performed with the reference gradient matching method used for non linear drift estimation, and a neural networks-based method, that does not consider the stochastic term.

Learning Runge-Kutta Integration Schemes for ODE Simulation and Identification

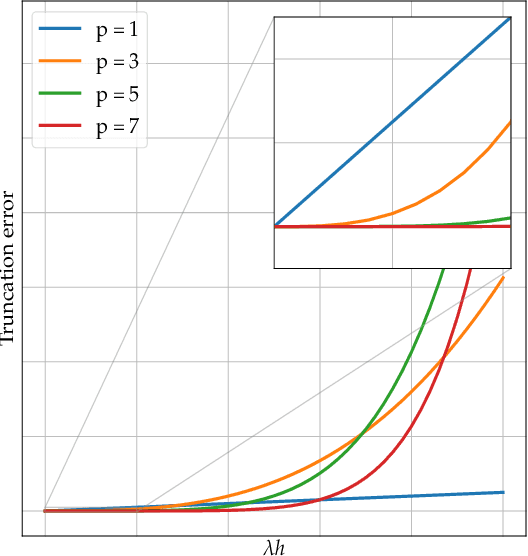
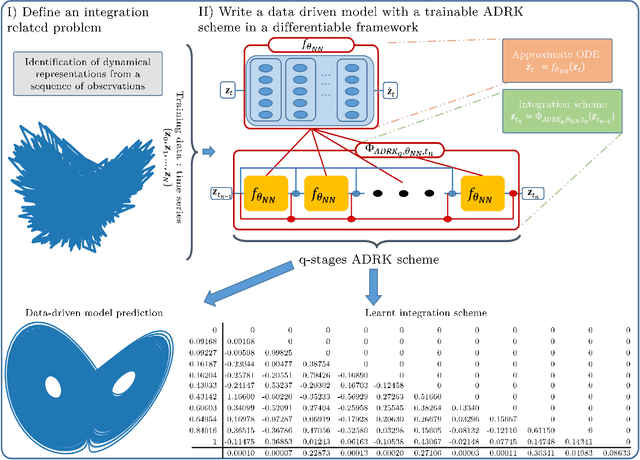
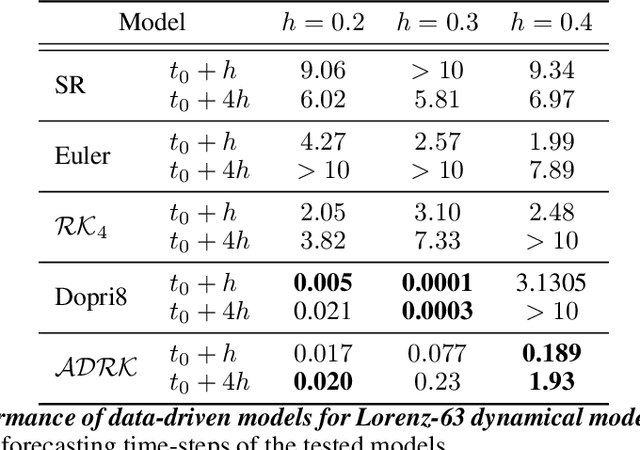
Deriving analytical solutions of ordinary differential equations is usually restricted to a small subset of problems and numerical techniques are considered. Inevitably, a numerical simulation of a differential equation will then always be distinct from a true analytical solution. An efficient integration scheme shall further not only provide a trajectory throughout a given state, but also be derived to ensure the generated simulation to be close to the analytical one. Consequently, several integration schemes were developed for different classes of differential equations. Unfortunately, when considering the integration of complex non-linear systems, as well as the identification of non-linear equations from data, this choice of the integration scheme is often far from being trivial. In this paper, we propose a novel framework to learn integration schemes that minimize an integration-related cost function. We demonstrate the relevance of the proposed learning-based approach for non-linear equations and include a quantitative analysis w.r.t. classical state-of-the-art integration techniques, especially where the latter may not apply.

Physical invariance in neural networks for subgrid-scale scalar flux modeling

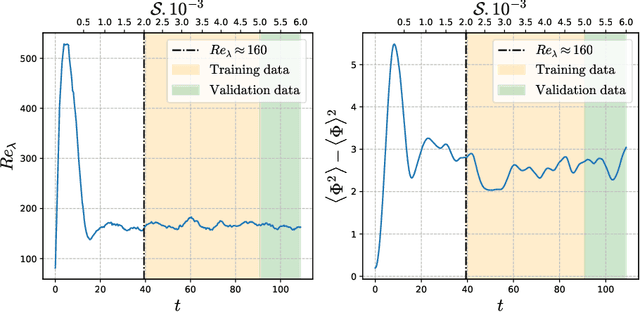
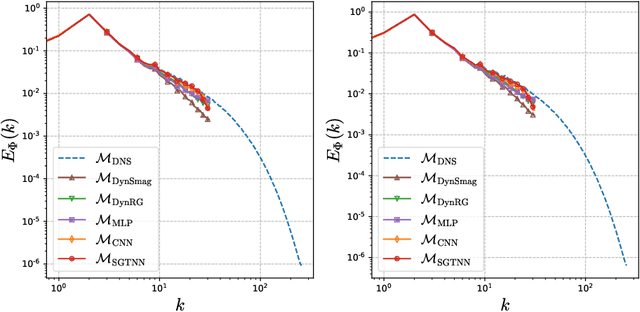
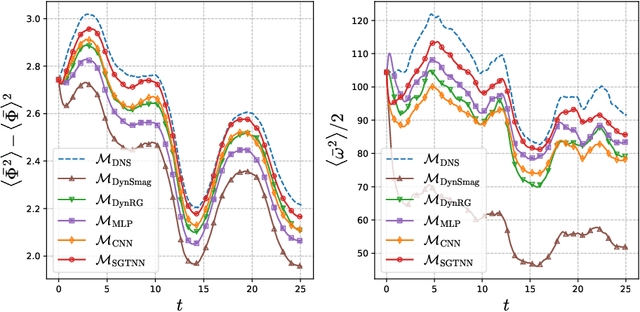
In this paper we present a new strategy to model the subgrid-scale scalar flux in a three-dimensional turbulent incompressible flow using physics-informed neural networks (NNs). When trained from direct numerical simulation (DNS) data, state-of-the-art neural networks, such as convolutional neural networks, may not preserve well known physical priors, which may in turn question their application to real case-studies. To address this issue, we investigate hard and soft constraints into the model based on classical invariances and symmetries derived from physical laws. From simulation-based experiments, we show that the proposed physically-invariant NN model outperforms both purely data-driven ones as well as parametric state-of-the-art subgrid-scale model. The considered invariances are regarded as regularizers on physical metrics during the a priori evaluation and constrain the distribution tails of the predicted subgrid-scale term to be closer to the DNS. They also increase the stability and performance of the model when used as a surrogate during a large-eddy simulation. Moreover, the physically-invariant NN is shown to generalize to configurations that have not been seen during the training phase.

Variational Deep Learning for the Identification and Reconstruction of Chaotic and Stochastic Dynamical Systems from Noisy and Partial Observations

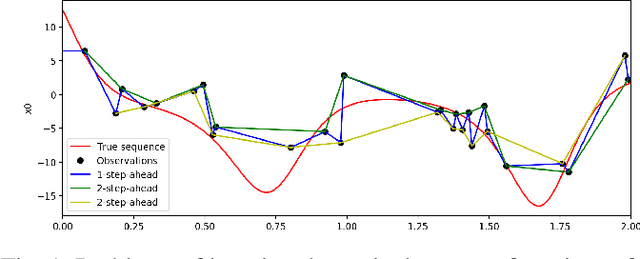
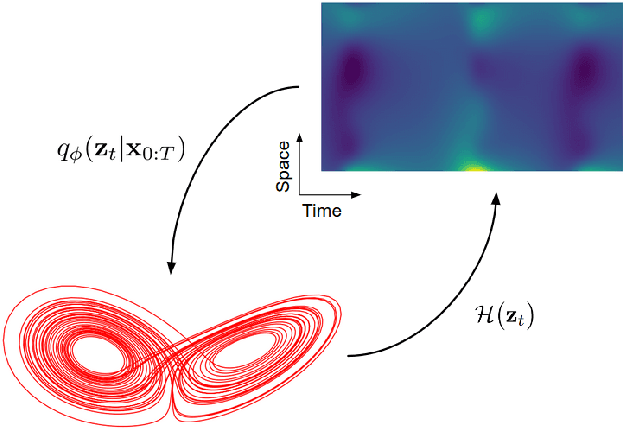
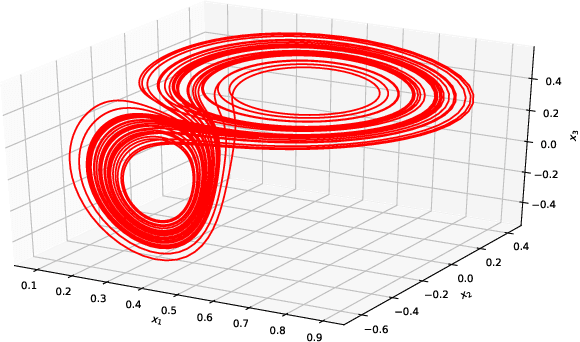
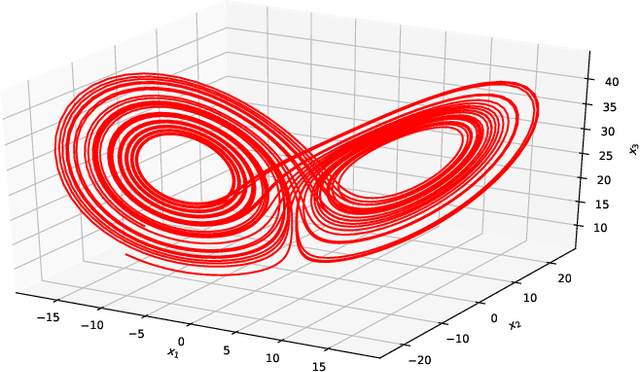
The data-driven recovery of the unknown governing equations of dynamical systems has recently received an increasing interest. However, the identification of the governing equations remains challenging when dealing with noisy and partial observations. Here, we address this challenge and investigate variational deep learning schemes. Within the proposed framework, we jointly learn an inference model to reconstruct the true states of the system from series of noisy and partial data and the governing equations of these states. In doing so, this framework bridges classical data assimilation and state-of-the-art machine learning techniques and we show that it generalizes state-of-the-art methods. Importantly, both the inference model and the governing equations embed stochastic components to account for stochastic variabilities, model errors and reconstruction uncertainties. Various experiments on chaotic and stochastic dynamical systems support the relevance of our scheme w.r.t. state-of-the-art approaches.

Detection of Abnormal Vessel Behaviours from AIS data using GeoTrackNet: from the Laboratory to the Ocean

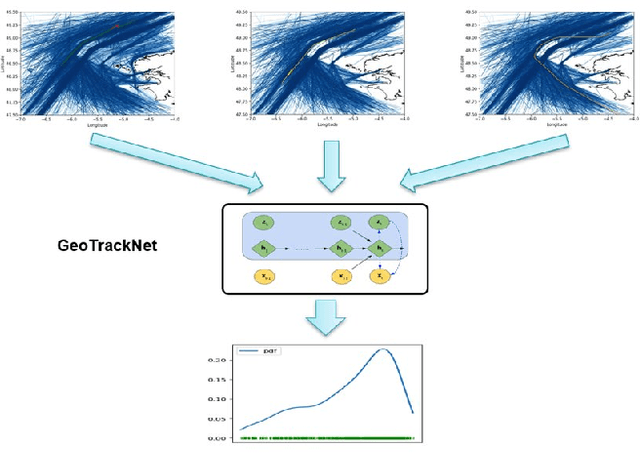
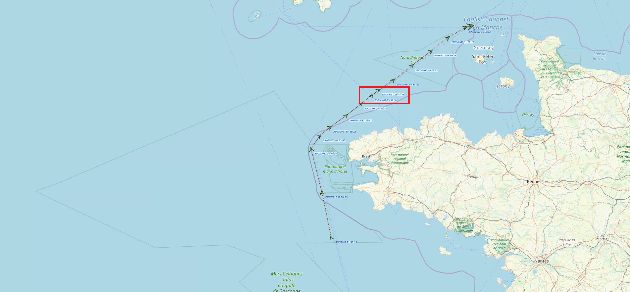
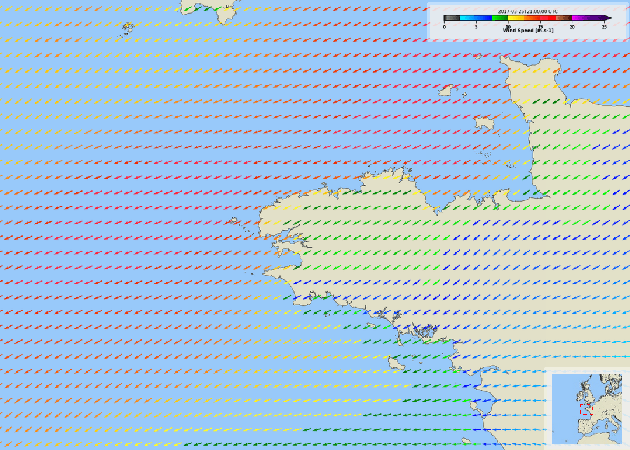
The constant growth of maritime traffic leads to the need of automatic anomaly detection, which has been attracting great research attention. Information provided by AIS (Automatic Identification System) data, together with recent outstanding progresses of deep learning, make vessel monitoring using neural networks (NNs) a very promising approach. This paper analyses a novel neural network we have recently introduced -- GeoTrackNet -- regarding operational contexts. Especially, we aim to evaluate (i) the relevance of the abnormal behaviours detected by GeoTrackNet with respect to expert interpretations, (ii) the extent to which GeoTrackNet may process AIS data streams in real time. We report experiments showing the high potential to meet operational levels of the model.

Learning Variational Data Assimilation Models and Solvers

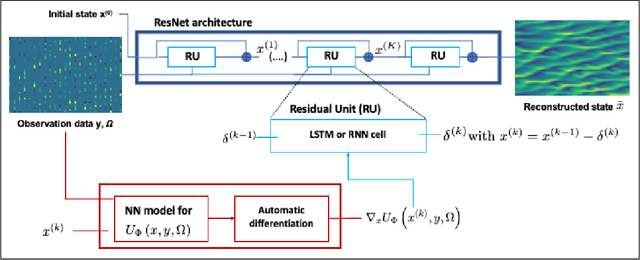
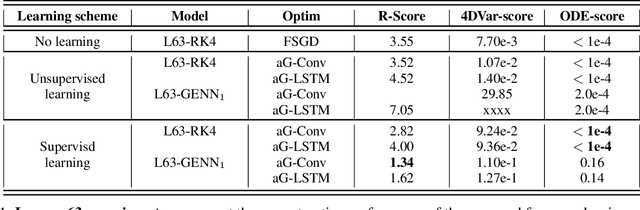
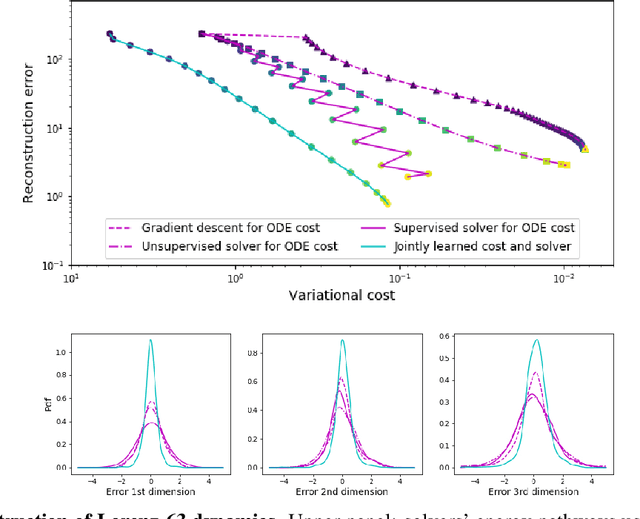
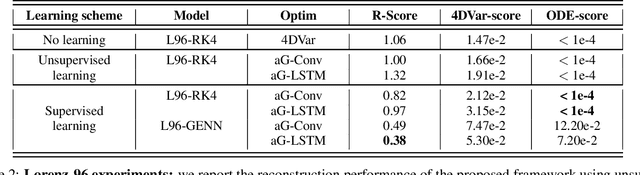
This paper addresses variational data assimilation from a learning point of view. Data assimilation aims to reconstruct the time evolution of some state given a series of observations, possibly noisy and irregularly-sampled. Using automatic differentiation tools embedded in deep learning frameworks, we introduce end-to-end neural network architectures for data assimilation. It comprises two key components: a variational model and a gradient-based solver both implemented as neural networks. A key feature of the proposed end-to-end learning architecture is that we may train the NN models using both supervised and unsupervised strategies. Our numerical experiments on Lorenz-63 and Lorenz-96 systems report significant gain w.r.t. a classic gradient-based minimization of the variational cost both in terms of reconstruction performance and optimization complexity. Intriguingly, we also show that the variational models issued from the true Lorenz-63 and Lorenz-96 ODE representations may not lead to the best reconstruction performance. We believe these results may open new research avenues for the specification of assimilation models in geoscience.

Joint learning of variational representations and solvers for inverse problems with partially-observed data

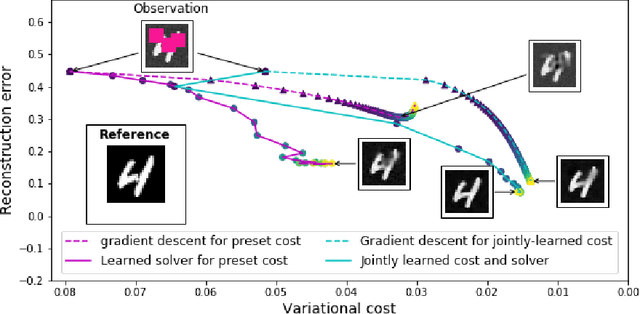
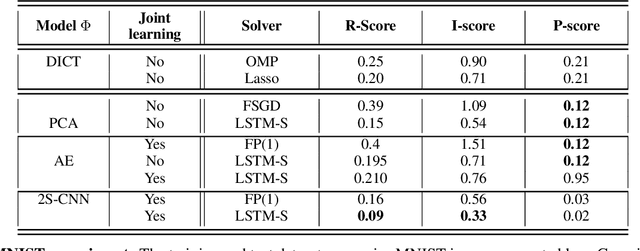
Designing appropriate variational regularization schemes is a crucial part of solving inverse problems, making them better-posed and guaranteeing that the solution of the associated optimization problem satisfies desirable properties. Recently, learning-based strategies have appeared to be very efficient for solving inverse problems, by learning direct inversion schemes or plug-and-play regularizers from available pairs of true states and observations. In this paper, we go a step further and design an end-to-end framework allowing to learn actual variational frameworks for inverse problems in such a supervised setting. The variational cost and the gradient-based solver are both stated as neural networks using automatic differentiation for the latter. We can jointly learn both components to minimize the data reconstruction error on the true states. This leads to a data-driven discovery of variational models. We consider an application to inverse problems with incomplete datasets (image inpainting and multivariate time series interpolation). We experimentally illustrate that this framework can lead to a significant gain in terms of reconstruction performance, including w.r.t. the direct minimization of the variational formulation derived from the known generative model.