Fiducial Matching: Differentially Private Inference for Categorical Data

The task of statistical inference, which includes the building of confidence intervals and tests for parameters and effects of interest to a researcher, is still an open area of investigation in a differentially private (DP) setting. Indeed, in addition to the randomness due to data sampling, DP delivers another source of randomness consisting of the noise added to protect an individual's data from being disclosed to a potential attacker. As a result of this convolution of noises, in many cases it is too complicated to determine the stochastic behavior of the statistics and parameters resulting from a DP procedure. In this work, we contribute to this line of investigation by employing a simulation-based matching approach, solved through tools from the fiducial framework, which aims to replicate the data generation pipeline (including the DP step) and retrieve an approximate distribution of the estimates resulting from this pipeline. For this purpose, we focus on the analysis of categorical (nominal) data that is common in national surveys, for which sensitivity is naturally defined, and on additive privacy mechanisms. We prove the validity of the proposed approach in terms of coverage and highlight its good computational and statistical performance for different inferential tasks in simulated and applied data settings.

Inference for Large Scale Regression Models with Dependent Errors

The exponential growth in data sizes and storage costs has brought considerable challenges to the data science community, requiring solutions to run learning methods on such data. While machine learning has scaled to achieve predictive accuracy in big data settings, statistical inference and uncertainty quantification tools are still lagging. Priority scientific fields collect vast data to understand phenomena typically studied with statistical methods like regression. In this setting, regression parameter estimation can benefit from efficient computational procedures, but the main challenge lies in computing error process parameters with complex covariance structures. Identifying and estimating these structures is essential for inference and often used for uncertainty quantification in machine learning with Gaussian Processes. However, estimating these structures becomes burdensome as data scales, requiring approximations that compromise the reliability of outputs. These approximations are even more unreliable when complexities like long-range dependencies or missing data are present. This work defines and proves the statistical properties of the Generalized Method of Wavelet Moments with Exogenous variables (GMWMX), a highly scalable, stable, and statistically valid method for estimating and delivering inference for linear models using stochastic processes in the presence of data complexities like latent dependence structures and missing data. Applied examples from Earth Sciences and extensive simulations highlight the advantages of the GMWMX.

Multi-Signal Approaches for Repeated Sampling Schemes in Inertial Sensor Calibration

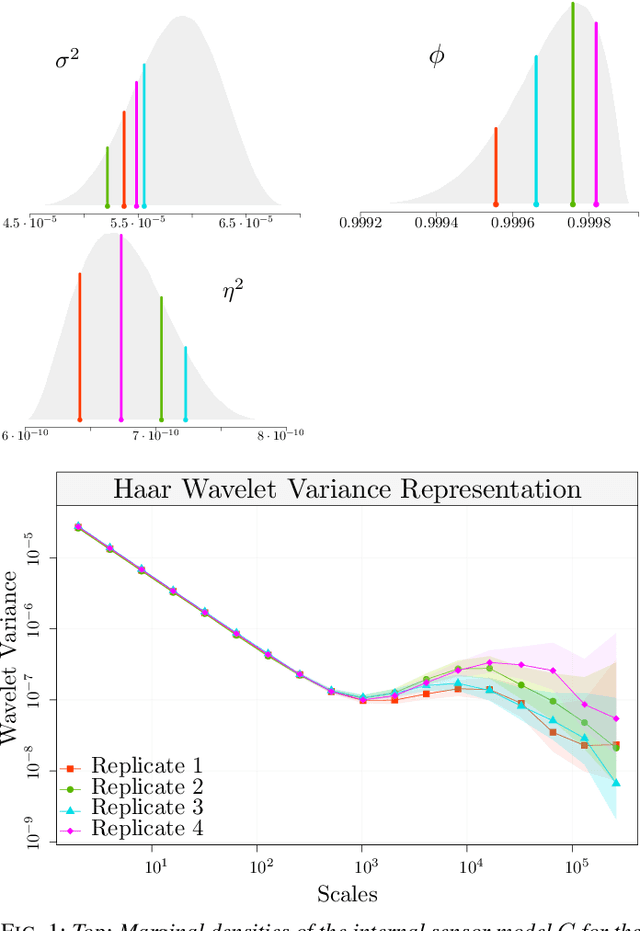
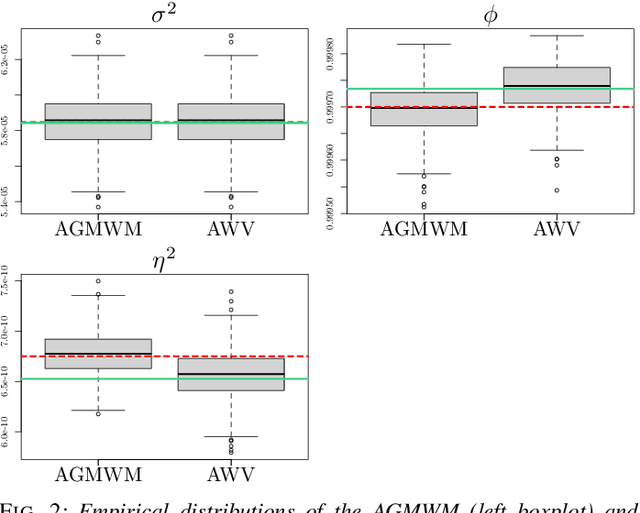
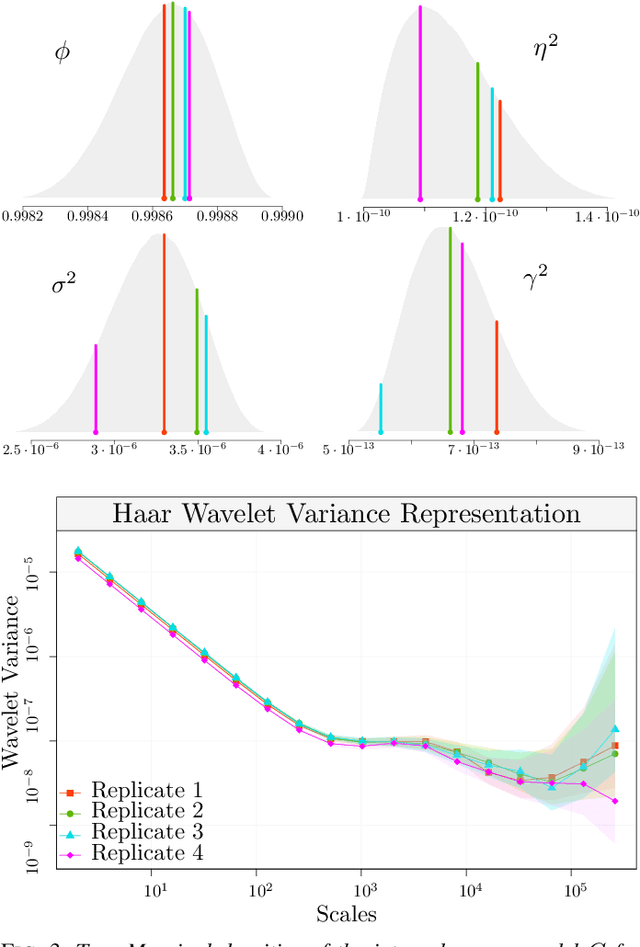
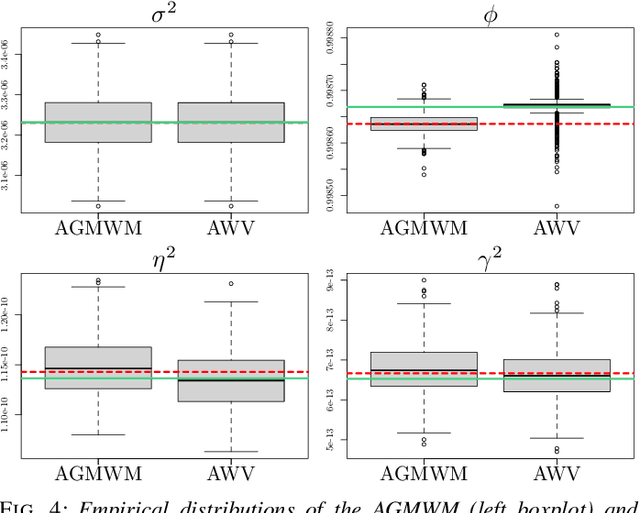
The task of inertial sensor calibration has become increasingly important due to the growing use of low-cost inertial measurement units which are however characterized by measurement errors. Being widely employed in a variety of mass-market applications, there is considerable focus on compensating for these errors by taking into account the deterministic and stochastic factors that characterize them. In this paper, we focus on the stochastic part of the error signal where it is customary to record the latter and use the observed error signal to identify and estimate the stochastic models, often complex in nature, that underlie this process. However, it is often the case that these error signals are observed through a series of replicates for the same inertial sensor and equally often that these replicates have the same model structure but their parameters appear different between replicates. This phenomenon has not been taken into account by current stochastic calibration procedures which therefore can be conditioned by flawed parameter estimation. For this reason, this paper aims at studying different approaches for this problem and studying their properties to take into account parameter variation between replicates thereby improving measurement precision and navigation uncertainty quantification in the long run.

SWAG: A Wrapper Method for Sparse Learning

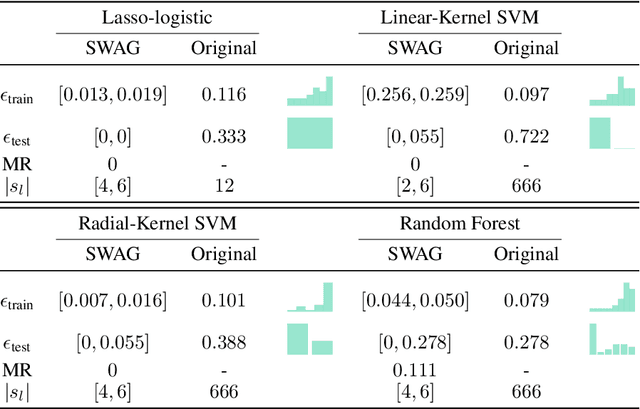
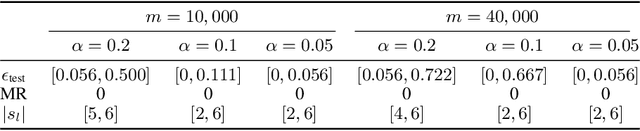
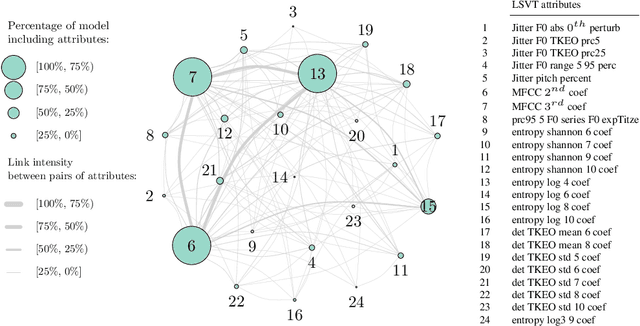
Predictive power has always been the main research focus of learning algorithms. While the general approach for these algorithms is to consider all possible attributes in a dataset to best predict the response of interest, an important branch of research is focused on sparse learning. Indeed, in many practical settings we believe that only an extremely small combination of different attributes affect the response. However even sparse-learning methods can still preserve a high number of attributes in high-dimensional settings and possibly deliver inconsistent prediction performance. The latter methods can also be hard to interpret for researchers and practitioners, a problem which is even more relevant for the ``black-box''-type mechanisms of many learning approaches. Finally, there is often a problem of replicability since not all data-collection procedures measure (or observe) the same attributes and therefore cannot make use of proposed learners for testing purposes. To address all the previous issues, we propose to study a procedure that combines screening and wrapper methods and aims to find a library of extremely low-dimensional attribute combinations (with consequent low data collection and storage costs) in order to (i) match or improve the predictive performance of any particular learning method which uses all attributes as an input (including sparse learners); (ii) provide a low-dimensional network of attributes easily interpretable by researchers and practitioners; and (iii) increase the potential replicability of results due to a diversity of attribute combinations defining strong learners with equivalent predictive power. We call this algorithm ``Sparse Wrapper AlGorithm'' (SWAG).