Normalized Radon Cumulative Distribution Transforms for Invariance and Robustness in Optimal Transport Based Image Classification

The Radon cumulative distribution transform (R-CDT), is an easy-to-compute feature extractor that facilitates image classification tasks especially in the small data regime. It is closely related to the sliced Wasserstein distance and provably guaranties the linear separability of image classes that emerge from translations or scalings. In many real-world applications, like the recognition of watermarks in filigranology, however, the data is subject to general affine transformations originating from the measurement process. To overcome this issue, we recently introduced the so-called max-normalized R-CDT that only requires elementary operations and guaranties the separability under arbitrary affine transformations. The aim of this paper is to continue our study of the max-normalized R-CDT especially with respect to its robustness against non-affine image deformations. Our sensitivity analysis shows that its separability properties are stable provided the Wasserstein-infinity distance between the samples can be controlled. Since the Wasserstein-infinity distance only allows small local image deformations, we moreover introduce a mean-normalized version of the R-CDT. In this case, robustness relates to the Wasserstein-2 distance and also covers image deformations caused by impulsive noise for instance. Our theoretical results are supported by numerical experiments showing the effectiveness of our novel feature extractors as well as their robustness against local non-affine deformations and impulsive noise.

Slicing the Gaussian Mixture Wasserstein Distance

Gaussian mixture models (GMMs) are widely used in machine learning for tasks such as clustering, classification, image reconstruction, and generative modeling. A key challenge in working with GMMs is defining a computationally efficient and geometrically meaningful metric. The mixture Wasserstein (MW) distance adapts the Wasserstein metric to GMMs and has been applied in various domains, including domain adaptation, dataset comparison, and reinforcement learning. However, its high computational cost -- arising from repeated Wasserstein distance computations involving matrix square root estimations and an expensive linear program -- limits its scalability to high-dimensional and large-scale problems. To address this, we propose multiple novel slicing-based approximations to the MW distance that significantly reduce computational complexity while preserving key optimal transport properties. From a theoretical viewpoint, we establish several weak and strong equivalences between the introduced metrics, and show the relations to the original MW distance and the well-established sliced Wasserstein distance. Furthermore, we validate the effectiveness of our approach through numerical experiments, demonstrating computational efficiency and applications in clustering, perceptual image comparison, and GMM minimization

Joint Metric Space Embedding by Unbalanced OT with Gromov-Wasserstein Marginal Penalization

We propose a new approach for unsupervised alignment of heterogeneous datasets, which maps data from two different domains without any known correspondences to a common metric space. Our method is based on an unbalanced optimal transport problem with Gromov-Wasserstein marginal penalization. It can be seen as a counterpart to the recently introduced joint multidimensional scaling method. We prove that there exists a minimizer of our functional and that for penalization parameters going to infinity, the corresponding sequence of minimizers converges to a minimizer of the so-called embedded Wasserstein distance. Our model can be reformulated as a quadratic, multi-marginal, unbalanced optimal transport problem, for which a bi-convex relaxation admits a numerical solver via block-coordinate descent. We provide numerical examples for joint embeddings in Euclidean as well as non-Euclidean spaces.

Wasserstein Gradient Flows of MMD Functionals with Distance Kernel and Cauchy Problems on Quantile Functions

We give a comprehensive description of Wasserstein gradient flows of maximum mean discrepancy (MMD) functionals $\mathcal F_\nu := \text{MMD}_K^2(\cdot, \nu)$ towards given target measures $\nu$ on the real line, where we focus on the negative distance kernel $K(x,y) := -|x-y|$. In one dimension, the Wasserstein-2 space can be isometrically embedded into the cone $\mathcal C(0,1) \subset L_2(0,1)$ of quantile functions leading to a characterization of Wasserstein gradient flows via the solution of an associated Cauchy problem on $L_2(0,1)$. Based on the construction of an appropriate counterpart of $\mathcal F_\nu$ on $L_2(0,1)$ and its subdifferential, we provide a solution of the Cauchy problem. For discrete target measures $\nu$, this results in a piecewise linear solution formula. We prove invariance and smoothing properties of the flow on subsets of $\mathcal C(0,1)$. For certain $\mathcal F_\nu$-flows this implies that initial point measures instantly become absolutely continuous, and stay so over time. Finally, we illustrate the behavior of the flow by various numerical examples using an implicit Euler scheme and demonstrate differences to the explicit Euler scheme, which is easier to compute, but comes with limited convergence guarantees.

Posterior Sampling Based on Gradient Flows of the MMD with Negative Distance Kernel

We propose conditional flows of the maximum mean discrepancy (MMD) with the negative distance kernel for posterior sampling and conditional generative modeling. This MMD, which is also known as energy distance, has several advantageous properties like efficient computation via slicing and sorting. We approximate the joint distribution of the ground truth and the observations using discrete Wasserstein gradient flows and establish an error bound for the posterior distributions. Further, we prove that our particle flow is indeed a Wasserstein gradient flow of an appropriate functional. The power of our method is demonstrated by numerical examples including conditional image generation and inverse problems like superresolution, inpainting and computed tomography in low-dose and limited-angle settings.

Total variation-based phase retrieval for diffraction tomography

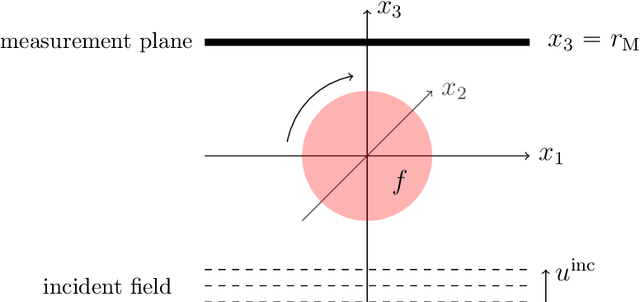
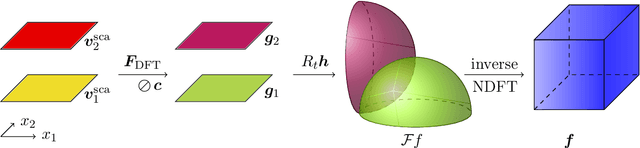
In optical diffraction tomography (ODT), the three-dimensional scattering potential of a microscopic object rotating around its center is recovered by a series of illuminations with coherent light. Reconstruction algorithms such as the filtered backpropagation require knowledge of the complex-valued wave at the measurement plane, whereas often only intensities, i.e., phaseless measurements, are available in practice. We propose a new reconstruction approach for ODT with unknown phase information based on three key ingredients. First, the light propagation is modeled using Born's approximation enabling us to use the Fourier diffraction theorem. Second, we stabilize the inversion of the non-uniform discrete Fourier transform via total variation regularization utilizing a primal-dual iteration, which also yields a novel numerical inversion formula for ODT with known phase. The third ingredient is a hybrid input-output scheme. We achieved convincing numerical results, which indicate that ODT with phaseless data is possible. The so-obtained 2D and 3D reconstructions are even comparable to the ones with known phase.