Towards understanding Accelerated Stein Variational Gradient Flow -- Analysis of Generalized Bilinear Kernels for Gaussian target distributions

Stein variational gradient descent (SVGD) is a kernel-based and non-parametric particle method for sampling from a target distribution, such as in Bayesian inference and other machine learning tasks. Different from other particle methods, SVGD does not require estimating the score, which is the gradient of the log-density. However, in practice, SVGD can be slow compared to score-estimation-based sampling algorithms. To design a fast and efficient high-dimensional sampling algorithm with the advantages of SVGD, we introduce accelerated SVGD (ASVGD), based on an accelerated gradient flow in a metric space of probability densities following Nesterov's method. We then derive a momentum-based discrete-time sampling algorithm, which evolves a set of particles deterministically. To stabilize the particles' position update, we also include a Wasserstein metric regularization. This paper extends the conference version \cite{SL2025}. For the bilinear kernel and Gaussian target distributions, we study the kernel parameter and damping parameters with an optimal convergence rate of the proposed dynamics. This is achieved by analyzing the linearized accelerated gradient flows at the equilibrium. Interestingly, the optimal parameter is a constant, which does not depend on the covariance of the target distribution. For the generalized kernel functions, such as the Gaussian kernel, numerical examples with varied target distributions demonstrate the effectiveness of ASVGD compared to SVGD and other popular sampling methods. Furthermore, we show that in the setting of Bayesian neural networks, ASVGD outperforms SVGD significantly in terms of log-likelihood and total iteration times.

Accelerated Stein Variational Gradient Flow

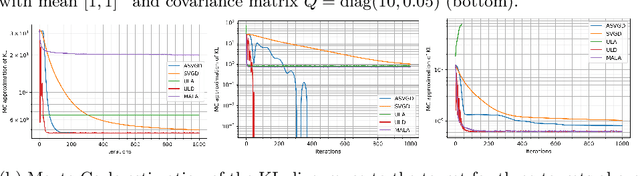
Stein variational gradient descent (SVGD) is a kernel-based particle method for sampling from a target distribution, e.g., in generative modeling and Bayesian inference. SVGD does not require estimating the gradient of the log-density, which is called score estimation. In practice, SVGD can be slow compared to score-estimation based sampling algorithms. To design fast and efficient high-dimensional sampling algorithms, we introduce ASVGD, an accelerated SVGD, based on an accelerated gradient flow in a metric space of probability densities following Nesterov's method. We then derive a momentum-based discrete-time sampling algorithm, which evolves a set of particles deterministically. To stabilize the particles' momentum update, we also study a Wasserstein metric regularization. For the generalized bilinear kernel and the Gaussian kernel, toy numerical examples with varied target distributions demonstrate the effectiveness of ASVGD compared to SVGD and other popular sampling methods.

Wasserstein Gradient Flows of MMD Functionals with Distance Kernel and Cauchy Problems on Quantile Functions

We give a comprehensive description of Wasserstein gradient flows of maximum mean discrepancy (MMD) functionals $\mathcal F_\nu := \text{MMD}_K^2(\cdot, \nu)$ towards given target measures $\nu$ on the real line, where we focus on the negative distance kernel $K(x,y) := -|x-y|$. In one dimension, the Wasserstein-2 space can be isometrically embedded into the cone $\mathcal C(0,1) \subset L_2(0,1)$ of quantile functions leading to a characterization of Wasserstein gradient flows via the solution of an associated Cauchy problem on $L_2(0,1)$. Based on the construction of an appropriate counterpart of $\mathcal F_\nu$ on $L_2(0,1)$ and its subdifferential, we provide a solution of the Cauchy problem. For discrete target measures $\nu$, this results in a piecewise linear solution formula. We prove invariance and smoothing properties of the flow on subsets of $\mathcal C(0,1)$. For certain $\mathcal F_\nu$-flows this implies that initial point measures instantly become absolutely continuous, and stay so over time. Finally, we illustrate the behavior of the flow by various numerical examples using an implicit Euler scheme and demonstrate differences to the explicit Euler scheme, which is easier to compute, but comes with limited convergence guarantees.

Wasserstein Gradient Flows for Moreau Envelopes of f-Divergences in Reproducing Kernel Hilbert Spaces

Most commonly used $f$-divergences of measures, e.g., the Kullback-Leibler divergence, are subject to limitations regarding the support of the involved measures. A remedy consists of regularizing the $f$-divergence by a squared maximum mean discrepancy (MMD) associated with a characteristic kernel $K$. In this paper, we use the so-called kernel mean embedding to show that the corresponding regularization can be rewritten as the Moreau envelope of some function in the reproducing kernel Hilbert space associated with $K$. Then, we exploit well-known results on Moreau envelopes in Hilbert spaces to prove properties of the MMD-regularized $f$-divergences and, in particular, their gradients. Subsequently, we use our findings to analyze Wasserstein gradient flows of MMD-regularized $f$-divergences. Finally, we consider Wasserstein gradient flows starting from empirical measures and provide proof-of-the-concept numerical examples with Tsallis-$\alpha$ divergences.