AFABench: A Generic Framework for Benchmarking Active Feature Acquisition

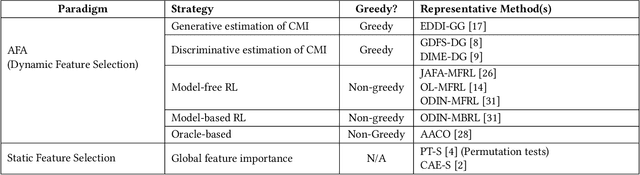
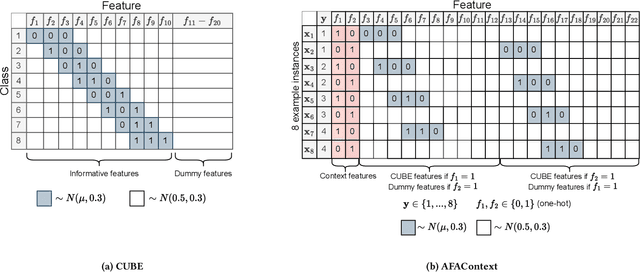
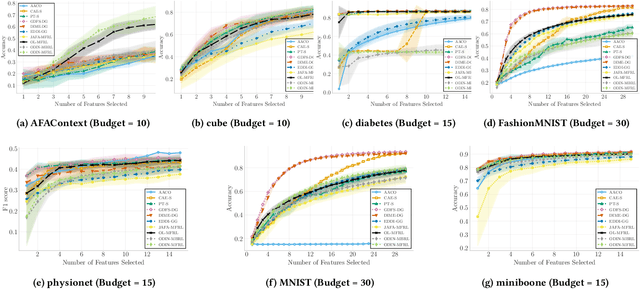
In many real-world scenarios, acquiring all features of a data instance can be expensive or impractical due to monetary cost, latency, or privacy concerns. Active Feature Acquisition (AFA) addresses this challenge by dynamically selecting a subset of informative features for each data instance, trading predictive performance against acquisition cost. While numerous methods have been proposed for AFA, ranging from greedy information-theoretic strategies to non-myopic reinforcement learning approaches, fair and systematic evaluation of these methods has been hindered by the lack of standardized benchmarks. In this paper, we introduce AFABench, the first benchmark framework for AFA. Our benchmark includes a diverse set of synthetic and real-world datasets, supports a wide range of acquisition policies, and provides a modular design that enables easy integration of new methods and tasks. We implement and evaluate representative algorithms from all major categories, including static, greedy, and reinforcement learning-based approaches. To test the lookahead capabilities of AFA policies, we introduce a novel synthetic dataset, AFAContext, designed to expose the limitations of greedy selection. Our results highlight key trade-offs between different AFA strategies and provide actionable insights for future research. The benchmark code is available at: https://github.com/Linusaronsson/AFA-Benchmark.

ClaudesLens: Uncertainty Quantification in Computer Vision Models

In a world where more decisions are made using artificial intelligence, it is of utmost importance to ensure these decisions are well-grounded. Neural networks are the modern building blocks for artificial intelligence. Modern neural network-based computer vision models are often used for object classification tasks. Correctly classifying objects with \textit{certainty} has become of great importance in recent times. However, quantifying the inherent \textit{uncertainty} of the output from neural networks is a challenging task. Here we show a possible method to quantify and evaluate the uncertainty of the output of different computer vision models based on Shannon entropy. By adding perturbation of different levels, on different parts, ranging from the input to the parameters of the network, one introduces entropy to the system. By quantifying and evaluating the perturbed models on the proposed PI and PSI metrics, we can conclude that our theoretical framework can grant insight into the uncertainty of predictions of computer vision models. We believe that this theoretical framework can be applied to different applications for neural networks. We believe that Shannon entropy may eventually have a bigger role in the SOTA (State-of-the-art) methods to quantify uncertainty in artificial intelligence. One day we might be able to apply Shannon entropy to our neural systems.