Personalized Bayesian Federated Learning with Wasserstein Barycenter Aggregation

Personalized Bayesian federated learning (PBFL) handles non-i.i.d. client data and quantifies uncertainty by combining personalization with Bayesian inference. However, existing PBFL methods face two limitations: restrictive parametric assumptions in client posterior inference and naive parameter averaging for server aggregation. To overcome these issues, we propose FedWBA, a novel PBFL method that enhances both local inference and global aggregation. At the client level, we use particle-based variational inference for nonparametric posterior representation. At the server level, we introduce particle-based Wasserstein barycenter aggregation, offering a more geometrically meaningful approach. Theoretically, we provide local and global convergence guarantees for FedWBA. Locally, we prove a KL divergence decrease lower bound per iteration for variational inference convergence. Globally, we show that the Wasserstein barycenter converges to the true parameter as the client data size increases. Empirically, experiments show that FedWBA outperforms baselines in prediction accuracy, uncertainty calibration, and convergence rate, with ablation studies confirming its robustness.

Influence Maximization in Hypergraphs Using A Genetic Algorithm with New Initialization and Evaluation Methods

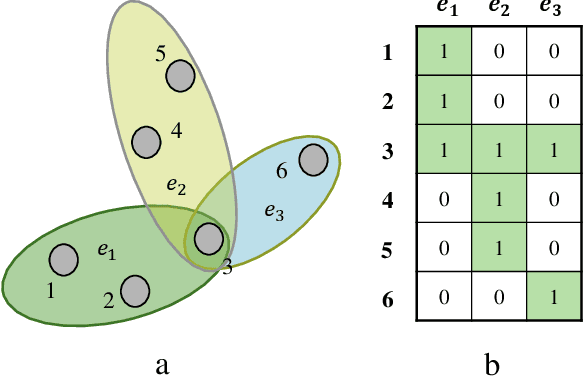
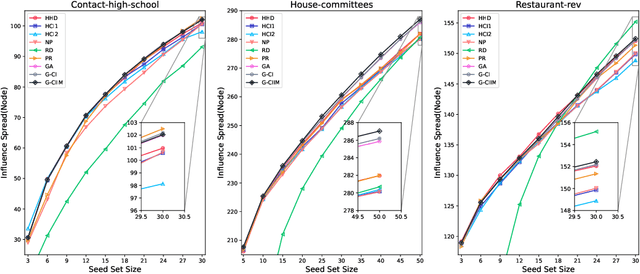
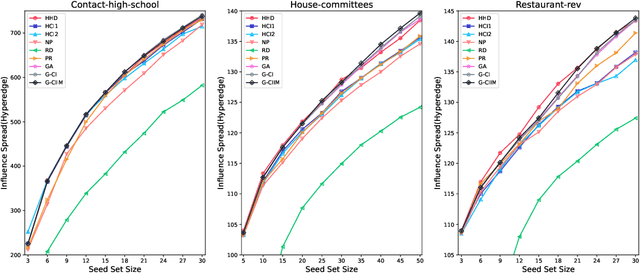
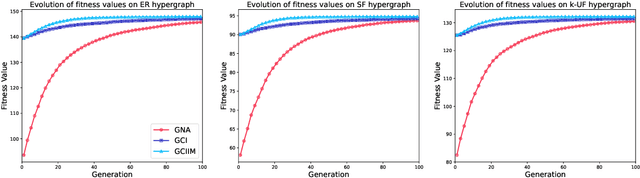
Influence maximization (IM) is a crucial optimization task related to analyzing complex networks in the real world, such as social networks, disease propagation networks, and marketing networks. Publications to date about the IM problem focus mainly on graphs, which fail to capture high-order interaction relationships from the real world. Therefore, the use of hypergraphs for addressing the IM problem has been receiving increasing attention. However, identifying the most influential nodes in hypergraphs remains challenging, mainly because nodes and hyperedges are often strongly coupled and correlated. In this paper, to effectively identify the most influential nodes, we first propose a novel hypergraph-independent cascade model that integrates the influences of both node and hyperedge failures. Afterward, we introduce genetic algorithms (GA) to identify the most influential nodes that leverage hypergraph collective influences. In the GA-based method, the hypergraph collective influence is effectively used to initialize the population, thereby enhancing the quality of initial candidate solutions. The designed fitness function considers the joint influences of both nodes and hyperedges. This ensures the optimal set of nodes with the best influence on both nodes and hyperedges to be evaluated accurately. Moreover, a new mutation operator is designed by introducing factors, i.e., the collective influence and overlapping effects of nodes in hypergraphs, to breed high-quality offspring. In the experiments, several simulations on both synthetic and real hypergraphs have been conducted, and the results demonstrate that the proposed method outperforms the compared methods.