Training with Quantization Noise for Extreme Model Compression

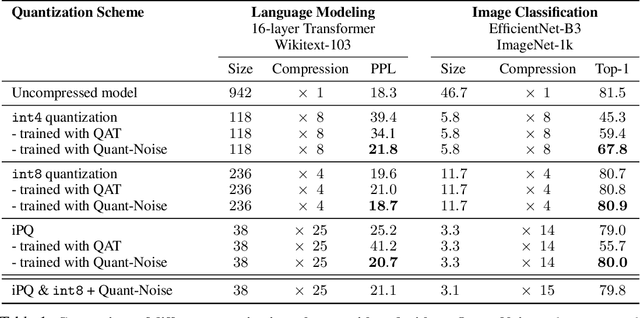
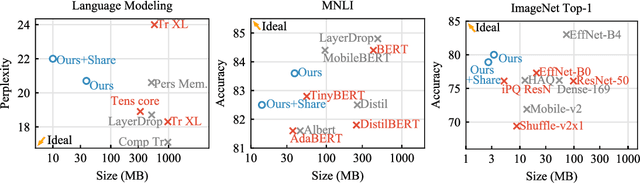
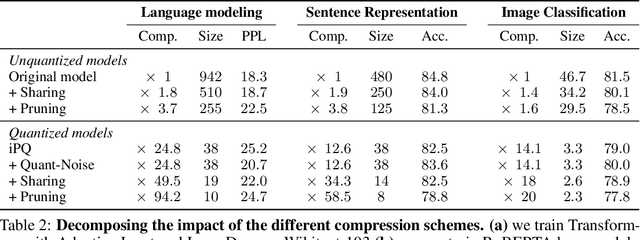
We tackle the problem of producing compact models, maximizing their accuracy for a given model size. A standard solution is to train networks with Quantization Aware Training, where the weights are quantized during training and the gradients approximated with the Straight-Through Estimator. In this paper, we extend this approach to work beyond int8 fixed-point quantization with extreme compression methods where the approximations introduced by STE are severe, such as Product Quantization. Our proposal is to only quantize a different random subset of weights during each forward, allowing for unbiased gradients to flow through the other weights. Controlling the amount of noise and its form allows for extreme compression rates while maintaining the performance of the original model. As a result we establish new state-of-the-art compromises between accuracy and model size both in natural language processing and image classification. For example, applying our method to state-of-the-art Transformer and ConvNet architectures, we can achieve 82.5% accuracy on MNLI by compressing RoBERTa to 14MB and 80.0 top-1 accuracy on ImageNet by compressing an EfficientNet-B3 to 3.3MB.

Compressive Spectral Clustering

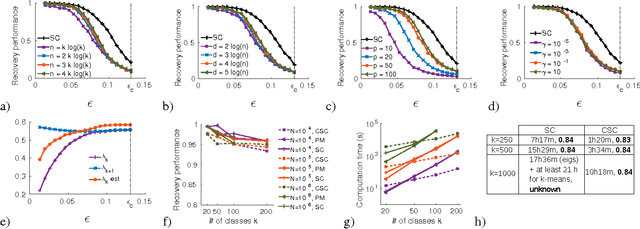
Spectral clustering has become a popular technique due to its high performance in many contexts. It comprises three main steps: create a similarity graph between N objects to cluster, compute the first k eigenvectors of its Laplacian matrix to define a feature vector for each object, and run k-means on these features to separate objects into k classes. Each of these three steps becomes computationally intensive for large N and/or k. We propose to speed up the last two steps based on recent results in the emerging field of graph signal processing: graph filtering of random signals, and random sampling of bandlimited graph signals. We prove that our method, with a gain in computation time that can reach several orders of magnitude, is in fact an approximation of spectral clustering, for which we are able to control the error. We test the performance of our method on artificial and real-world network data.

Constrained Overcomplete Analysis Operator Learning for Cosparse Signal Modelling

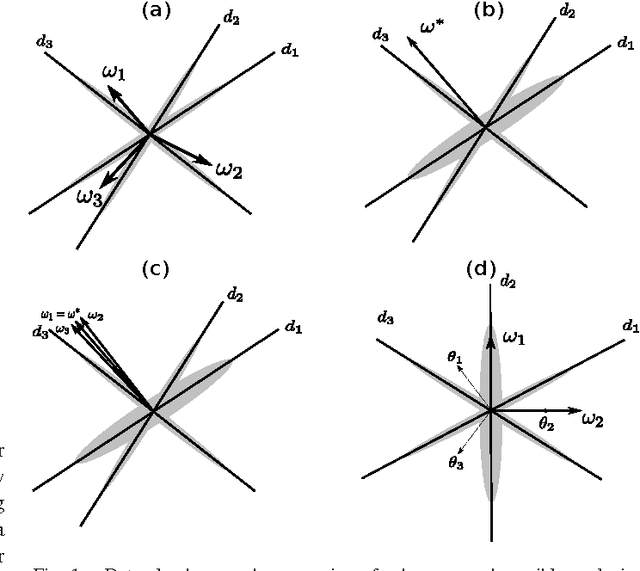
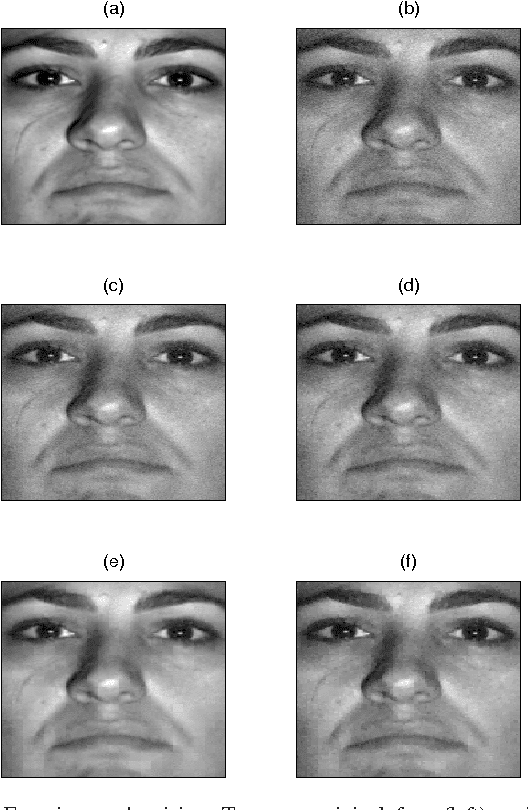
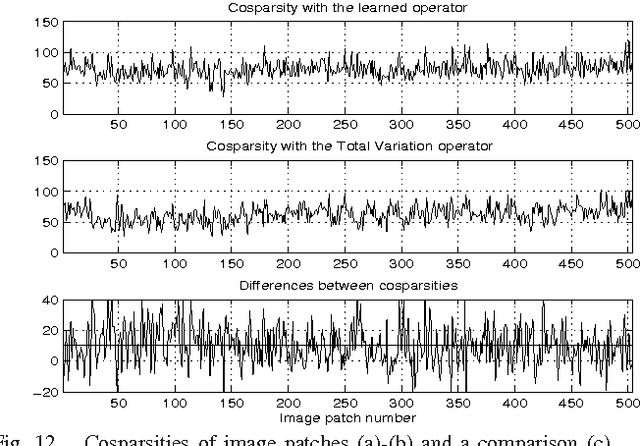
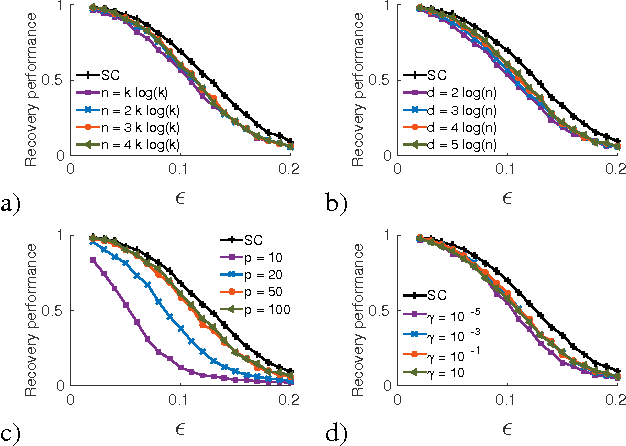
We consider the problem of learning a low-dimensional signal model from a collection of training samples. The mainstream approach would be to learn an overcomplete dictionary to provide good approximations of the training samples using sparse synthesis coefficients. This famous sparse model has a less well known counterpart, in analysis form, called the cosparse analysis model. In this new model, signals are characterised by their parsimony in a transformed domain using an overcomplete (linear) analysis operator. We propose to learn an analysis operator from a training corpus using a constrained optimisation framework based on L1 optimisation. The reason for introducing a constraint in the optimisation framework is to exclude trivial solutions. Although there is no final answer here for which constraint is the most relevant constraint, we investigate some conventional constraints in the model adaptation field and use the uniformly normalised tight frame (UNTF) for this purpose. We then derive a practical learning algorithm, based on projected subgradients and Douglas-Rachford splitting technique, and demonstrate its ability to robustly recover a ground truth analysis operator, when provided with a clean training set, of sufficient size. We also find an analysis operator for images, using some noisy cosparse signals, which is indeed a more realistic experiment. As the derived optimisation problem is not a convex program, we often find a local minimum using such variational methods. Some local optimality conditions are derived for two different settings, providing preliminary theoretical support for the well-posedness of the learning problem under appropriate conditions.

Dictionary Identification - Sparse Matrix-Factorisation via $\ell_1$-Minimisation

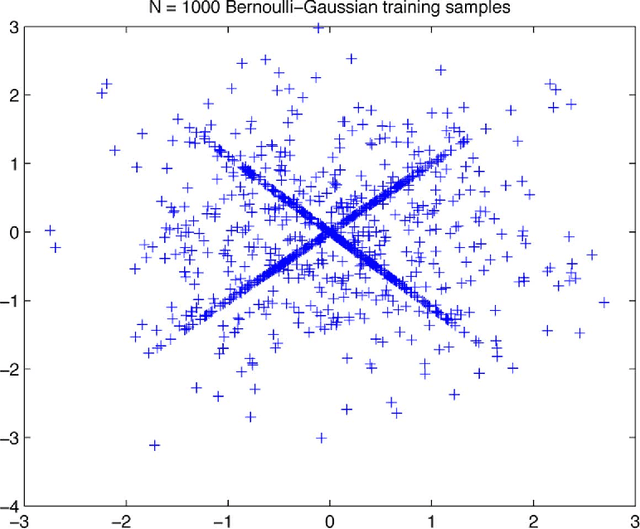
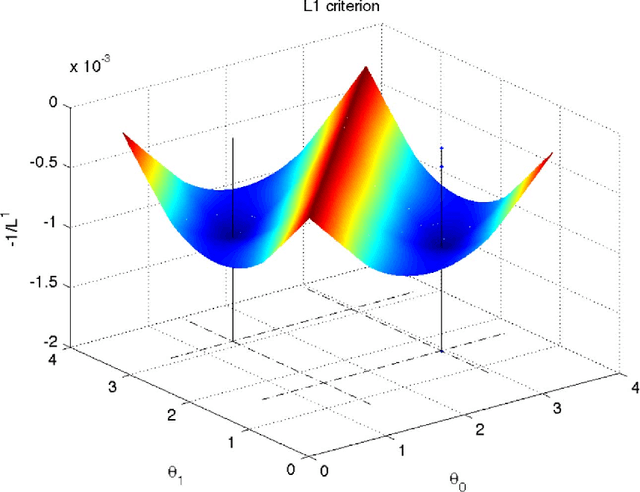
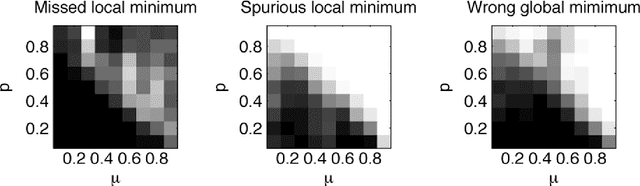
This article treats the problem of learning a dictionary providing sparse representations for a given signal class, via $\ell_1$-minimisation. The problem can also be seen as factorising a $\ddim \times \nsig$ matrix $Y=(y_1 >... y_\nsig), y_n\in \R^\ddim$ of training signals into a $\ddim \times \natoms$ dictionary matrix $\dico$ and a $\natoms \times \nsig$ coefficient matrix $\X=(x_1... x_\nsig), x_n \in \R^\natoms$, which is sparse. The exact question studied here is when a dictionary coefficient pair $(\dico,\X)$ can be recovered as local minimum of a (nonconvex) $\ell_1$-criterion with input $Y=\dico \X$. First, for general dictionaries and coefficient matrices, algebraic conditions ensuring local identifiability are derived, which are then specialised to the case when the dictionary is a basis. Finally, assuming a random Bernoulli-Gaussian sparse model on the coefficient matrix, it is shown that sufficiently incoherent bases are locally identifiable with high probability. The perhaps surprising result is that the typically sufficient number of training samples $\nsig$ grows up to a logarithmic factor only linearly with the signal dimension, i.e. $\nsig \approx C \natoms \log \natoms$, in contrast to previous approaches requiring combinatorially many samples.

Under-determined reverberant audio source separation using a full-rank spatial covariance model

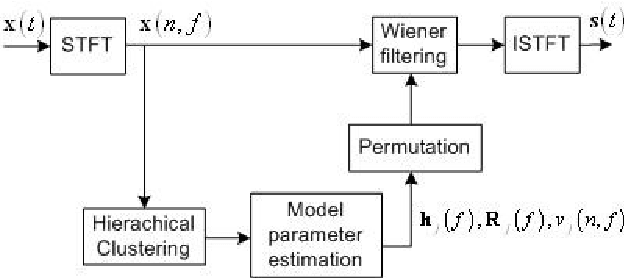
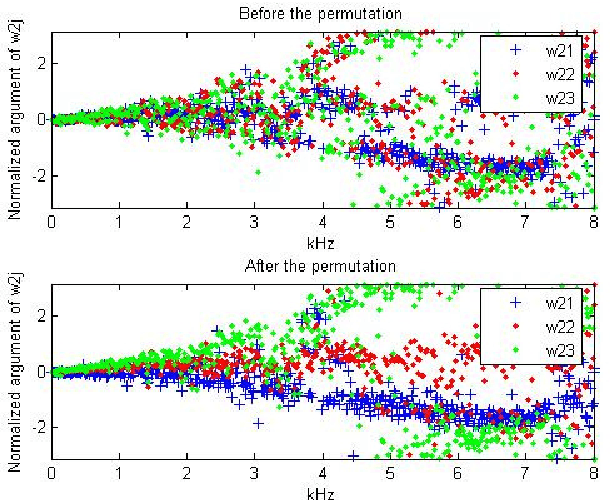
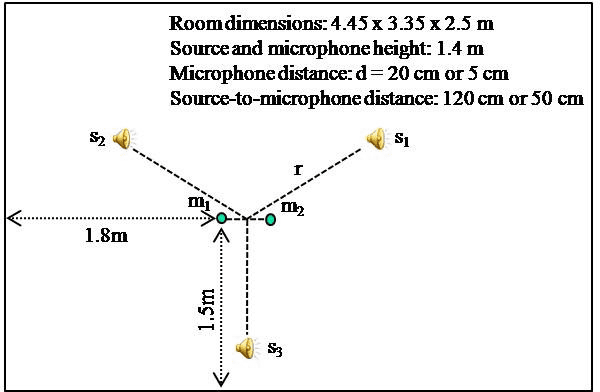
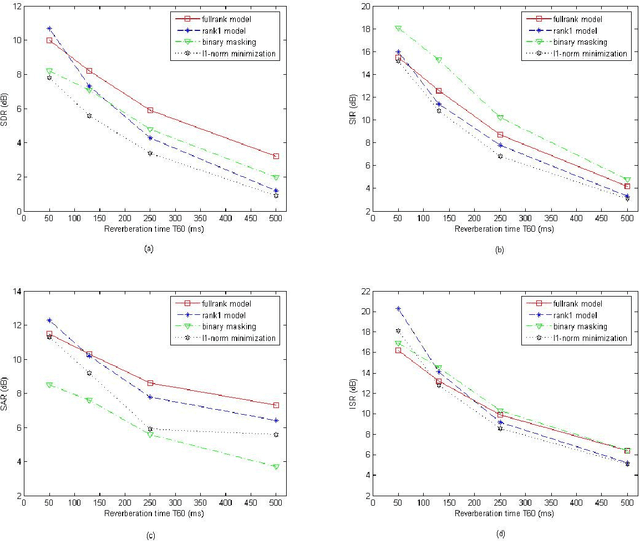
This article addresses the modeling of reverberant recording environments in the context of under-determined convolutive blind source separation. We model the contribution of each source to all mixture channels in the time-frequency domain as a zero-mean Gaussian random variable whose covariance encodes the spatial characteristics of the source. We then consider four specific covariance models, including a full-rank unconstrained model. We derive a family of iterative expectationmaximization (EM) algorithms to estimate the parameters of each model and propose suitable procedures to initialize the parameters and to align the order of the estimated sources across all frequency bins based on their estimated directions of arrival (DOA). Experimental results over reverberant synthetic mixtures and live recordings of speech data show the effectiveness of the proposed approach.