Convergence of Message Passing Graph Neural Networks with Generic Aggregation On Large Random Graphs

We study the convergence of message passing graph neural networks on random graph models to their continuous counterpart as the number of nodes tends to infinity. Until now, this convergence was only known for architectures with aggregation functions in the form of degree-normalized means. We extend such results to a very large class of aggregation functions, that encompasses all classically used message passing graph neural networks, such as attention-based mesage passing or max convolutional message passing on top of (degree-normalized) convolutional message passing. Under mild assumptions, we give non asymptotic bounds with high probability to quantify this convergence. Our main result is based on the McDiarmid inequality. Interestingly, we treat the case where the aggregation is a coordinate-wise maximum separately, at it necessitates a very different proof technique and yields a qualitatively different convergence rate.

A Faster Sampler for Discrete Determinantal Point Processes

Discrete Determinantal Point Processes (DPPs) have a wide array of potential applications for subsampling datasets. They are however held back in some cases by the high cost of sampling. In the worst-case scenario, the sampling cost scales as $O(n^3)$ where n is the number of elements of the ground set. A popular workaround to this prohibitive cost is to sample DPPs defined by low-rank kernels. In such cases, the cost of standard sampling algorithms scales as $O(np^2 + nm^2)$ where m is the (average) number of samples of the DPP (usually $m \ll n$) and p ($m \leq p \leq n$) the rank of the kernel used to define the DPP. The first term, $O(np^2)$, comes from a SVD-like step. We focus here on the second term of this cost, $O(nm^2)$, and show that it can be brought down to $O(nm + m^3 log m)$ without loss on the sampling's exactness. In practice, we observe extremely substantial speedups compared to the classical algorithm as soon as $n > 1, 000$. The algorithm described here is a close variant of the standard algorithm for sampling continuous DPPs, and uses rejection sampling. In the specific case of projection DPPs, we also show that any additional sample can be drawn in time $O(m^3 log m)$. Finally, an interesting by-product of the analysis is that a realisation from a DPP is typically contained in a subset of size $O(m log m)$ formed using leverage score i.i.d. sampling.

Variance Reduction for Inverse Trace Estimation via Random Spanning Forests

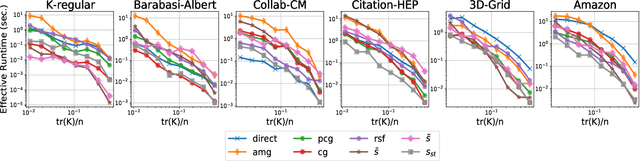
The trace $\tr(q(\ma{L} + q\ma{I})^{-1})$, where $\ma{L}$ is a symmetric diagonally dominant matrix, is the quantity of interest in some machine learning problems. However, its direct computation is impractical if the matrix size is large. State-of-the-art methods include Hutchinson's estimator combined with iterative solvers, as well as the estimator based on random spanning forests (a random process on graphs). In this work, we show two ways of improving the forest-based estimator via well-known variance reduction techniques, namely control variates and stratified sampling. Implementing these techniques is easy, and provides substantial variance reduction, yielding comparable or better performance relative to state-of-the-art algorithms.

Variance reduction in stochastic methods for large-scale regularised least-squares problems

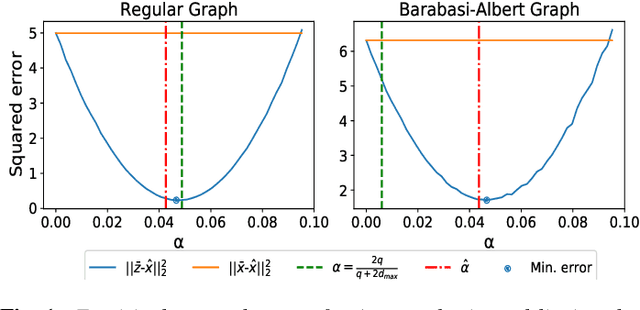
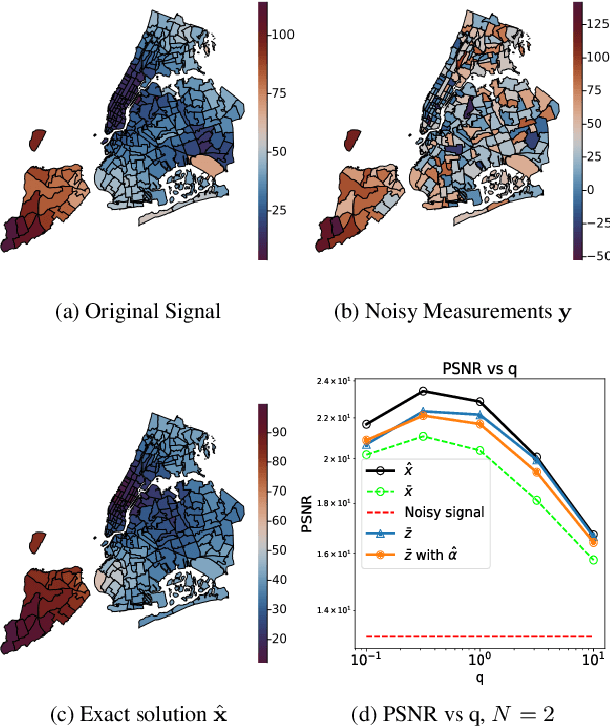
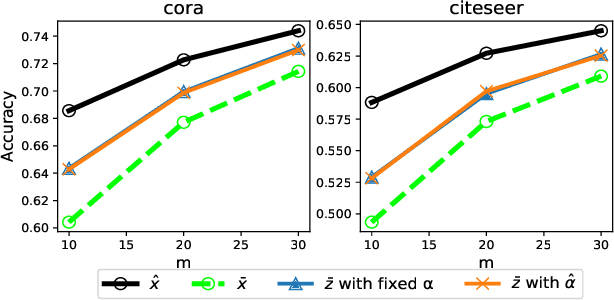
Large dimensional least-squares and regularised least-squares problems are expensive to solve. There exist many approximate techniques, some deterministic (like conjugate gradient), some stochastic (like stochastic gradient descent). Among the latter, a new class of techniques uses Determinantal Point Processes (DPPs) to produce unbiased estimators of the solution. In particular, they can be used to perform Tikhonov regularization on graphs using random spanning forests, a specific DPP. While the unbiasedness of these algorithms is attractive, their variance can be high. We show here that variance can be reduced by combining the stochastic estimator with a deterministic gradient-descent step, while keeping the property of unbiasedness. We apply this technique to Tikhonov regularization on graphs, where the reduction in variance is found to be substantial at very small extra cost.

Nishimori meets Bethe: a spectral method for node classification in sparse weighted graphs

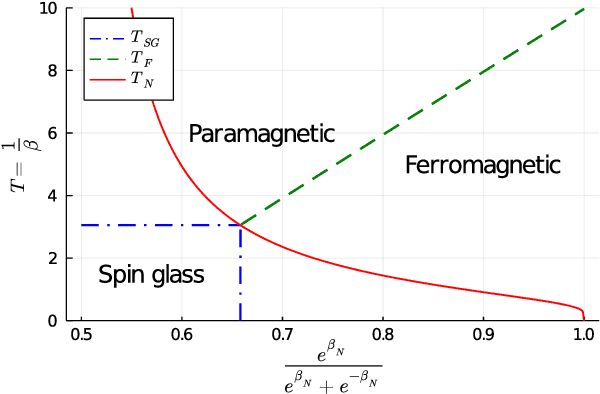
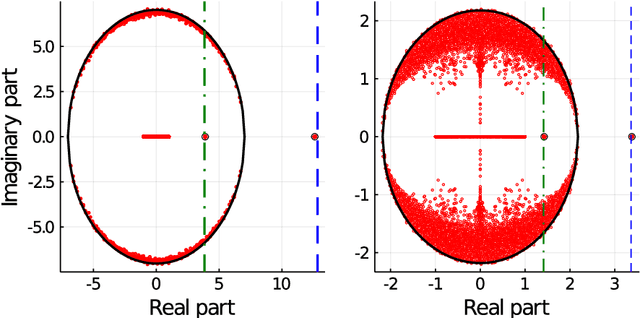
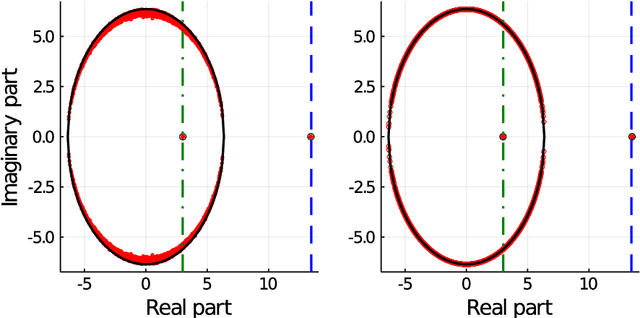
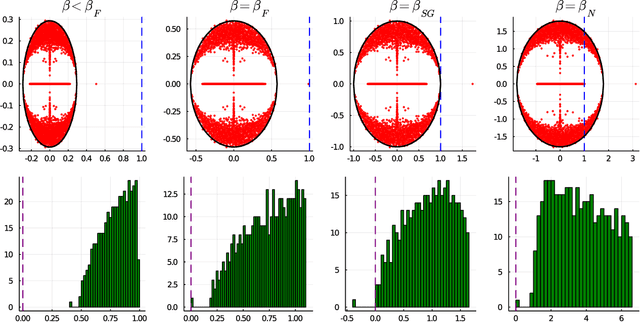
This article unveils a new relation between the Nishimori temperature parametrizing a distribution P and the Bethe free energy on random Erdos-Renyi graphs with edge weights distributed according to P. Estimating the Nishimori temperature being a task of major importance in Bayesian inference problems, as a practical corollary of this new relation, a numerical method is proposed to accurately estimate the Nishimori temperature from the eigenvalues of the Bethe Hessian matrix of the weighted graph. The algorithm, in turn, is used to propose a new spectral method for node classification in weighted (possibly sparse) graphs. The superiority of the method over competing state-of-the-art approaches is demonstrated both through theoretical arguments and real-world data experiments.

Fast Graph Kernel with Optical Random Features

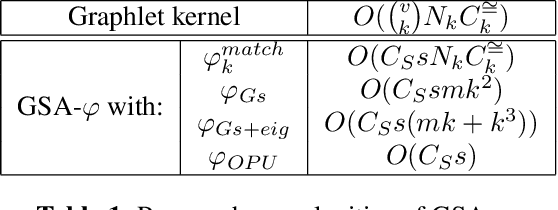
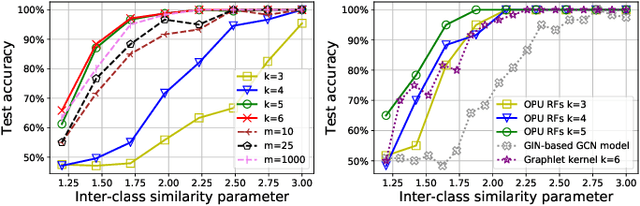
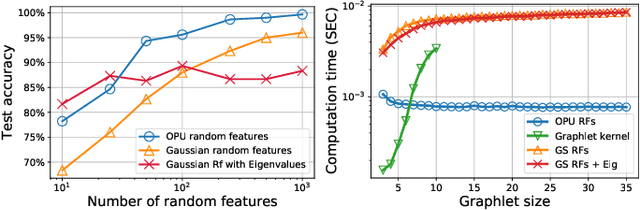
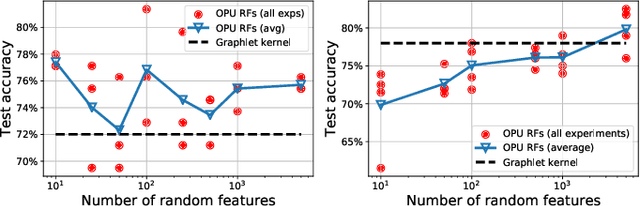
The graphlet kernel is a classical method in graph classification. It however suffers from a high computation cost due to the isomorphism test it includes. As a generic proxy, and in general at the cost of losing some information, this test can be efficiently replaced by a user-defined mapping that computes various graph characteristics. In this paper, we propose to leverage kernel random features within the graphlet framework, and establish a theoretical link with a mean kernel metric. If this method can still be prohibitively costly for usual random features, we then incorporate optical random features that can be computed in constant time. Experiments show that the resulting algorithm is orders of magnitude faster that the graphlet kernel for the same, or better, accuracy.

Community detection in sparse time-evolving graphs with a dynamical Bethe-Hessian

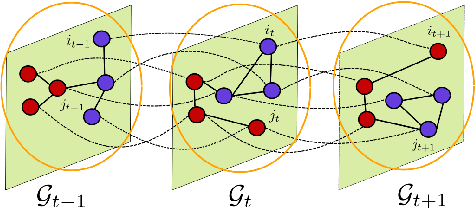
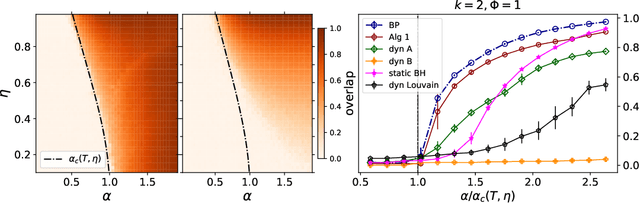
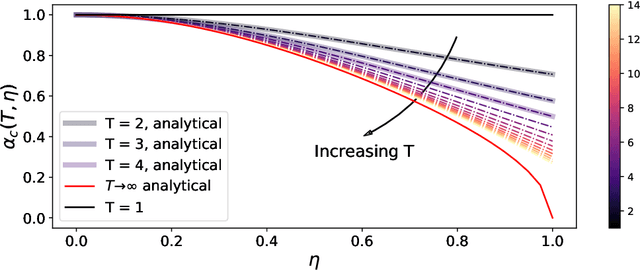
This article considers the problem of community detection in sparse dynamical graphs in which the community structure evolves over time. A fast spectral algorithm based on an extension of the Bethe-Hessian matrix is proposed, which benefits from the positive correlation in the class labels and in their temporal evolution and is designed to be applicable to any dynamical graph with a community structure. Under the dynamical degree-corrected stochastic block model, in the case of two classes of equal size, we demonstrate and support with extensive simulations that our proposed algorithm is capable of making non-trivial community reconstruction as soon as theoretically possible, thereby reaching the optimal detectability thresholdand provably outperforming competing spectral methods.

A unified framework for spectral clustering in sparse graphs

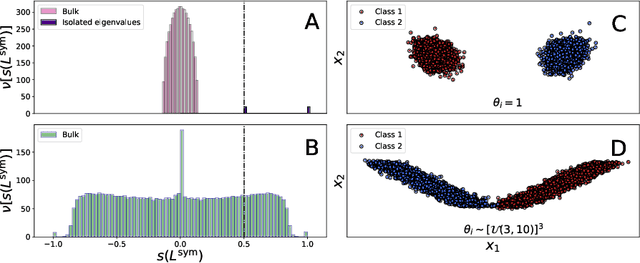
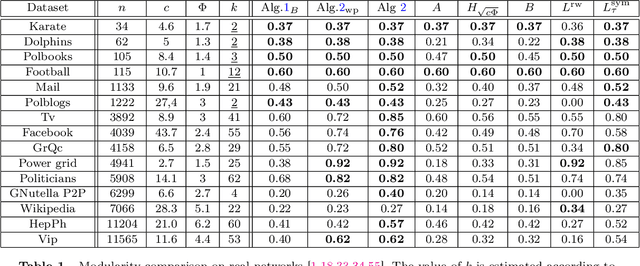
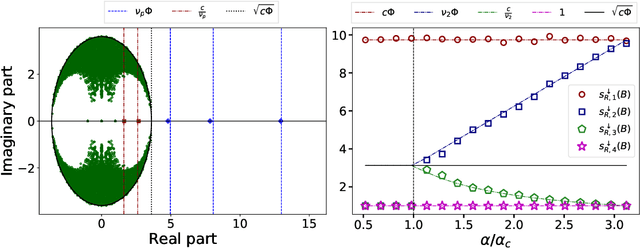
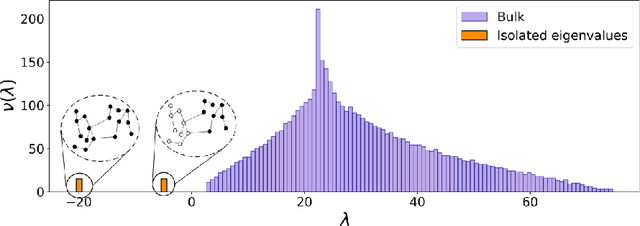
This article considers spectral community detection in the regime of sparse networks with heterogeneous degree distributions, for which we devise an algorithm to efficiently retrieve communities. Specifically, we demonstrate that a conveniently parametrized form of regularized Laplacian matrix can be used to perform spectral clustering in sparse networks, without suffering from its degree heterogeneity. Besides, we exhibit important connections between this proposed matrix and the now popular non-backtracking matrix, the Bethe-Hessian matrix, as well as the standard Laplacian matrix. Interestingly, as opposed to competitive methods, our proposed improved parametrization inherently accounts for the hardness of the classification problem. These findings are summarized under the form of an algorithm capable of both estimating the number of communities and achieving high-quality community reconstruction.

Optimal Laplacian regularization for sparse spectral community detection

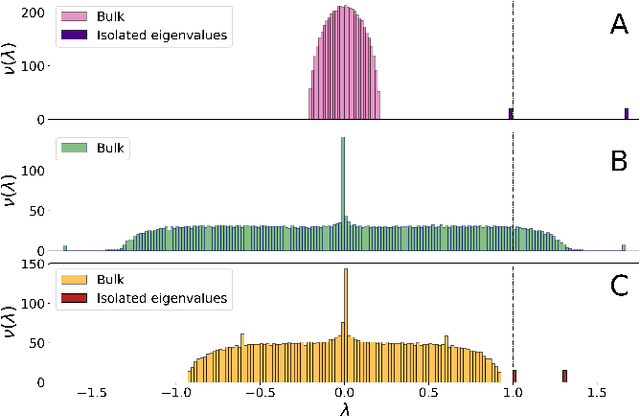
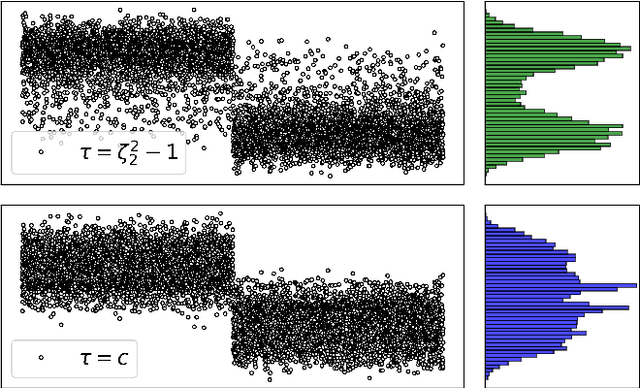
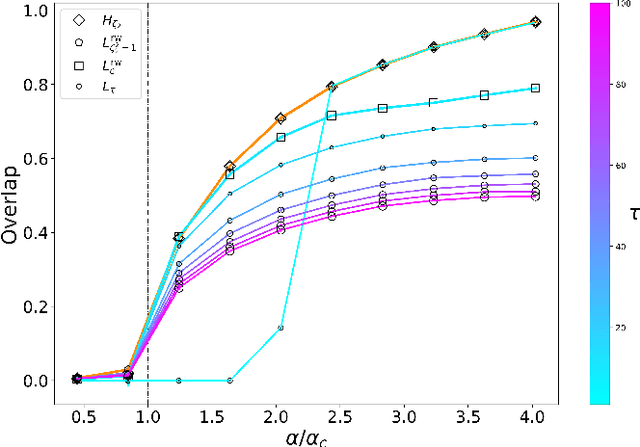
Regularization of the classical Laplacian matrices was empirically shown to improve spectral clustering in sparse networks. It was observed that small regularizations are preferable, but this point was left as a heuristic argument. In this paper we formally determine a proper regularization which is intimately related to alternative state-of-the-art spectral techniques for sparse graphs.

Approximating Spectral Clustering via Sampling: a Review

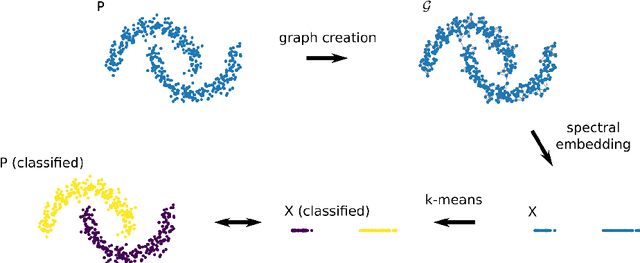
Spectral clustering refers to a family of unsupervised learning algorithms that compute a spectral embedding of the original data based on the eigenvectors of a similarity graph. This non-linear transformation of the data is both the key of these algorithms' success and their Achilles heel: forming a graph and computing its dominant eigenvectors can indeed be computationally prohibitive when dealing with more that a few tens of thousands of points. In this paper, we review the principal research efforts aiming to reduce this computational cost. We focus on methods that come with a theoretical control on the clustering performance and incorporate some form of sampling in their operation. Such methods abound in the machine learning, numerical linear algebra, and graph signal processing literature and, amongst others, include Nystr\"om-approximation, landmarks, coarsening, coresets, and compressive spectral clustering. We present the approximation guarantees available for each and discuss practical merits and limitations. Surprisingly, despite the breadth of the literature explored, we conclude that there is still a gap between theory and practice: the most scalable methods are only intuitively motivated or loosely controlled, whereas those that come with end-to-end guarantees rely on strong assumptions or enable a limited gain of computation time.