Learning Dense 2D-3D Correspondence for X-ray-to-CT Registration of Knee Bones

Recovering the 6-DoF pose of the knee bones from a plain radiograph, given the patient's segmented pre-operative CT, turns a routine low-dose image into a quantitative measurement of joint geometry, without the added dose of a repeat CT or a fixed biplanar rig. Classic solutions align a rendered bone silhouette to image edges; recent alternatives refine pose by backpropagating an image-similarity loss through a differentiable X-ray renderer. Both operate one patient at a time and are fragile under a single view. Silhouettes are depth-ambiguous, and differentiable-rendering refinement has a narrow capture range at substantial per-iteration cost. We instead learn an amortized, subject-agnostic dense 2D-3D correspondence, supervised solely by projection geometry. One shared-weight model per bone, trained across 758 patients, registers patients unseen during training. The pose then follows in closed form from a global, initialization-free, render-free PnP+RANSAC solve. Because X-ray formation is transmissive, our correspondence target is transmission-aware rather than tied to a single surface. Though trained only to register, the representation is anatomically semantic: a simple classifier reads a landmark's anatomical region from its embedding across held-out patients, and the same features separate the knee's bones into a 2D-3D-consistent identity learned without any bone label. On a large single-institution cohort the model generalizes well to held-out patients.

Improved Allergy Wheal Detection for the Skin Prick Automated Test Device

Background: The skin prick test (SPT) is the gold standard for diagnosing sensitization to inhalant allergies. The Skin Prick Automated Test (SPAT) device was designed for increased consistency in test results, and captures 32 images to be jointly used for allergy wheal detection and delineation, which leads to a diagnosis. Materials and Methods: Using SPAT data from $868$ patients with suspected inhalant allergies, we designed an automated method to detect and delineate wheals on these images. To this end, $10,416$ wheals were manually annotated by drawing detailed polygons along the edges. The unique data-modality of the SPAT device, with $32$ images taken under distinct lighting conditions, requires a custom-made approach. Our proposed method consists of two parts: a neural network component that segments the wheals on the pixel level, followed by an algorithmic and interpretable approach for detecting and delineating the wheals. Results: We evaluate the performance of our method on a hold-out validation set of $217$ patients. As a baseline we use a single conventionally lighted image per SPT as input to our method. Conclusion: Using the $32$ SPAT images under various lighting conditions offers a considerably higher accuracy than a single image in conventional, uniform light.

Efficient Training of Neural SDEs Using Stochastic Optimal Control

We present a hierarchical, control theory inspired method for variational inference (VI) for neural stochastic differential equations (SDEs). While VI for neural SDEs is a promising avenue for uncertainty-aware reasoning in time-series, it is computationally challenging due to the iterative nature of maximizing the ELBO. In this work, we propose to decompose the control term into linear and residual non-linear components and derive an optimal control term for linear SDEs, using stochastic optimal control. Modeling the non-linear component by a neural network, we show how to efficiently train neural SDEs without sacrificing their expressive power. Since the linear part of the control term is optimal and does not need to be learned, the training is initialized at a lower cost and we observe faster convergence.

Variational Inference for SDEs Driven by Fractional Noise

We present a novel variational framework for performing inference in (neural) stochastic differential equations (SDEs) driven by Markov-approximate fractional Brownian motion (fBM). SDEs offer a versatile tool for modeling real-world continuous-time dynamic systems with inherent noise and randomness. Combining SDEs with the powerful inference capabilities of variational methods, enables the learning of representative function distributions through stochastic gradient descent. However, conventional SDEs typically assume the underlying noise to follow a Brownian motion (BM), which hinders their ability to capture long-term dependencies. In contrast, fractional Brownian motion (fBM) extends BM to encompass non-Markovian dynamics, but existing methods for inferring fBM parameters are either computationally demanding or statistically inefficient. In this paper, building upon the Markov approximation of fBM, we derive the evidence lower bound essential for efficient variational inference of posterior path measures, drawing from the well-established field of stochastic analysis. Additionally, we provide a closed-form expression to determine optimal approximation coefficients. Furthermore, we propose the use of neural networks to learn the drift, diffusion and control terms within our variational posterior, leading to the variational training of neural-SDEs. In this framework, we also optimize the Hurst index, governing the nature of our fractional noise. Beyond validation on synthetic data, we contribute a novel architecture for variational latent video prediction,-an approach that, to the best of our knowledge, enables the first variational neural-SDE application to video perception.

CenDerNet: Center and Curvature Representations for Render-and-Compare 6D Pose Estimation

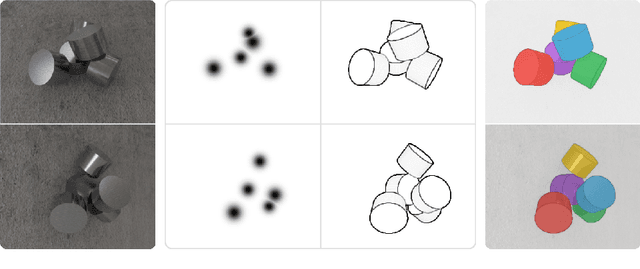
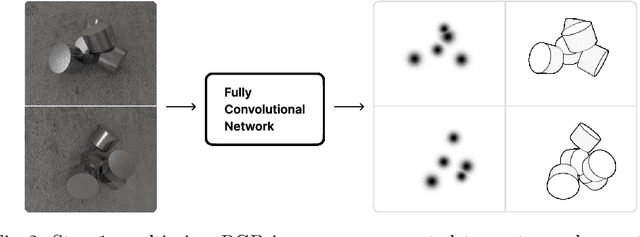
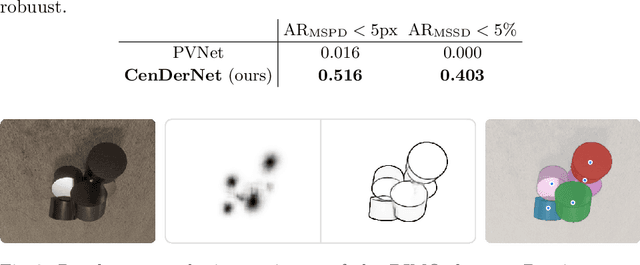
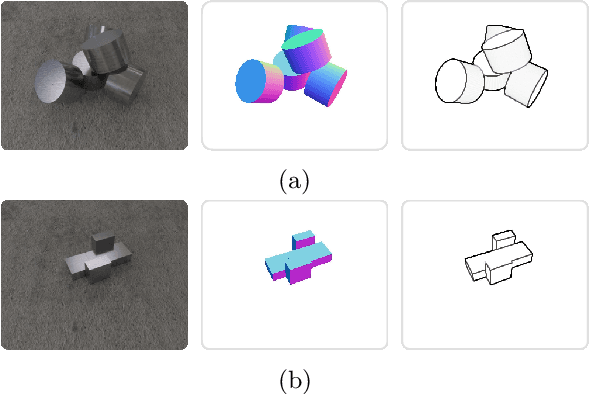
We introduce CenDerNet, a framework for 6D pose estimation from multi-view images based on center and curvature representations. Finding precise poses for reflective, textureless objects is a key challenge for industrial robotics. Our approach consists of three stages: First, a fully convolutional neural network predicts center and curvature heatmaps for each view; Second, center heatmaps are used to detect object instances and find their 3D centers; Third, 6D object poses are estimated using 3D centers and curvature heatmaps. By jointly optimizing poses across views using a render-and-compare approach, our method naturally handles occlusions and object symmetries. We show that CenDerNet outperforms previous methods on two industry-relevant datasets: DIMO and T-LESS.

KeyCLD: Learning Constrained Lagrangian Dynamics in Keypoint Coordinates from Images

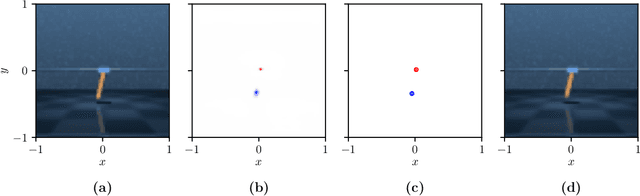
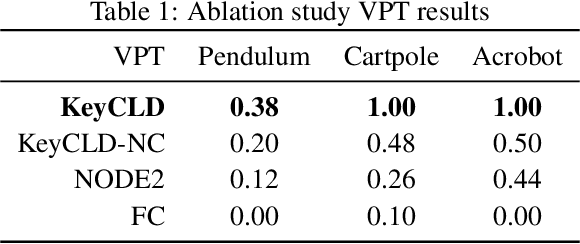
We present KeyCLD, a framework to learn Lagrangian dynamics from images. Learned keypoints represent semantic landmarks in images and can directly represent state dynamics. Interpreting this state as Cartesian coordinates coupled with explicit holonomic constraints, allows expressing the dynamics with a constrained Lagrangian. Our method explicitly models kinetic and potential energy, thus allowing energy based control. We are the first to demonstrate learning of Lagrangian dynamics from images on the dm_control pendulum, cartpole and acrobot environments. This is a step forward towards learning Lagrangian dynamics from real-world images, since previous work in literature was only applied to minimalistic images with monochromatic shapes on empty backgrounds. Please refer to our project page for code and additional results: https://rdaems.github.io/keycld/