Estimating Network Structure from Incomplete Event Data

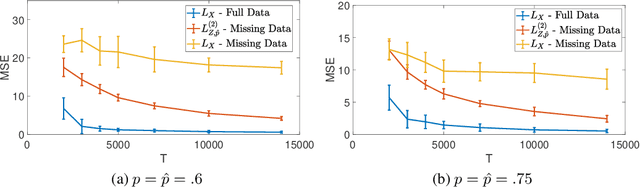
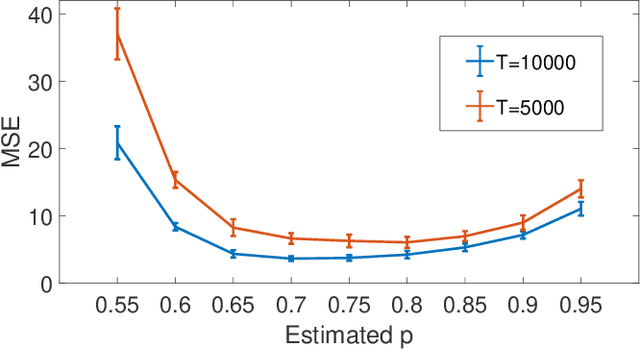
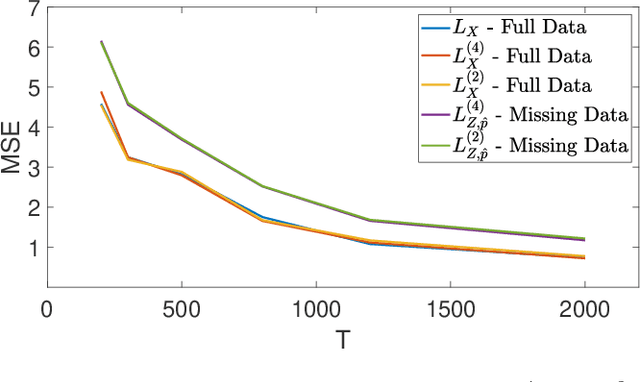
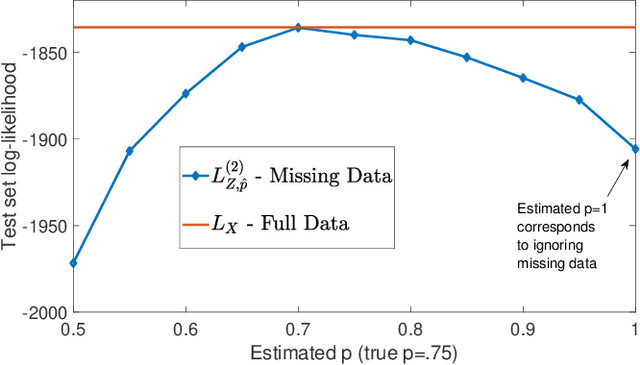
Multivariate Bernoulli autoregressive (BAR) processes model time series of events in which the likelihood of current events is determined by the times and locations of past events. These processes can be used to model nonlinear dynamical systems corresponding to criminal activity, responses of patients to different medical treatment plans, opinion dynamics across social networks, epidemic spread, and more. Past work examines this problem under the assumption that the event data is complete, but in many cases only a fraction of events are observed. Incomplete observations pose a significant challenge in this setting because the unobserved events still govern the underlying dynamical system. In this work, we develop a novel approach to estimating the parameters of a BAR process in the presence of unobserved events via an unbiased estimator of the complete data log-likelihood function. We propose a computationally efficient estimation algorithm which approximates this estimator via Taylor series truncation and establish theoretical results for both the statistical error and optimization error of our algorithm. We further justify our approach by testing our method on both simulated data and a real data set consisting of crimes recorded by the city of Chicago.

Graph-based regularization for regression problems with highly-correlated designs

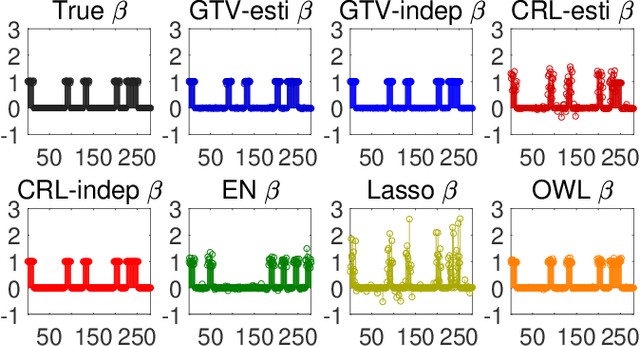
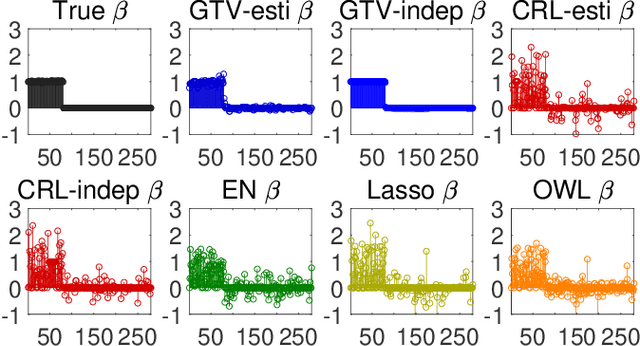
Sparse models for high-dimensional linear regression and machine learning have received substantial attention over the past two decades. Model selection, or determining which features or covariates are the best explanatory variables, is critical to the interpretability of a learned model. Much of the current literature assumes that covariates are only mildly correlated. However, in modern applications ranging from functional MRI to genome-wide association studies, covariates are highly correlated and do not exhibit key properties (such as the restricted eigenvalue condition, RIP, or other related assumptions). This paper considers a high-dimensional regression setting in which a graph governs both correlations among the covariates and the similarity among regression coefficients. Using side information about the strength of correlations among features, we form a graph with edge weights corresponding to pairwise covariances. This graph is used to define a graph total variation regularizer that promotes similar weights for highly correlated features. The graph structure encapsulated by this regularizer helps precondition correlated features to yield provably accurate estimates. Using graph-based regularizers to develop theoretical guarantees for highly-correlated covariates has not been previously examined. This paper shows how our proposed graph-based regularization yields mean-squared error guarantees for a broad range of covariance graph structures and correlation strengths which in many cases are optimal by imposing additional structure on $\beta^{\star}$ which encourages \emph{alignment} with the covariance graph. Our proposed approach outperforms other state-of-the-art methods for highly-correlated design in a variety of experiments on simulated and real fMRI data.

Tensor Methods for Nonlinear Matrix Completion

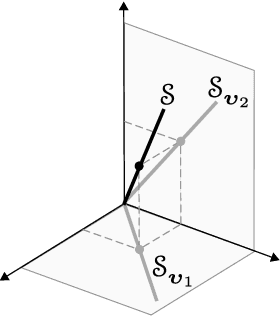
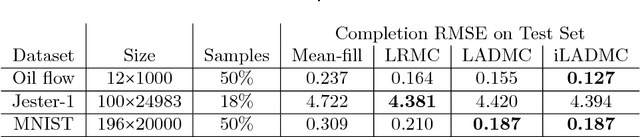
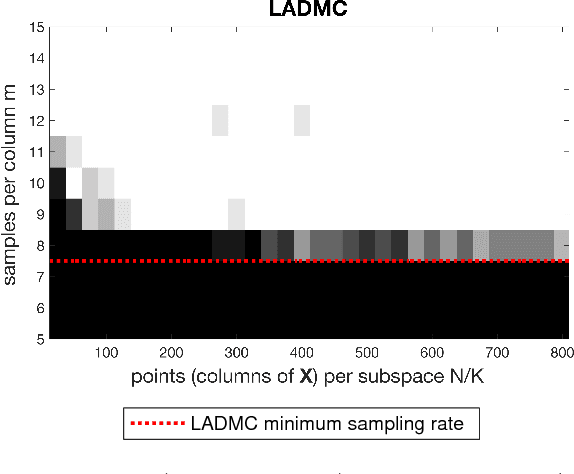
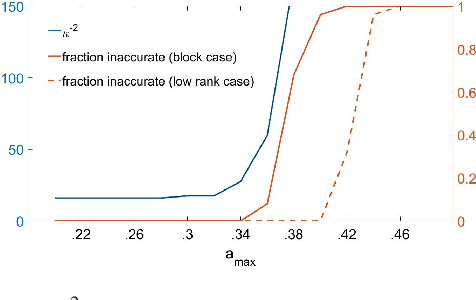
In the low rank matrix completion (LRMC) problem, the low rank assumption means that the columns (or rows) of the matrix to be completed are points on a low-dimensional linear algebraic variety. This paper extends this thinking to cases where the columns are points on a low-dimensional nonlinear algebraic variety, a problem we call Low Algebraic Dimension Matrix Completion (LADMC). Matrices whose columns belong to a union of subspaces (UoS) are an important special case. We propose a LADMC algorithm that leverages existing LRMC methods on a tensorized representation of the data. For example, a second-order tensorization representation is formed by taking the outer product of each column with itself, and we consider higher order tensorizations as well. This approach will succeed in many cases where traditional LRMC is guaranteed to fail because the data are low-rank in the tensorized representation but not in the original representation. We also provide a formal mathematical justification for the success of our method. In particular, we show bounds of the rank of these data in the tensorized representation, and we prove sampling requirements to guarantee uniqueness of the solution. Interestingly, the sampling requirements of our LADMC algorithm nearly match the information theoretic lower bounds for matrix completion under a UoS model. We also provide experimental results showing that the new approach significantly outperforms existing state-of-the-art methods for matrix completion in many situations.

Missing Data in Sparse Transition Matrix Estimation for Sub-Gaussian Vector Autoregressive Processes

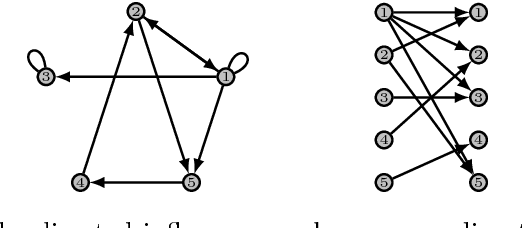
High-dimensional time series data exist in numerous areas such as finance, genomics, healthcare, and neuroscience. An unavoidable aspect of all such datasets is missing data, and dealing with this issue has been an important focus in statistics, control, and machine learning. In this work, we consider a high-dimensional estimation problem where a dynamical system, governed by a stable vector autoregressive model, is randomly and only partially observed at each time point. Our task amounts to estimating the transition matrix, which is assumed to be sparse. In such a scenario, where covariates are highly interdependent and partially missing, new theoretical challenges arise. While transition matrix estimation in vector autoregressive models has been studied previously, the missing data scenario requires separate efforts. Moreover, while transition matrix estimation can be studied from a high-dimensional sparse linear regression perspective, the covariates are highly dependent and existing results on regularized estimation with missing data from i.i.d.~covariates are not applicable. At the heart of our analysis lies 1) a novel concentration result when the innovation noise satisfies the convex concentration property, as well as 2) a new quantity for characterizing the interactions of the time-varying observation process with the underlying dynamical system.

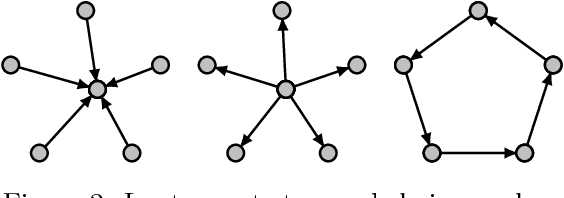
Network Estimation from Point Process Data

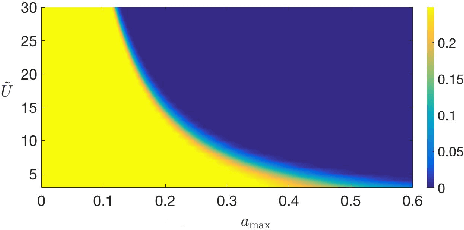
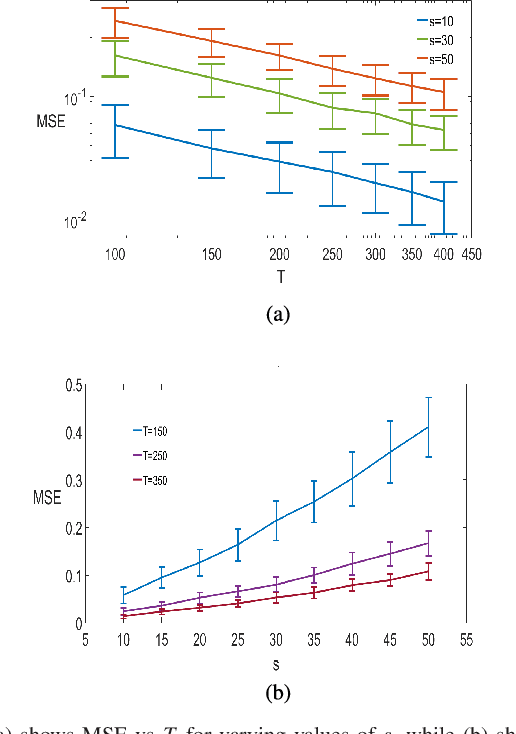
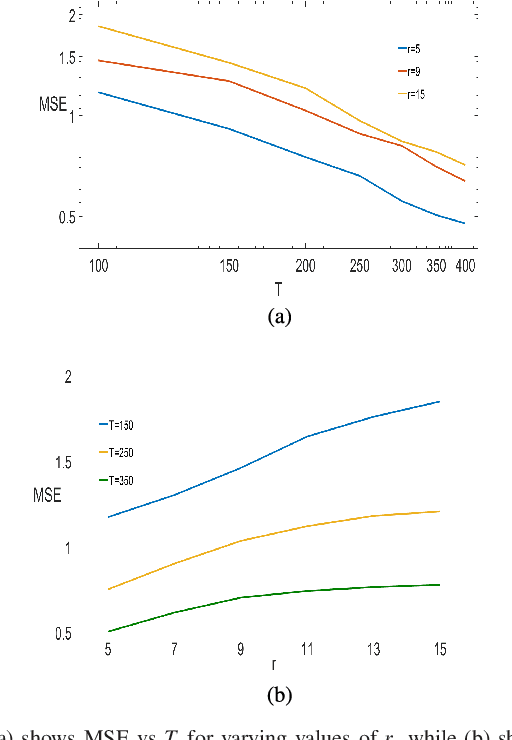
Consider observing a collection of discrete events within a network that reflect how network nodes influence one another. Such data are common in spike trains recorded from biological neural networks, interactions within a social network, and a variety of other settings. Data of this form may be modeled as self-exciting point processes, in which the likelihood of future events depends on the past events. This paper addresses the problem of estimating self-excitation parameters and inferring the underlying functional network structure from self-exciting point process data. Past work in this area was limited by strong assumptions which are addressed by the novel approach here. Specifically, in this paper we (1) incorporate saturation in a point process model which both ensures stability and models non-linear thresholding effects; (2) impose general low-dimensional structural assumptions that include sparsity, group sparsity and low-rankness that allows bounds to be developed in the high-dimensional setting; and (3) incorporate long-range memory effects through moving average and higher-order auto-regressive components. Using our general framework, we provide a number of novel theoretical guarantees for high-dimensional self-exciting point processes that reflect the role played by the underlying network structure and long-term memory. We also provide simulations and real data examples to support our methodology and main results.

Subspace Clustering with Missing and Corrupted Data

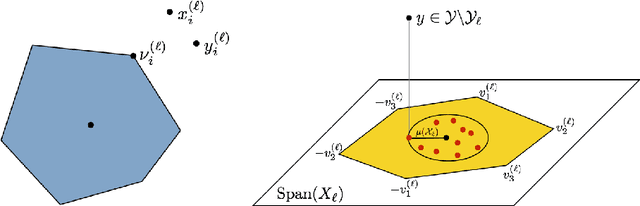
Given full or partial information about a collection of points that lie close to a union of several subspaces, subspace clustering refers to the process of clustering the points according to their subspace and identifying the subspaces. One popular approach, sparse subspace clustering (SSC), represents each sample as a weighted combination of the other samples, with weights of minimal $\ell_1$ norm, and then uses those learned weights to cluster the samples. SSC is stable in settings where each sample is contaminated by a relatively small amount of noise. However, when there is a significant amount of additive noise, or a considerable number of entries are missing, theoretical guarantees are scarce. In this paper, we study a robust variant of SSC and establish clustering guarantees in the presence of corrupted or missing data. We give explicit bounds on amount of noise and missing data that the algorithm can tolerate, both in deterministic settings and in a random generative model. Notably, our approach provides guarantees for higher tolerance to noise and missing data than existing analyses for this method. By design, the results hold even when we do not know the locations of the missing data; e.g., as in presence-only data.

Online Learning for Changing Environments using Coin Betting

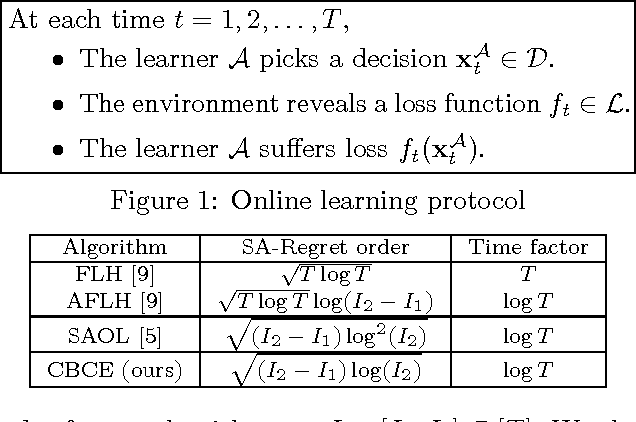
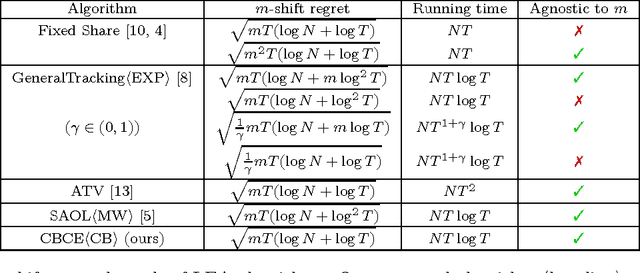
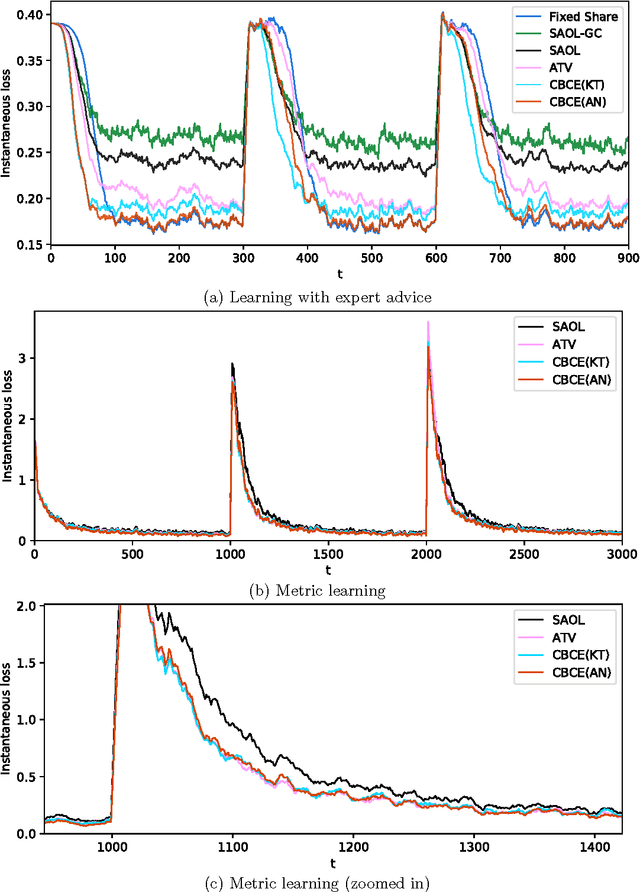
A key challenge in online learning is that classical algorithms can be slow to adapt to changing environments. Recent studies have proposed "meta" algorithms that convert any online learning algorithm to one that is adaptive to changing environments, where the adaptivity is analyzed in a quantity called the strongly-adaptive regret. This paper describes a new meta algorithm that has a strongly-adaptive regret bound that is a factor of $\sqrt{\log(T)}$ better than other algorithms with the same time complexity, where $T$ is the time horizon. We also extend our algorithm to achieve a first-order (i.e., dependent on the observed losses) strongly-adaptive regret bound for the first time, to our knowledge. At its heart is a new parameter-free algorithm for the learning with expert advice (LEA) problem in which experts sometimes do not output advice for consecutive time steps (i.e., \emph{sleeping} experts). This algorithm is derived by a reduction from optimal algorithms for the so-called coin betting problem. Empirical results show that our algorithm outperforms state-of-the-art methods in both learning with expert advice and metric learning scenarios.

Scalable Generalized Linear Bandits: Online Computation and Hashing

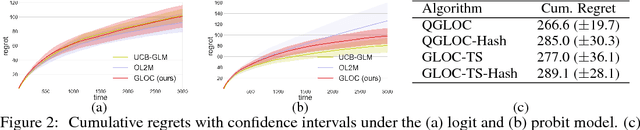
Generalized Linear Bandits (GLBs), a natural extension of the stochastic linear bandits, has been popular and successful in recent years. However, existing GLBs scale poorly with the number of rounds and the number of arms, limiting their utility in practice. This paper proposes new, scalable solutions to the GLB problem in two respects. First, unlike existing GLBs, whose per-time-step space and time complexity grow at least linearly with time $t$, we propose a new algorithm that performs online computations to enjoy a constant space and time complexity. At its heart is a novel Generalized Linear extension of the Online-to-confidence-set Conversion (GLOC method) that takes \emph{any} online learning algorithm and turns it into a GLB algorithm. As a special case, we apply GLOC to the online Newton step algorithm, which results in a low-regret GLB algorithm with much lower time and memory complexity than prior work. Second, for the case where the number $N$ of arms is very large, we propose new algorithms in which each next arm is selected via an inner product search. Such methods can be implemented via hashing algorithms (i.e., "hash-amenable") and result in a time complexity sublinear in $N$. While a Thompson sampling extension of GLOC is hash-amenable, its regret bound for $d$-dimensional arm sets scales with $d^{3/2}$, whereas GLOC's regret bound scales with $d$. Towards closing this gap, we propose a new hash-amenable algorithm whose regret bound scales with $d^{5/4}$. Finally, we propose a fast approximate hash-key computation (inner product) with a better accuracy than the state-of-the-art, which can be of independent interest. We conclude the paper with preliminary experimental results confirming the merits of our methods.

Improved Strongly Adaptive Online Learning using Coin Betting

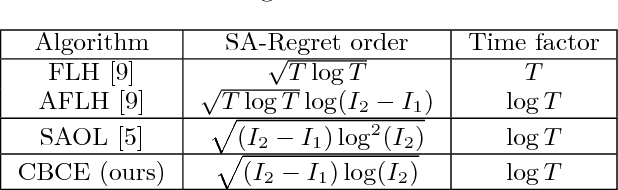
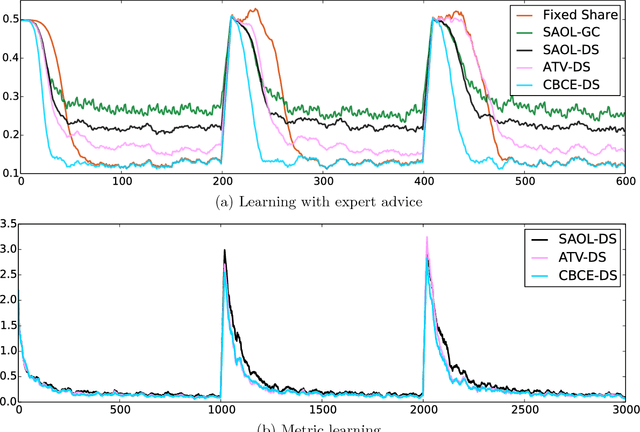
This paper describes a new parameter-free online learning algorithm for changing environments. In comparing against algorithms with the same time complexity as ours, we obtain a strongly adaptive regret bound that is a factor of at least $\sqrt{\log(T)}$ better, where $T$ is the time horizon. Empirical results show that our algorithm outperforms state-of-the-art methods in learning with expert advice and metric learning scenarios.

Inference of High-dimensional Autoregressive Generalized Linear Models

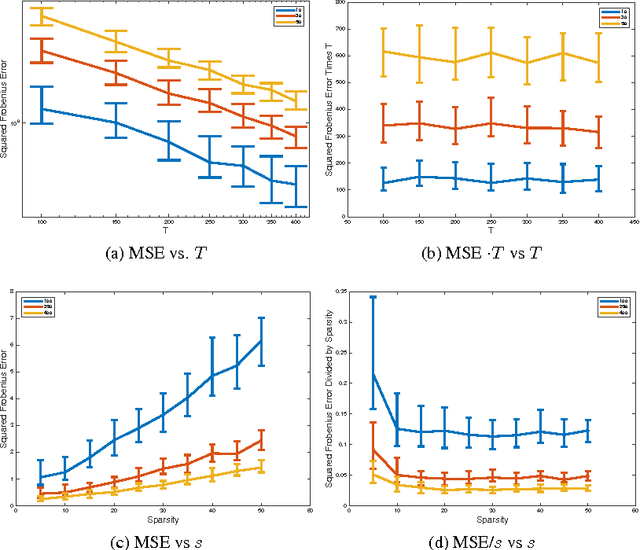
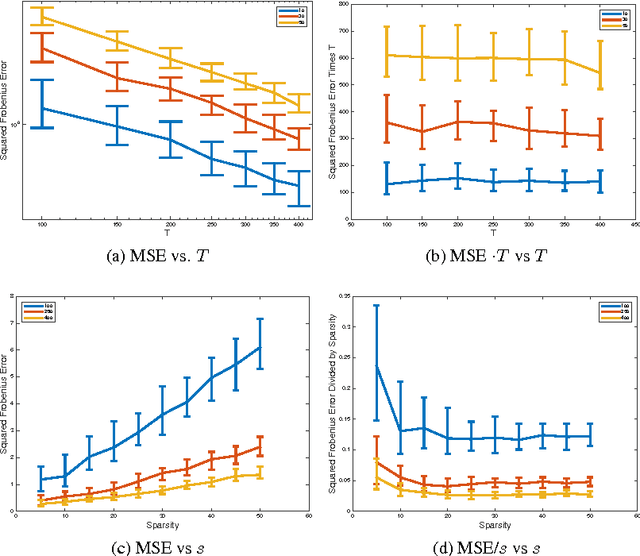
Vector autoregressive models characterize a variety of time series in which linear combinations of current and past observations can be used to accurately predict future observations. For instance, each element of an observation vector could correspond to a different node in a network, and the parameters of an autoregressive model would correspond to the impact of the network structure on the time series evolution. Often these models are used successfully in practice to learn the structure of social, epidemiological, financial, or biological neural networks. However, little is known about statistical guarantees on estimates of such models in non-Gaussian settings. This paper addresses the inference of the autoregressive parameters and associated network structure within a generalized linear model framework that includes Poisson and Bernoulli autoregressive processes. At the heart of this analysis is a sparsity-regularized maximum likelihood estimator. While sparsity-regularization is well-studied in the statistics and machine learning communities, those analysis methods cannot be applied to autoregressive generalized linear models because of the correlations and potential heteroscedasticity inherent in the observations. Sample complexity bounds are derived using a combination of martingale concentration inequalities and modern empirical process techniques for dependent random variables. These bounds, which are supported by several simulation studies, characterize the impact of various network parameters on estimator performance.