Hutch++: Optimal Stochastic Trace Estimation

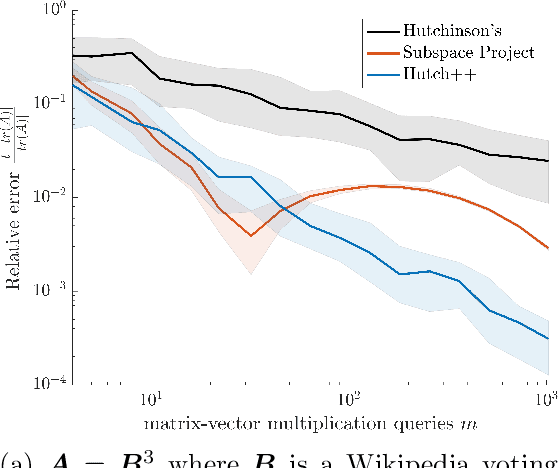
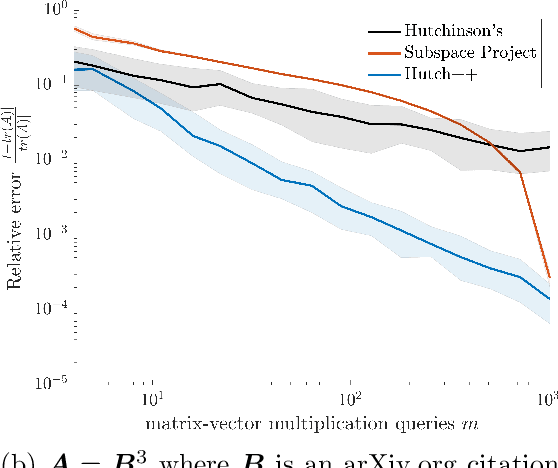
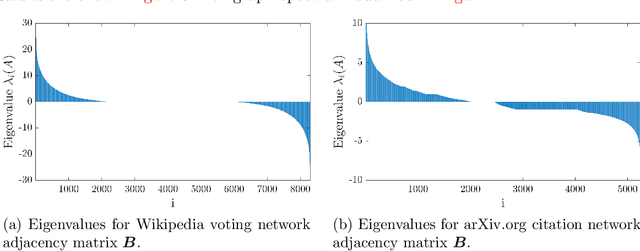
We study the problem of estimating the trace of a matrix $A$ that can only be accessed through matrix-vector multiplication. We introduce a new randomized algorithm, Hutch++, which computes a $(1 \pm \epsilon)$ approximation to $tr(A)$ for any positive semidefinite (PSD) $A$ using just $O(1/\epsilon)$ matrix-vector products. This improves on the ubiquitous Hutchinson's estimator, which requires $O(1/\epsilon^2)$ matrix-vector products. Our approach is based on a simple technique for reducing the variance of Hutchinson's estimator using a low-rank approximation step, and is easy to implement and analyze. Moreover, we prove that, up to a logarithmic factor, the complexity of Hutch++ is optimal amongst all matrix-vector query algorithms, even when queries can be chosen adaptively. We show that it significantly outperforms Hutchinson's method in experiments. While our theory requires $A$ to be positive semidefinite, empirical gains extend to applications involving non-PSD matrices, such as triangle estimation in networks.

The Statistical Cost of Robust Kernel Hyperparameter Tuning

This paper studies the statistical complexity of kernel hyperparameter tuning in the setting of active regression under adversarial noise. We consider the problem of finding the best interpolant from a class of kernels with unknown hyperparameters, assuming only that the noise is square-integrable. We provide finite-sample guarantees for the problem, characterizing how increasing the complexity of the kernel class increases the complexity of learning kernel hyperparameters. For common kernel classes (e.g. squared-exponential kernels with unknown lengthscale), our results show that hyperparameter optimization increases sample complexity by just a logarithmic factor, in comparison to the setting where optimal parameters are known in advance. Our result is based on a subsampling guarantee for linear regression under multiple design matrices, combined with an {\epsilon}-net argument for discretizing kernel parameterizations.