Faster and Space Efficient Indexing for Locality Sensitive Hashing

This work suggests faster and space-efficient index construction algorithms for LSH for Euclidean distance (\textit{a.k.a.}~\ELSH) and cosine similarity (\textit{a.k.a.}~\SRP). The index construction step of these LSHs relies on grouping data points into several bins of hash tables based on their hashcode. To generate an $m$-dimensional hashcode of the $d$-dimensional data point, these LSHs first project the data point onto a $d$-dimensional random Gaussian vector and then discretise the resulting inner product. The time and space complexity of both \ELSH~and \SRP~for computing an $m$-sized hashcode of a $d$-dimensional vector is $O(md)$, which becomes impractical for large values of $m$ and $d$. To overcome this problem, we propose two alternative LSH hashcode generation algorithms both for Euclidean distance and cosine similarity, namely, \CSELSH, \HCSELSH~and \CSSRP, \HCSSRP, respectively. \CSELSH~and \CSSRP~are based on count sketch \cite{count_sketch} and \HCSELSH~and \HCSSRP~utilize higher-order count sketch \cite{shi2019higher}. These proposals significantly reduce the hashcode computation time from $O(md)$ to $O(d)$. Additionally, both \CSELSH~and \CSSRP~reduce the space complexity from $O(md)$ to $O(d)$; ~and \HCSELSH, \HCSSRP~ reduce the space complexity from $O(md)$ to $O(N \sqrt[N]{d})$ respectively, where $N\geq 1$ denotes the size of the input/reshaped tensor. Our proposals are backed by strong mathematical guarantees, and we validate their performance through simulations on various real-world datasets.

Improving LSH via Tensorized Random Projection

Locality sensitive hashing (LSH) is a fundamental algorithmic toolkit used by data scientists for approximate nearest neighbour search problems that have been used extensively in many large scale data processing applications such as near duplicate detection, nearest neighbour search, clustering, etc. In this work, we aim to propose faster and space efficient locality sensitive hash functions for Euclidean distance and cosine similarity for tensor data. Typically, the naive approach for obtaining LSH for tensor data involves first reshaping the tensor into vectors, followed by applying existing LSH methods for vector data $E2LSH$ and $SRP$. However, this approach becomes impractical for higher order tensors because the size of the reshaped vector becomes exponential in the order of the tensor. Consequently, the size of LSH parameters increases exponentially. To address this problem, we suggest two methods for LSH for Euclidean distance and cosine similarity, namely $CP-E2LSH$, $TT-E2LSH$, and $CP-SRP$, $TT-SRP$, respectively, building on $CP$ and tensor train $(TT)$ decompositions techniques. Our approaches are space efficient and can be efficiently applied to low rank $CP$ or $TT$ tensors. We provide a rigorous theoretical analysis of our proposal on their correctness and efficacy.

Improved Outlier Robust Seeding for k-means

The $k$-means is a popular clustering objective, although it is inherently non-robust and sensitive to outliers. Its popular seeding or initialization called $k$-means++ uses $D^{2}$ sampling and comes with a provable $O(\log k)$ approximation guarantee \cite{AV2007}. However, in the presence of adversarial noise or outliers, $D^{2}$ sampling is more likely to pick centers from distant outliers instead of inlier clusters, and therefore its approximation guarantees \textit{w.r.t.} $k$-means solution on inliers, does not hold. Assuming that the outliers constitute a constant fraction of the given data, we propose a simple variant in the $D^2$ sampling distribution, which makes it robust to the outliers. Our algorithm runs in $O(ndk)$ time, outputs $O(k)$ clusters, discards marginally more points than the optimal number of outliers, and comes with a provable $O(1)$ approximation guarantee. Our algorithm can also be modified to output exactly $k$ clusters instead of $O(k)$ clusters, while keeping its running time linear in $n$ and $d$. This is an improvement over previous results for robust $k$-means based on LP relaxation and rounding \cite{Charikar}, \cite{KrishnaswamyLS18} and \textit{robust $k$-means++} \cite{DeshpandeKP20}. Our empirical results show the advantage of our algorithm over $k$-means++~\cite{AV2007}, uniform random seeding, greedy sampling for $k$ means~\cite{tkmeanspp}, and robust $k$-means++~\cite{DeshpandeKP20}, on standard real-world and synthetic data sets used in previous work. Our proposal is easily amenable to scalable, faster, parallel implementations of $k$-means++ \cite{Bahmani,BachemL017} and is of independent interest for coreset constructions in the presence of outliers \cite{feldman2007ptas,langberg2010universal,feldman2011unified}.

Minwise-Independent Permutations with Insertion and Deletion of Features

In their seminal work, Broder \textit{et. al.}~\citep{BroderCFM98} introduces the $\mathrm{minHash}$ algorithm that computes a low-dimensional sketch of high-dimensional binary data that closely approximates pairwise Jaccard similarity. Since its invention, $\mathrm{minHash}$ has been commonly used by practitioners in various big data applications. Further, the data is dynamic in many real-life scenarios, and their feature sets evolve over time. We consider the case when features are dynamically inserted and deleted in the dataset. We note that a naive solution to this problem is to repeatedly recompute $\mathrm{minHash}$ with respect to the updated dimension. However, this is an expensive task as it requires generating fresh random permutations. To the best of our knowledge, no systematic study of $\mathrm{minHash}$ is recorded in the context of dynamic insertion and deletion of features. In this work, we initiate this study and suggest algorithms that make the $\mathrm{minHash}$ sketches adaptable to the dynamic insertion and deletion of features. We show a rigorous theoretical analysis of our algorithms and complement it with extensive experiments on several real-world datasets. Empirically we observe a significant speed-up in the running time while simultaneously offering comparable performance with respect to running $\mathrm{minHash}$ from scratch. Our proposal is efficient, accurate, and easy to implement in practice.

One-pass additive-error subset selection for $\ell_{p}$ subspace approximation

We consider the problem of subset selection for $\ell_{p}$ subspace approximation, that is, to efficiently find a \emph{small} subset of data points such that solving the problem optimally for this subset gives a good approximation to solving the problem optimally for the original input. Previously known subset selection algorithms based on volume sampling and adaptive sampling \cite{DeshpandeV07}, for the general case of $p \in [1, \infty)$, require multiple passes over the data. In this paper, we give a one-pass subset selection with an additive approximation guarantee for $\ell_{p}$ subspace approximation, for any $p \in [1, \infty)$. Earlier subset selection algorithms that give a one-pass multiplicative $(1+\epsilon)$ approximation work under the special cases. Cohen \textit{et al.} \cite{CohenMM17} gives a one-pass subset section that offers multiplicative $(1+\epsilon)$ approximation guarantee for the special case of $\ell_{2}$ subspace approximation. Mahabadi \textit{et al.} \cite{MahabadiRWZ20} gives a one-pass \emph{noisy} subset selection with $(1+\epsilon)$ approximation guarantee for $\ell_{p}$ subspace approximation when $p \in \{1, 2\}$. Our subset selection algorithm gives a weaker, additive approximation guarantee, but it works for any $p \in [1, \infty)$.

Improving \textit{Tug-of-War} sketch using Control-Variates method

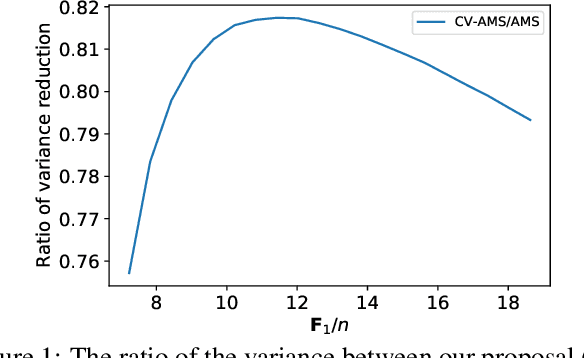
Computing space-efficient summary, or \textit{a.k.a. sketches}, of large data, is a central problem in the streaming algorithm. Such sketches are used to answer \textit{post-hoc} queries in several data analytics tasks. The algorithm for computing sketches typically requires to be fast, accurate, and space-efficient. A fundamental problem in the streaming algorithm framework is that of computing the frequency moments of data streams. The frequency moments of a sequence containing $f_i$ elements of type $i$, are the numbers $\mathbf{F}_k=\sum_{i=1}^n {f_i}^k,$ where $i\in [n]$. This is also called as $\ell_k$ norm of the frequency vector $(f_1, f_2, \ldots f_n).$ Another important problem is to compute the similarity between two data streams by computing the inner product of the corresponding frequency vectors. The seminal work of Alon, Matias, and Szegedy~\cite{AMS}, \textit{a.k.a. Tug-of-war} (or AMS) sketch gives a randomized sublinear space (and linear time) algorithm for computing the frequency moments, and the inner product between two frequency vectors corresponding to the data streams. However, the variance of these estimates typically tends to be large. In this work, we focus on minimizing the variance of these estimates. We use the techniques from the classical Control-Variate method~\cite{Lavenberg} which is primarily known for variance reduction in Monte-Carlo simulations, and as a result, we are able to obtain significant variance reduction, at the cost of a little computational overhead. We present a theoretical analysis of our proposal and complement it with supporting experiments on synthetic as well as real-world datasets.

Dimensionality Reduction for Categorical Data

Categorical attributes are those that can take a discrete set of values, e.g., colours. This work is about compressing vectors over categorical attributes to low-dimension discrete vectors. The current hash-based methods compressing vectors over categorical attributes to low-dimension discrete vectors do not provide any guarantee on the Hamming distances between the compressed representations. Here we present FSketch to create sketches for sparse categorical data and an estimator to estimate the pairwise Hamming distances among the uncompressed data only from their sketches. We claim that these sketches can be used in the usual data mining tasks in place of the original data without compromising the quality of the task. For that, we ensure that the sketches also are categorical, sparse, and the Hamming distance estimates are reasonably precise. Both the sketch construction and the Hamming distance estimation algorithms require just a single-pass; furthermore, changes to a data point can be incorporated into its sketch in an efficient manner. The compressibility depends upon how sparse the data is and is independent of the original dimension -- making our algorithm attractive for many real-life scenarios. Our claims are backed by rigorous theoretical analysis of the properties of FSketch and supplemented by extensive comparative evaluations with related algorithms on some real-world datasets. We show that FSketch is significantly faster, and the accuracy obtained by using its sketches are among the top for the standard unsupervised tasks of RMSE, clustering and similarity search.

Efficient Binary Embedding of Categorical Data using BinSketch

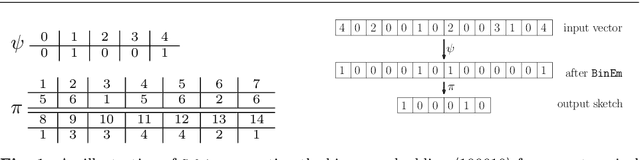
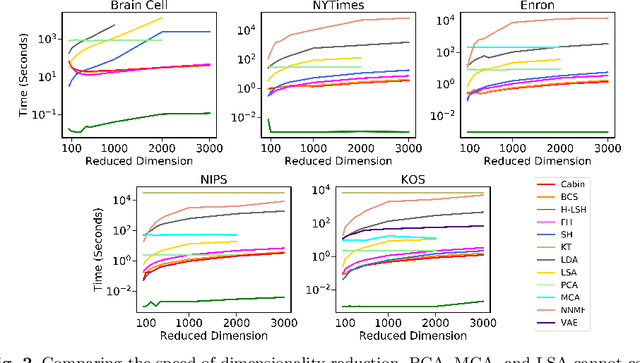
In this work, we present a dimensionality reduction algorithm, aka. sketching, for categorical datasets. Our proposed sketching algorithm Cabin constructs low-dimensional binary sketches from high-dimensional categorical vectors, and our distance estimation algorithm Cham computes a close approximation of the Hamming distance between any two original vectors only from their sketches. The minimum dimension of the sketches required by Cham to ensure a good estimation theoretically depends only on the sparsity of the data points - making it useful for many real-life scenarios involving sparse datasets. We present a rigorous theoretical analysis of our approach and supplement it with extensive experiments on several high-dimensional real-world data sets, including one with over a million dimensions. We show that the Cabin and Cham duo is a significantly fast and accurate approach for tasks such as RMSE, all-pairs similarity, and clustering when compared to working with the full dataset and other dimensionality reduction techniques.

QUINT: Node embedding using network hashing

Representation learning using network embedding has received tremendous attention due to its efficacy to solve downstream tasks. Popular embedding methods (such as deepwalk, node2vec, LINE) are based on a neural architecture, thus unable to scale on large networks both in terms of time and space usage. Recently, we proposed BinSketch, a sketching technique for compressing binary vectors to binary vectors. In this paper, we show how to extend BinSketch and use it for network hashing. Our proposal named QUINT is built upon BinSketch, and it embeds nodes of a sparse network onto a low-dimensional space using simple bi-wise operations. QUINT is the first of its kind that provides tremendous gain in terms of speed and space usage without compromising much on the accuracy of the downstream tasks. Extensive experiments are conducted to compare QUINT with seven state-of-the-art network embedding methods for two end tasks - link prediction and node classification. We observe huge performance gain for QUINT in terms of speedup (up to 7000x) and space saving (up to 80x) due to its bit-wise nature to obtain node embedding. Moreover, QUINT is a consistent top-performer for both the tasks among the baselines across all the datasets. Our empirical observations are backed by rigorous theoretical analysis to justify the effectiveness of QUINT. In particular, we prove that QUINT retains enough structural information which can be used further to approximate many topological properties of networks with high confidence.

On Subspace Approximation and Subset Selection in Fewer Passes by MCMC Sampling

We consider the problem of subset selection for $\ell_{p}$ subspace approximation, i.e., given $n$ points in $d$ dimensions, we need to pick a small, representative subset of the given points such that its span gives $(1+\epsilon)$ approximation to the best $k$-dimensional subspace that minimizes the sum of $p$-th powers of distances of all the points to this subspace. Sampling-based subset selection techniques require adaptive sampling iterations with multiple passes over the data. Matrix sketching techniques give a single-pass $(1+\epsilon)$ approximation for $\ell_{p}$ subspace approximation but require additional passes for subset selection. In this work, we propose an MCMC algorithm to reduce the number of passes required by previous subset selection algorithms based on adaptive sampling. For $p=2$, our algorithm gives subset selection of nearly optimal size in only $2$ passes, whereas the number of passes required in previous work depend on $k$. Our algorithm picks a subset of size $\mathrm{poly}(k/\epsilon)$ that gives $(1+\epsilon)$ approximation to the optimal subspace. The running time of the algorithm is $nd + d~\mathrm{poly}(k/\epsilon)$. We extend our results to the case when outliers are present in the datasets, and suggest a two pass algorithm for the same. Our ideas also extend to give a reduction in the number of passes required by adaptive sampling algorithms for $\ell_{p}$ subspace approximation and subset selection, for $p \geq 2$.